Правильные многогранники

В презентации рассмотрена роль правильных многогранников в философской картине мира. Также представлена космологическая гипотеза Кеплера, в которой он попытался связать некоторые  свойства Солнечной системы со свойствами правильных многогранников.  

Определение:

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер.

Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань

Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработаной великим мыслителем Древней Греции Платоном

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

Тетраэдр - (от греческого tetra – четыре и hedra – грань) - правильный многогранник, составленный из 4 равносторонних треугольников.

Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер.

Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Презентацию выполнила учитель математики МБОУ СОШ №7 пос. Каменномостского Майкопского р-на республики Адыгея

Лукьянченко Людмила Рудольфовна.

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»

Л. Кэрролл

Определение:

• Выпуклый многогранник называется правильным , если все его грани – равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер .

«В огромном саду геометрии каждый найдет букет себе по вкусу.»

Д. Гильберт

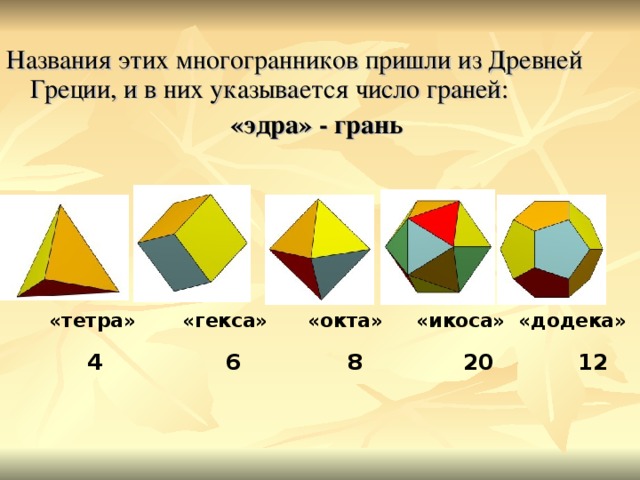
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:

«эдра» - грань

«тетра» «гекса» «окта» «икоса» «додека»

4 6 8 20 12

4

Платон (ок. 428 – ок. 348 до н.э.)

Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработан-

великим мыслителем Древней Греции Платоном

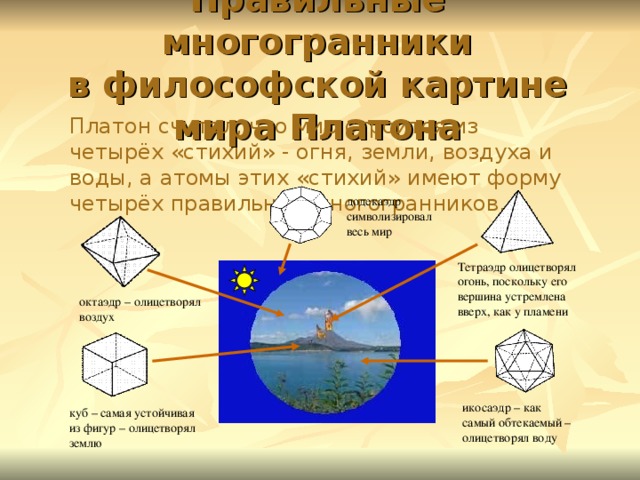
Правильные многогранники в философской картине мира Платона

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

додекаэдр символизировал весь мир

Тетраэдр олицетворял огонь, поскольку его вершина устремлена

вверх, как у пламени

октаэдр – олицетворял воздух

икосаэдр – как самый обтекаемый – олицетворял воду

куб – самая устойчивая из фигур – олицетворял землю

Тетраэдр   (от греческого tetra – четыре и hedra – грань) - правильный многогранник, составленный из 4 равносторонних треугольников.

Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер.

Сумма длин всех

ребер

Площадь

поверхности

тетраэдра

Объем

Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.

Радиус описанной

сферы

Радиус вписанной

сферы

8

Куб (гексаэдр)   (от греческого hex — шесть и hedra — грань) - правильный многогранник, составленный из 6 квадратов.

Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят  9 осей симметрии .

Сумма длин всех

ребер

Площадь

поверхности

тетраэдра

Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра ( таковых плоскостей 6), либо через середины противоположных ребер (таких - 3).

Объем

Радиус описанной

сферы

Радиус вписанной

сферы

9

Октаэдр ( от греческого okto – восемьи hedra – грань) –правильный многогранник, составленный из 8 равносторонних треугольников.

Октаэдр обладает симметрией.   Три из 9 осей симметрии октаэдра проходят через противоположные вершины, шесть - через середины ребер. Центр симметрии октаэдра - точка пересечения его осей симметрии.

Сумма длин всех

ребер

Площадь

поверхности

тетраэдра

Объем

Три из 9 плоскостей симметрии тетраэдра проходят через каждые 4   вершины октаэдра,   лежащие в одной плоскости . Шесть  плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер.

Радиус описанной

сферы

Радиус вписанной

сферы

10

Додекаэдр

( от греческого dodeka – двенадцать и hedra – грань) – это правильный многогранник,  составленный из двенадцати равносторонних пятиугольников.

Сумма длин всех

ребер

Площадь

поверхности

тетраэдра

Объем

Плоскостей симметрии 9 и проходят они либо через противоположные ребра

(таковых плоскостей 6), либо через середины противоположных ребер (таких - 3). Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.

Радиус описанной

сферы

Радиус вписанной

сферы

Икосаэдр

(от греческого ico —  шесть и hedra — грань) правильный

выпуклый многогранник, составленный из 20 правильных треугольников.

Сумма длин всех

ребер

Площадь

поверхности

тетраэдра

Объем

Правильный икосаэдр имеет 15 осей симметрии , каждая из  которых  проходит через  середины противоположных параллельных  ребер.

Плоскостей симметрии также 15 .

.

Радиус описанной

сферы

Радиус вписанной

сферы

Совершенство и гармония многогранников поражает скульпторов, архитекторов, художников.

Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.

12

Совершенство и гармония многогранников поражает скульпторов, архитекторов, художников.

Сальвадор Дали на картине «Тайная вечеря» изобразил Иисуса Христа со своими учениками на фоне огромного прозрачного додекаэдра

12

Иоганн Кеплер (1571 – 1630 гг.)

Немецкий астроном и математик. Один из создателей современной астрономии.

Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках.

Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.

Космологическая гипотеза Кеплера

Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.

Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел.

• Литература:

• Винниджер. Модели многогранников. М., 1975.
• Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кардомцев и др.–5-е изд.– М.: Просвещение, 2000.
• Гросман С., Тернер Дж. Математика для биологов. М., 1983.
• Кованцов Н.И. Математика и романтика. Киев, 1976.
• Смирнова И.М. В мире многогранников. М., 1990.
• Шафрановский И.И. Симметрия в природе. Л., 1988.

• Web - ресурсы:

• http://dr-klm.livejournal.com/117917.html
• http://polyhedron.boom.ru/pages/tetra.htm