Нахождение производных
Правила дифференцирования
Пусть u=u(x), v=v(x), w=w(x) – некоторые функции, с – некоторое число, тогда:
(с·u)`=c·u`(постоянный множитель можно выносить за знак производной);
(u+v-w)`=u`+v`-w`(производная суммы (разности) функций равна сумме (разности) производных этих функций);
(u·v)`=u`·v+u·v`(производная произведения);
Весь материал - смотрите документ.
Нахождение производных
Правила дифференцирования
Пусть u=u(x), v=v(x), w=w(x) – некоторые функции, с – некоторое число, тогда:
(с·u)`=c·u`(постоянный множитель можно выносить за знак производной);
(u+v-w)`=u`+v`-w`(производная суммы (разности) функций равна сумме (разности) производных этих функций);
(u·v)`=u`·v+u·v`(производная произведения);
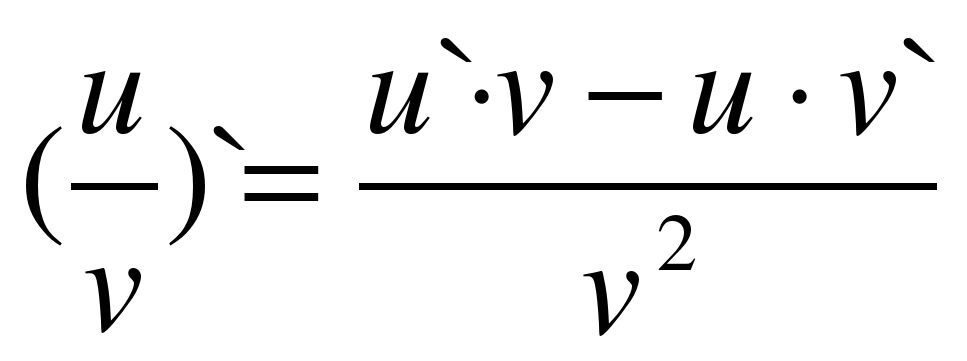(производная частного).
Формулы дифференцирования (таблица производных)
| № | Простые функции y=f(x) | Сложные функции y=f(u), где u=u(x) |
| 1 | c`=0 |
|
| 2 | x`=1 |
|
| 3 | (kx+b)`=k |
|
| 4 |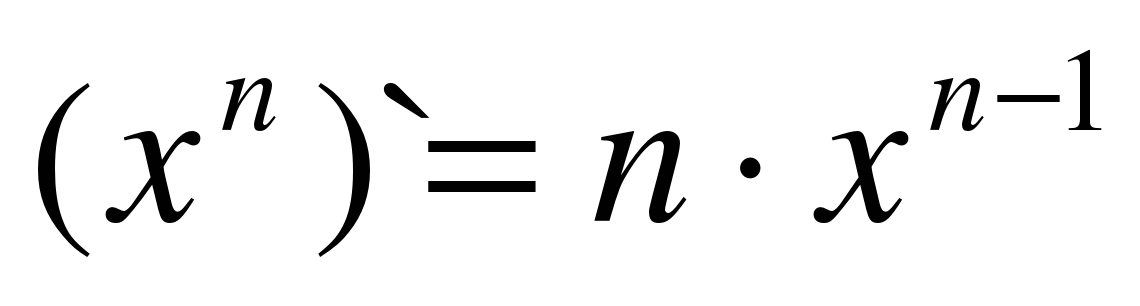
|
|
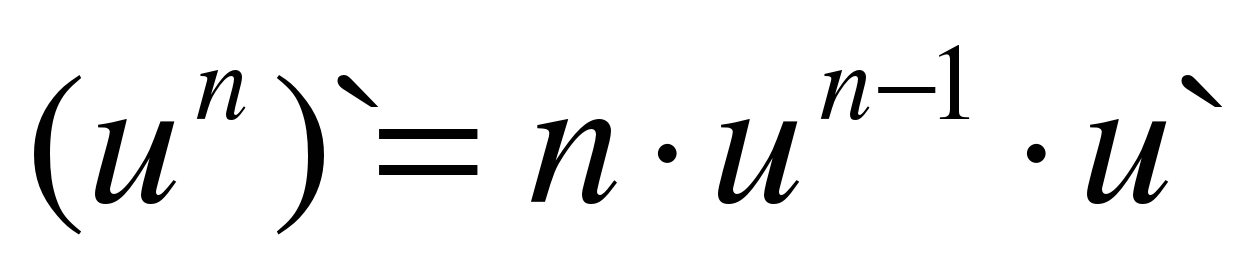
| 5 |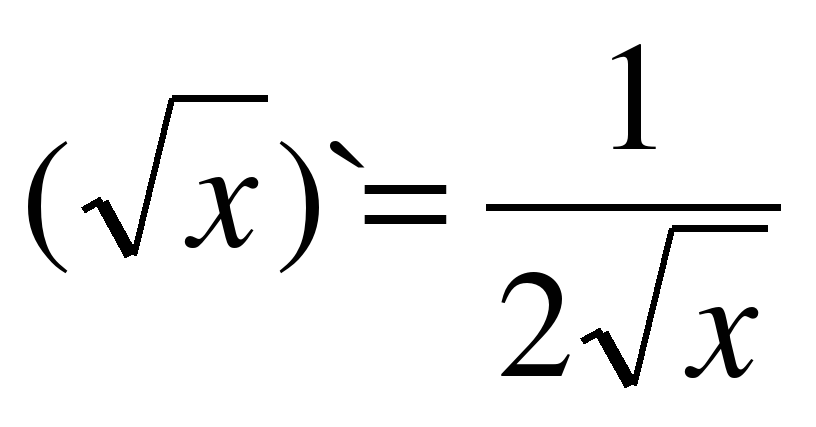
|
|
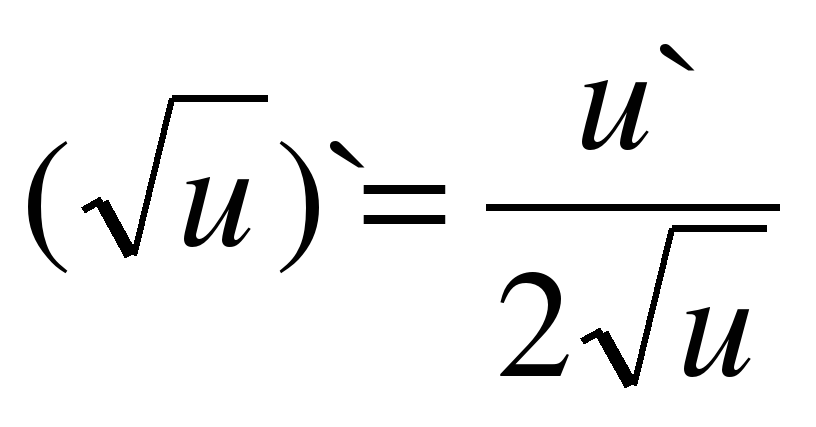
| 6 |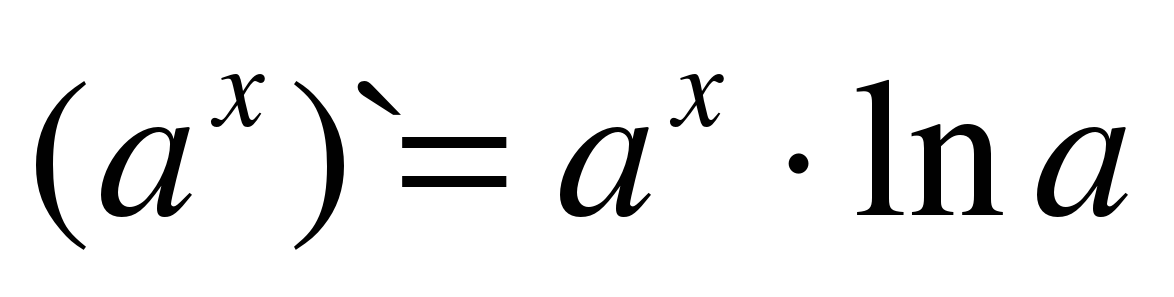
|
|
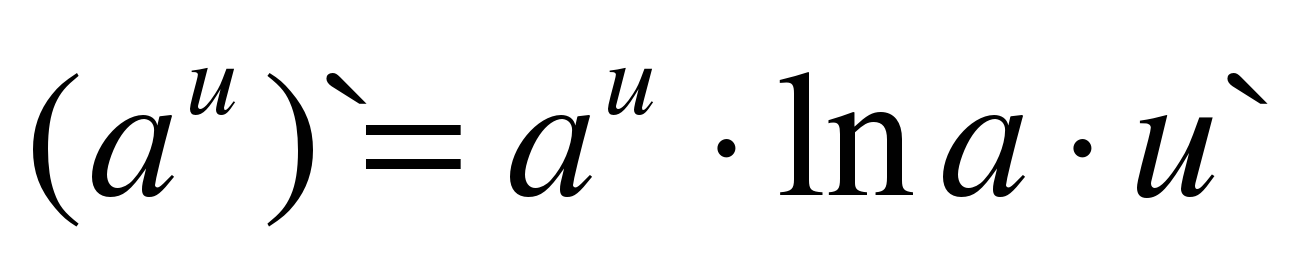
| 7 |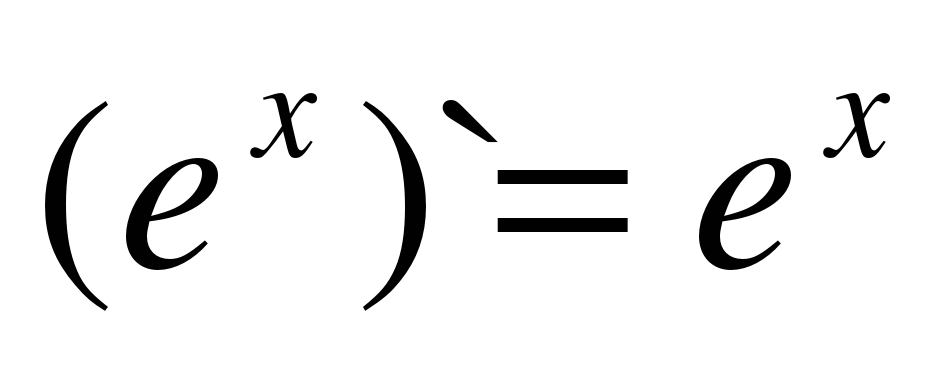
|
|
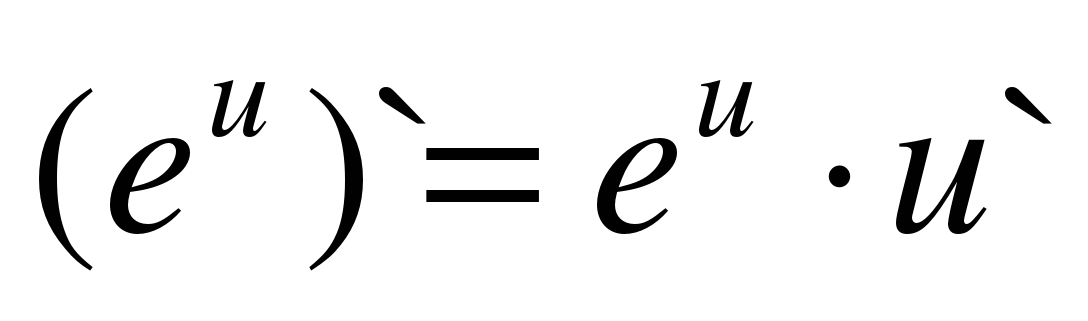
| 8 |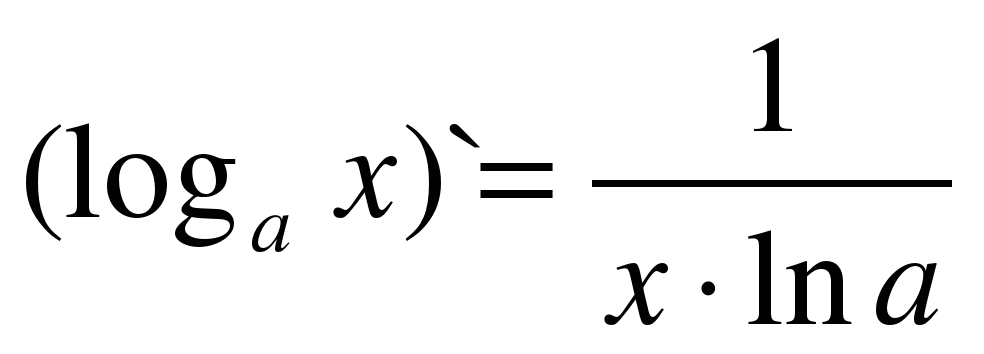
|
|
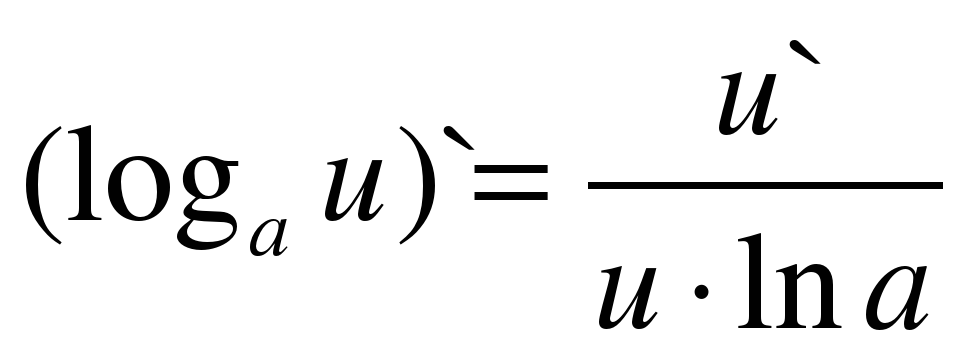
| 9 |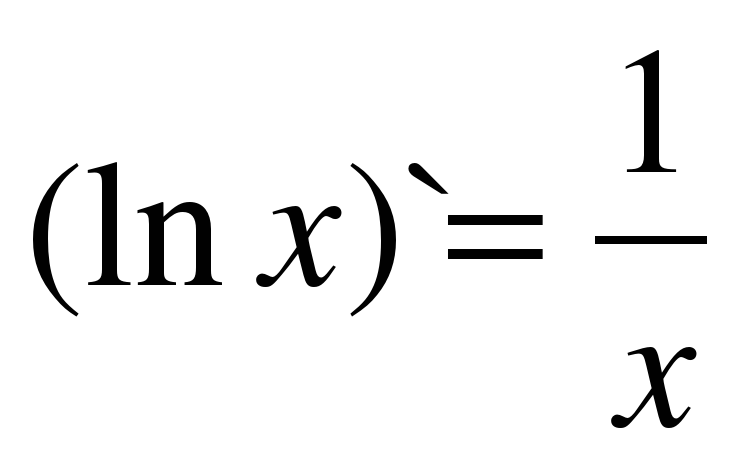
|
|
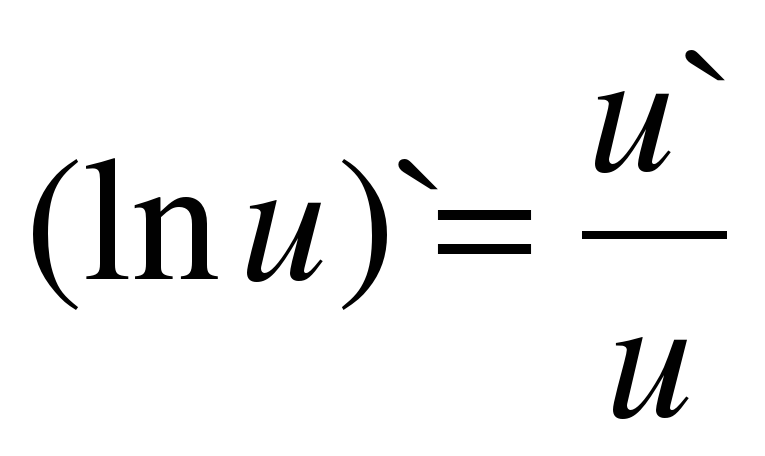
| 10 | (sin x)`= cos x | (sin u)`= cos u·u` |
| 11 | (cos x)`= - sin x | (cos u)`= - sin u·u` |
| 12 |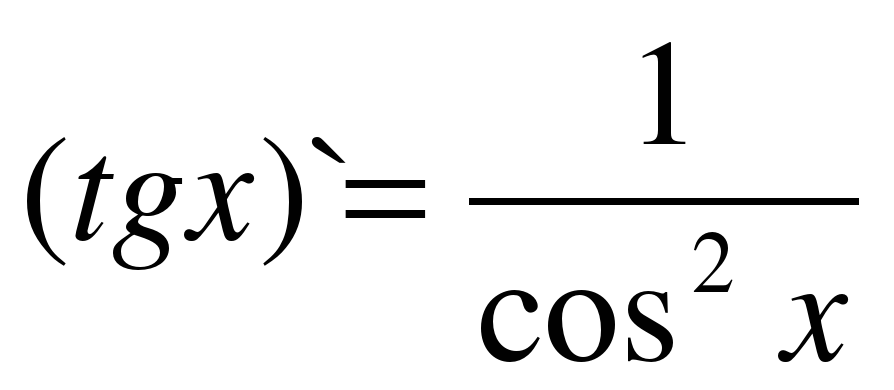
|
|
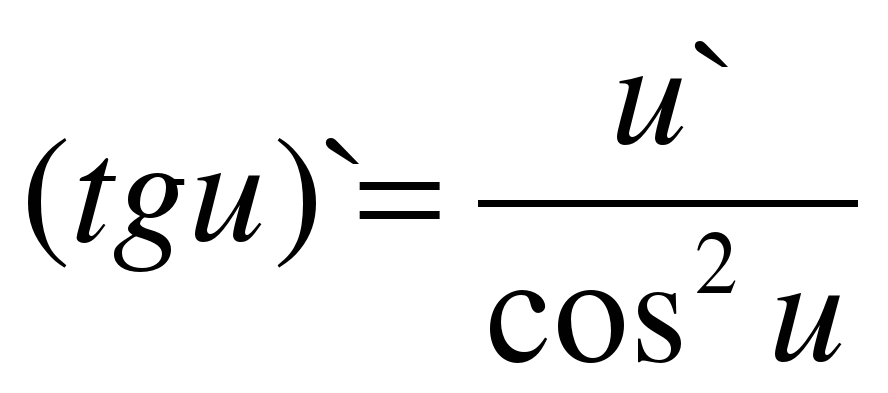
| 13 |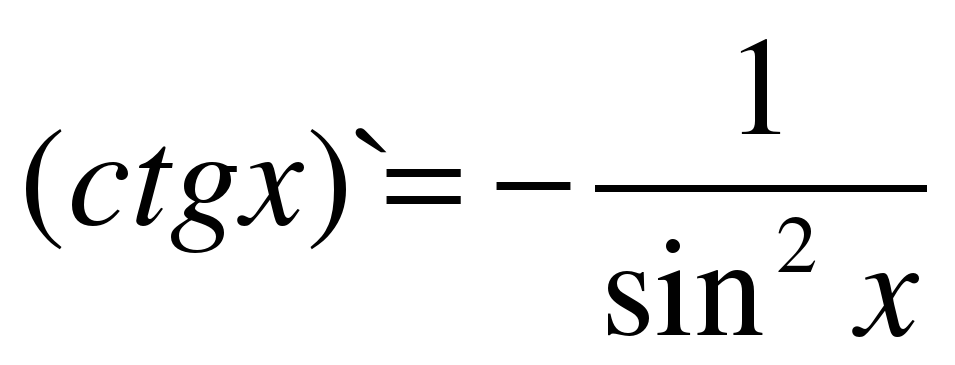
|
|
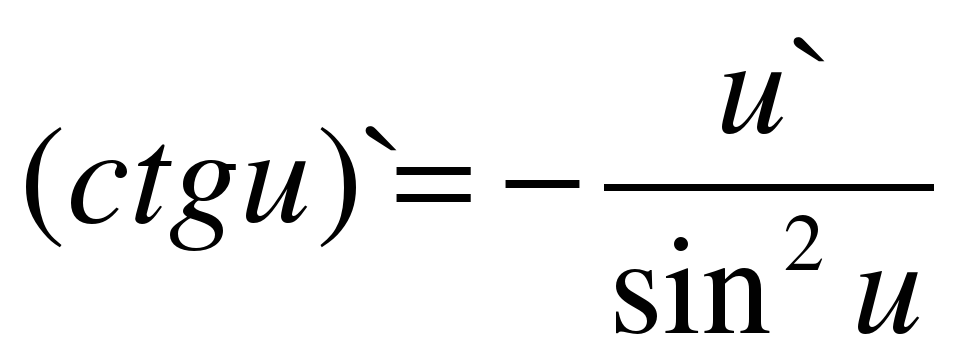
| 14 |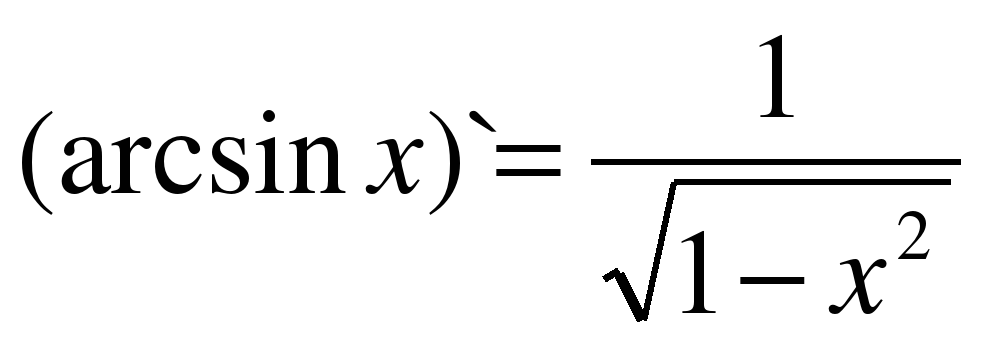
|
|
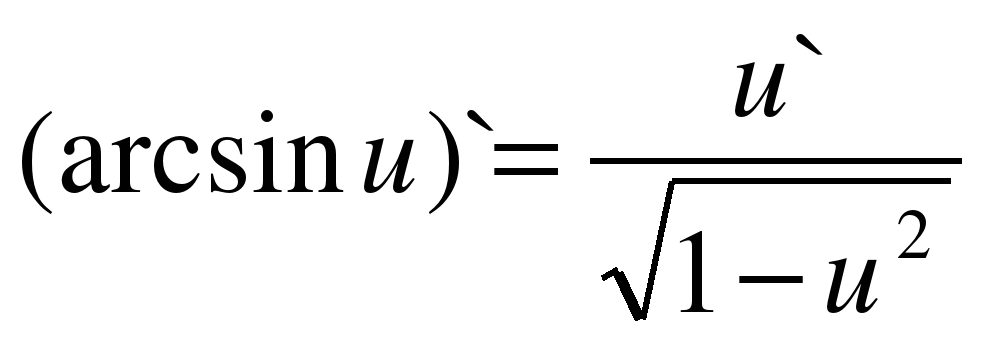
| 15 |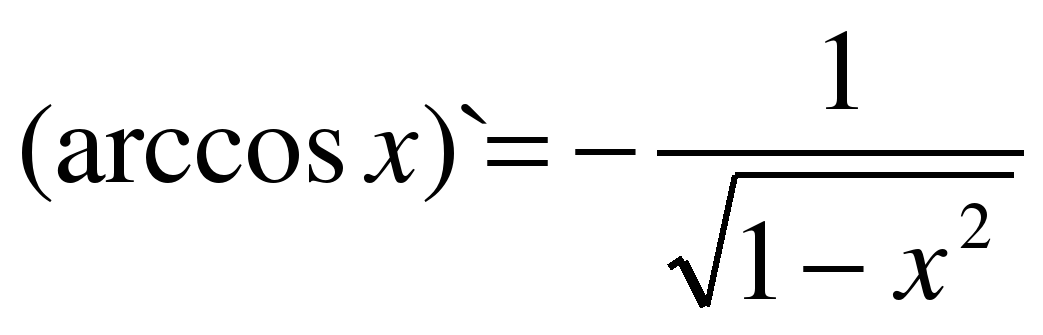
|
|
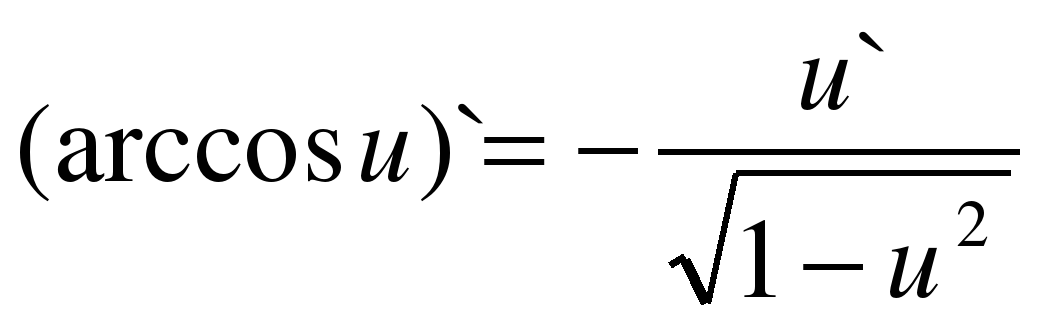
| 16 |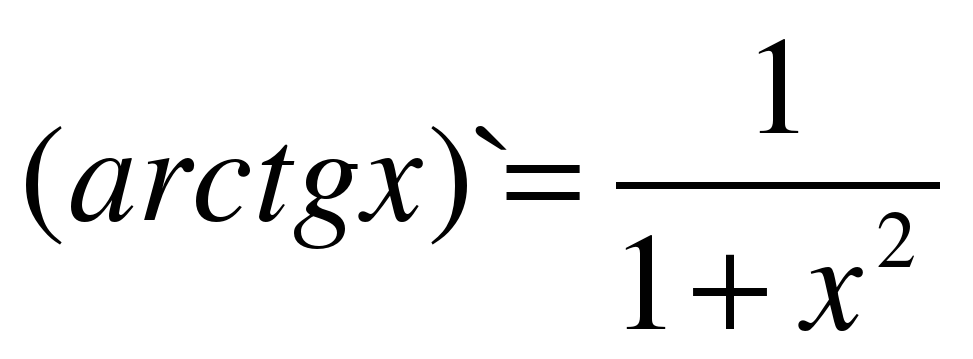
|
|
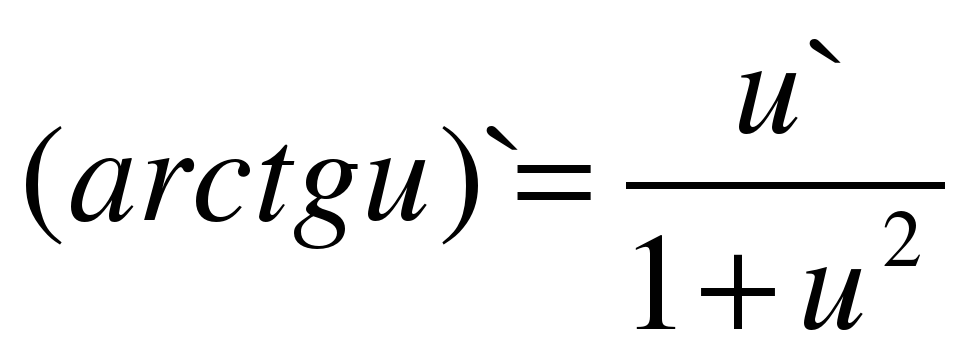
| 17 |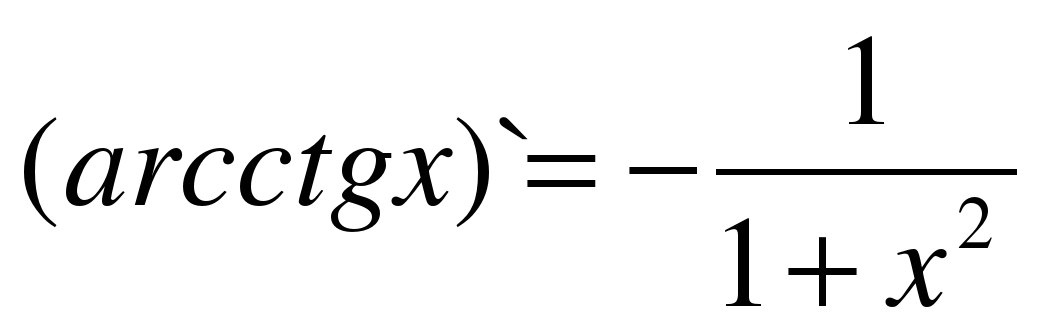
|
|
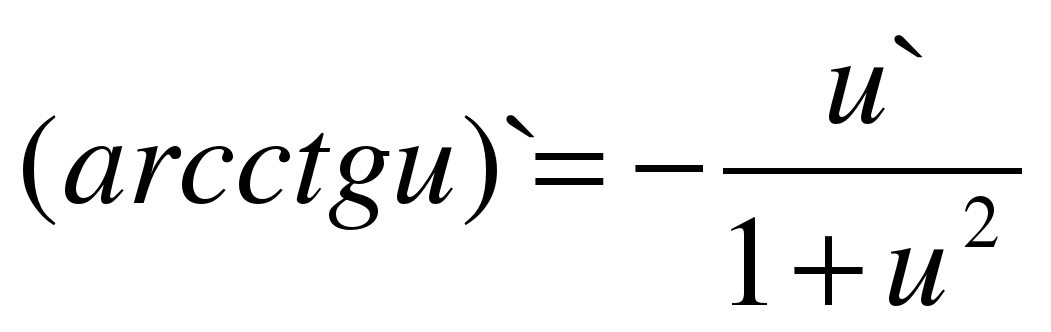
Нахождение неопределенных интегралов
Правила интегрирования
Пусть u = u(x), v = v(x), w = w(x) – некоторые функции, k – некоторое число, тогда:
1)
(постоянный множитель можно выносить за знак неопределенного интеграла);
2)
(неопределенный интеграл суммы (разности) функций равен сумме (разности) неопределенных интегралов этих функций).
Формулы интегрирования (таблица интегралов)
| № | Простые функции y=f(x) | Сложные функции y=f(u), где u=kx+b, k и b – некоторые числа (k ≠ 0) |
| 1 | , В частности, при n=0: | , |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
-80%
0
6018
125
Нравится
1
Получите свидетельство
Вход
Правила и формулы дифференцирования и интегрирования (0.14 MB)
