Получите свидетельство
Вход
Тема урока: Правильные многогранники.
Тип урока: Изучение новых знаний и способов действий.
Цель урока: Раскрыть сущность создать и организовать условия для осмысления и усвоения учебной информации по теме: «Правильные многогранники», организовать деятельность учащихся по открытию нового знания.
Задачи урока:
Предметные
формирование представления о правильных многогранниках;
умение определять тип многогранника по его внешнему виду;
умение определять количество ребер вершин и граней многогранника, использовать формулу Эйлера.
Метапредметные
развитие умения генерировать идеи, выявлять причинно-следственные связи, искать аналогии и работать в команде;
формировать умение анализировать факты при работе с текстом учебника.
Личностные
понимание значения использования различных многогранников в жизни человека;
формирование мотивации постановкой познавательных задач, раскрытием связи теории и опыта,
развитие наблюдательности, внимания, логического мышления, интереса к изучению математики.
Формируемые УУД:
Познавательные
- анализировать, синтезировать;
- использовать знаково - символические средства;
Регулятивные
- прогнозировать предстоящую работу;
- планировать свою деятельность, используя алгоритм;
- выполнять само- и взаимооценку при выполнении учебного задания;
- выполнять самоанализ своей деятельности.
Коммуникативные
- строить понятные для партнера высказывания;
- адекватно взаимодействовать в паре и группе при выполнении учебного задания;
Личностные
- умение грамотно говорить и легко выражать свои мысли;
- умение работать в группе;
- развитие чувства взаимовыручки;
- расширение кругозора.
Формы организации познавательной деятельности обучающихся: коллективная, индивидуальная, групповая.
Методы организации познавательной деятельности обучающихся: технология критического мышления, методы проблемного обучения: частично-поисковые или эвристические; практические методы освоения материала.
Используемые на уроке средства ИКТ:
персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
УМК Муравина, Математика 6 класс, рабочая тетрадь, ножницы, бумага, развертки правильных многогранников.
презентация «Правильные многогранники».
Этапы урока.
Организационный момент.
Мотивация.
Изучение нового материала.
Первичное закрепление изученного.
Практическая работа.
Итог урока.
Домашнее задание.
Этап рефлексии учебной деятельности на уроке.
Ход урока.
| Деятельность учителя | Деятельность учащихся |
| I. Организационный момент. | |
| Приветствие. Проверка присутствующих. | Подготовка к уроку. |
| II. Мотивация | |
| - Сегодня мы пойдем в гости к геммологам. Знаете ли вы кто это? (Слайд 1)
- Можно ли эти кристаллы назвать геометрическими телами? К какому виду геометрических тел их можно отнести: многогранникам или телам вращения? Проблемная ситуация. Посмотрите на их грани. Что в них особенного? Как называют такие многогранники? | Выясняется, что ученики не знают что это такое.
Отвечают на вопросы: Да. Многогранникам.
Грани представляют собой правильные треугольники. Правильными. |
| - Тема нашего урока «Правильные многогранники» (Слайд 2). - На сегодняшнем уроке мы: Выясним сколько всего существует правильных многогранников и как они называются. Где в природе мы можем встретить многогранники. Многогранники… но причем здесь математик Леонард Эйлер? Сделаем из бумаги правильные многогранники, используя их развертку (Слайд 3).
- Запишите тему нашего урока. | Записывают тему урока в тетрадь. |
| III. Изучение нового материала. | |
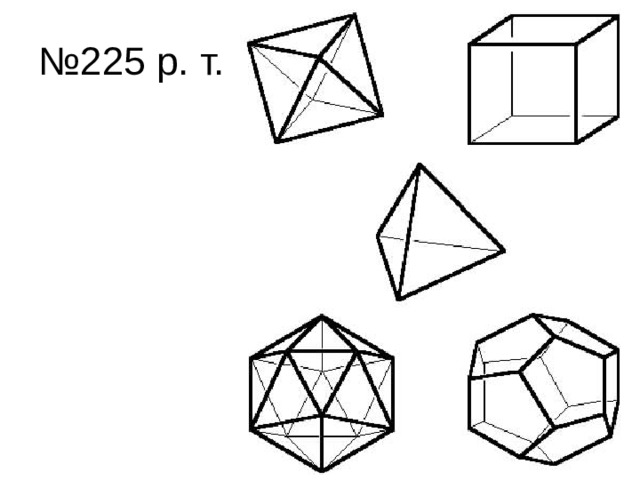
| Самостоятельная работа с материалом учебника стр. 215. (Слайды 4 – 8).
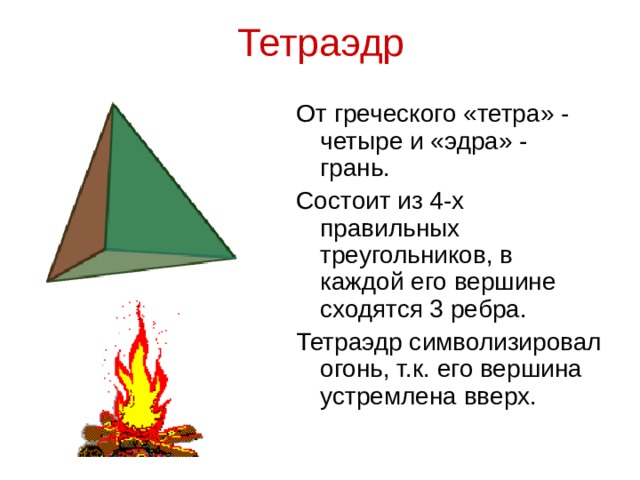
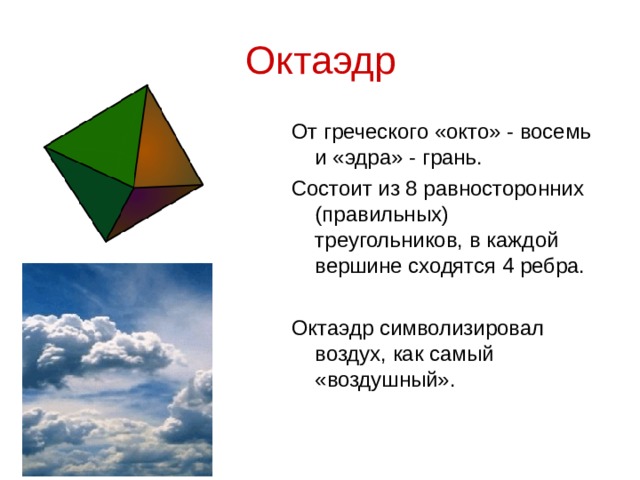
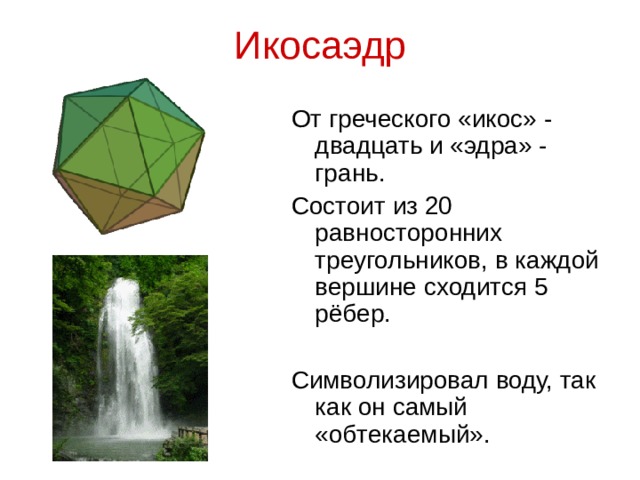
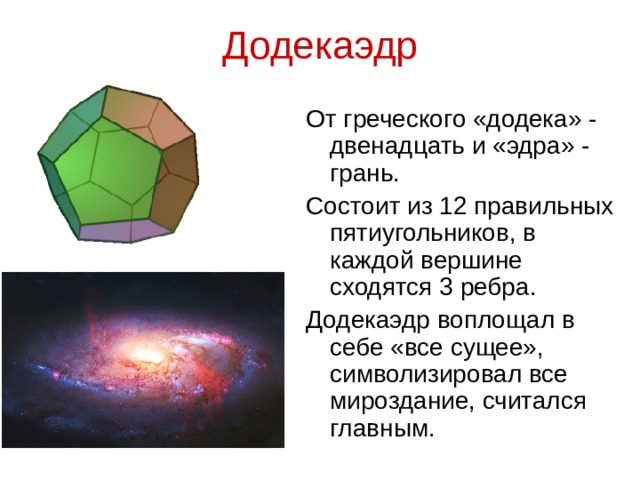
Несколько учеников готовят сообщение о правильных многогранниках в природе и жизни человека (Слайды 9-10). | Ученики читают материал, а затем рассказывают о каждом многограннике у доски.
Чтобы найти нужную информацию удобнее всего воспользоваться Интернетом. |
| IV. Первичное закрепление изученного. | |
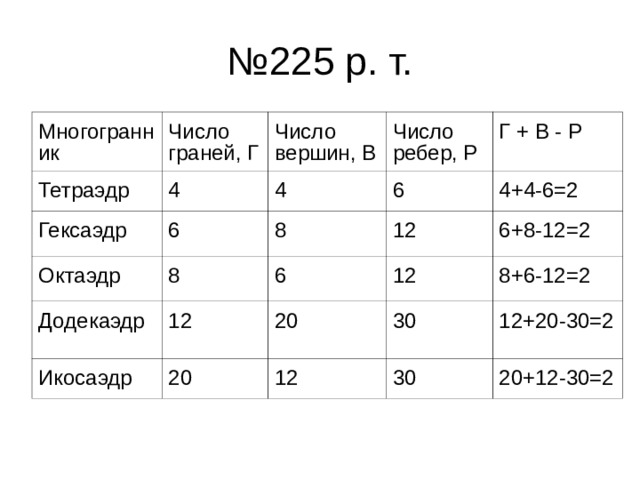
| № 255 р. т.
Самостоятельная работа в парах с последующей самопроверкой. (Слайд 11). - Какую закономерность мы выявили? (Слайд 12) | Первая строчка таблицы заполняется вместе с учителем. Выполняют самостоятельную работу. Осуществляют самопроверку и выставляют себе оценки. Записывают формулу Эйлера в тетрадь.
|
| V. Практическая работа. | |
| Практическая работа. Работа в группах.
| Ученики делятся на 6 групп. Каждая группа по развертке склеивает свой правильный многогранник. Дает ему название. |
| VI. Итог урока. | |
| Возвращение к теме и целям урока. - Какова была цель нашего урока? - Достигли ли мы цели?
| Каждая группа оценивает свою деятельность: дружно ли работали, кто работал хуже, все ли получилось, что вызвало затруднения. |
| VII. Домашнее задание. | |
| 1) Стр. 215 читать, выучить названия правильных многогранников. 2) №690, 691, (дополнительно №701). 3) Творческие задания. | Записывают домашнее задание. |
| VIII. Рефлексия. | |
| Продолжите предложение: - Особенно мне понравилось … - Мне было интересно … - Для меня было новым … - Мне и раньше было известно … - Наибольшее затруднение вызвало … - Мне следует ещё поработать над …
Поощрение команд, и более активных участников, выставление оценок. | Ученики отвечают на вопросы. |
Правильные многогранники (2.88 MB)
0
421
16
Нравится
0
