Практическое занятие по учебной дисциплине: «Математика» Преподаватель Дмитрива В.М.
Тема: «ОСНОВНЫЕ ПРИЕМЫ РЕШЕНИЯ УРАВНЕНИЙ»
Цели занятия:
Обучающая: актуализация опорных знаний при решении уравнений; обобщение знаний об основных приемах решения уравнений; контроль знаний, умений и навыков; проверка усвоения темы на обязательном уровне.
Развивающая: Формирование умений рационально использовать приемы решения уравнений, развитие умения сравнивать, обобщать, правильно формулировать и излагать мысли, развитие умения быстро и правильно выбирать прием решения уравнений, проводить вычисления с привлечением простейших вычислительных средств.
Воспитательная: Воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.
Дидактическое оснащение практического занятия: комплект заданий для занятия, краткая инструкция для обучающихся.
План проведения:
изучить теорию;
разобрать предложенные примеры;
выполнить самостоятельно индивидуальные задания;
ответить на контрольные вопросы.
Время проведения 2 часа
Ход занятия
Орг. момент.
Проверка домашнего задания.
Изучение теории. (слайд 1-2)
- Основные приемы решения уравнений:
Разложение на множители;
Введение новых неизвестных;
Графический прием.
- Решим уравнения применяя основные приемы (решение уравнений у доски):
I. Разложение на множители (слайд 3)
- Уравнение вида 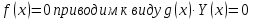 . Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю или оба одновременно.
. Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю или оба одновременно.
Пример 1 Решите уравнение 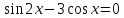 (
(
Решение.
ОДЗ: 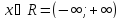
Применим формулу двойного аргумента: 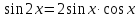 . Получим:
. Получим: 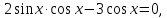
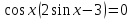 ,
,
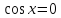 или
или 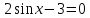
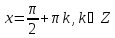
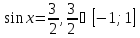 . решения нет.
. решения нет.
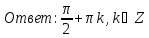
II. Введение новых неизвестных (или замены переменной) (слайд 4)
- Замену переменной в уравнении вводят так, чтобы привести уравнение к стандартному виду.
Пример 2. Решите уравнение методом замены переменной: х4 + 4х2 - 5 = 0.
Решение. Такие уравнения называются биквадратными. Перепишем его в виде: (х2)2 + 4х2 - 5 = 0. Замена: t = х2, тогда: t2 + 4 t – 5 = 0, t = -5 или t = 1.
Обратная замена: х2 = -5 или х2 = 1. Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня  1.
1.
Ответ:  1.
1.
III. Графический прием. (слайд 5)
- Для уравнения  на одном рисунке изобразим графики
на одном рисунке изобразим графики  . Точкам пересечения графиков этих функций соответствуют те значения аргумента х, при которых совпадают значения функции, то есть корни данного уравнения.
. Точкам пересечения графиков этих функций соответствуют те значения аргумента х, при которых совпадают значения функции, то есть корни данного уравнения.
Итак, абсциссы точек пересечения графиков  являются корнями уравнения
являются корнями уравнения 
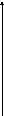
y


y=f(x)


y=g(x)
o
x
Пример 3 Решите графически уравнение: (х – 1 )2 = . (слайд 5)
Решение.
y
ОДЗ: х
Ответ:
4
1
o
1
1
x
Домашнее задание: на «3» 0.3 упр. № 10.5 (а,в) стр. 169; на «4-5» 0.3 упр. № 10.11 (б,г) стр. 270 (слайд 6)
Выполнение практической работы студентами. (слайд 7)
- Прочитайте инструкцию и выполните практическую работу № 80.
Краткая инструкция для обучающихся.
УВАЖАЕМЫЙ СТУДЕНТ!
Приступая к выполнению практической работы, Вы должны внимательно прочитать цель занятия, ознакомиться с краткими теоретическими и учебно-методическими материалами по теме практической работы, ответить на вопросы для закрепления теоретического материала и выполнить письменно задания в тетради для практических работ по дисциплине «Математика».
Правильное выполнение заданий оценивается баллами. Баллы, полученные за все выполненные задания, суммируются. Перед началом работы внимательно изучите критерии оценивания. Выполняйте задания в предложенном порядке. Пропускайте то задание, выполнение которого Вас затрудняет, и переходите к следующему. Если останется время, Вы сможете вернуться к пропущенным заданиям. В тетради для практических работ напишите номер практической работы, ее тему и цель.
Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов.
Наличие положительной отметки по практическим работам необходимо для получения отметки за семестр по дисциплине и допуска к экзамену, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной отметки за практическую работу Вы должны найти время для ее выполнения или пересдачи.
Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения консультаций и дополнительных занятий.
Время проведения дополнительных занятий и консультаций можно узнать у преподавателя или посмотреть на стенде в кабинете.
Желаем Вам успехов!!!
Практическая работа № 80.
Тема: Основные приемы решения уравнений.
Цель: Совершенствовать навыки решения уравнений
Порядок выполнения работы.
Рассмотрите теоретический материал и примеры решения задач.
Решите практическую работу и оформите решение письменно в тетради.
Краткие теоретические сведения к практической работе
Пример 1.
Решите уравнение методом разложения на множители: 2х2 + 3х = 0
Решение. Вынесем переменную х за скобки: х(2х + 3) = 0. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, х = 0 или 2х + 3 = 0. Значит, х = 0 или х = -1,5
Ответ: -1,5; 0.
Пример 2. Решите уравнение методом замены переменной: 4х - 3·2х +2 = 0
Решение. Переходим к одному основанию. 4х = (22)х = 22х
Получаем уравнение: 22х - 3·2х +2 = 0
Замена: 2х = t, тогда t2 - 3t+2 = 0
Решаем через дискриминант, получаем: t1 = 2, t2 = 1
Обратная замена: 1) t1 = 2, 2х = 2, х1 = 1
2) t2 = 1, 2х = 1, 2х = 20, х2 = 0
Ответ: 0; 1.
Пример 2. Решить графически уравнение: = 3 – x.
Строим по точкам графики двух функций у = и y = 3 – x и находим абсциссу точек пересечения графиков.
Ответ: 2
.Содержание практической работы
| Вариант 1 | Вариант 2 |
| 1. Решите уравнение: | |
| а) 5 | а) 3 |
| 2. Найдите корни уравнения: | |
| | |
| 3. Решите графически уравнение | |
|
| |
Контрольные вопросы:
Перечислить виды уравнений при решении своего варианта.
Сколько корней имеет простейшее показательное уравнение
при различных а и в?
При каких значениях а уравнение
не имеет решений?
Почему при решении уравнения вида f(x)=0 стараются разложить на множители левую часть?
Критерии оценки практической работы
| Задания | Баллы | Примечание |
| 1 | 4 | Каждое правильное задание 2 балла |
| 2 | 3 | Каждое правильное задание 3 балла |
| 3 | 4 | Каждое правильное задание 4 балла |
| Контрольные вопросы | 4 | Каждый правильный ответ 1 балл |
Максимальный балл за работу – 15 баллов
Шкала перевода баллов в отметки
| Отметка | Число баллов, необходимое для получения отметки |
| « 5» (отлично) | 14 – 15 |
| « 4» (хорошо) | 12 – 13 |
| « 3» (удовлетворительно) | 10 – 11 |
| « 2» (неудовлетворительно) | менее 10 |
Литература:
Для студентов
Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций: базовый и углубленный уровни /[С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]– М.: Просвещение, 2014. – 464 с. : ил. – (МГУ – школе).
Для преподавателей
Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций: базовый и углубленный уровни /[С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]– М.: Просвещение, 2014. – 464 с. : ил. – (МГУ – школе).
Интернет - ресурсы
www. fcior.edu.ru (Информационные, тренировочные и контрольные материалы).
www. school-collection.edu.ru (Единая коллекция цифровых образовательных ресурсов).
3

 Получите свидетельство
Получите свидетельство Вход
Вход












 Практическое занятие по учебной дисциплине: «Математика» (118.92 KB)
Практическое занятие по учебной дисциплине: «Математика» (118.92 KB)
 0
0 815
815 67
67 Нравится
0
Нравится
0



