ПРАКТИЧЕСКАЯ РАБОТА №1
ТЕМА: «Решение тригонометрических уравнений»
ЦЕЛЬ: «Обобщение, повторение и систематизация знаний по решению тригонометрических уравнений»
ЗАДАЧИ: 1.Отработать навыки решения уравнений на примерах.
2.Развивать логическое мышление, внимание, интерес к
предмету.
3.Воспитывать у учащихся чувство товарищества, ответственности,
настойчивости и упорства в достижении цели.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ.


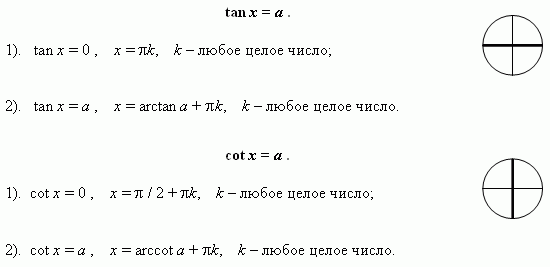
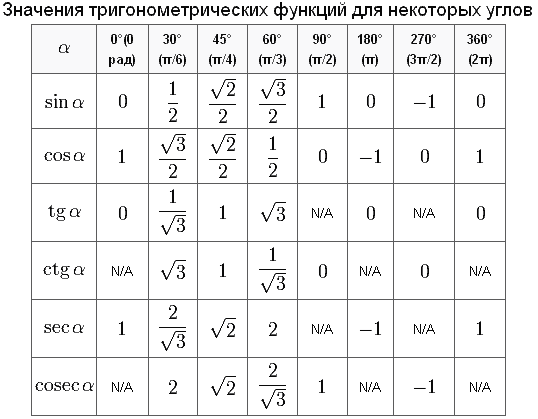
ЗАДАНИЯ:
1.Решите уравнение: sin x = -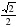
A) 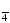 +
+ ;
; B) ±
B) ±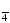 +2
+2 ;
; C) (-1)n+1
C) (-1)n+1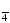 +
+ ;
;
D) (-1)n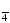 +
+ ;
; E)
E) 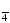 +2
+2 ;
;
2.Решите уравнение: cos x + 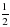 = 0
= 0
A) ±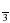 +2
+2 ;
; B)
B) 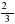 +
+ ;
; C)
C) 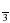 +2
+2 ;
; D) ±
D) ±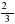 +2
+2 ;
;
E) ±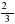 +
+ ;
;
3.Решите уравнение: 2cos x=0
A)  +2
+2 ;
; B)
B)  +
+ ;
; C)
C)  +
+ ;
; D)
D)  +2
+2 ;
;
E) 2 ;
;
4. Решите уравнение: 2 sin x = - 1
A) (-1)n+1 +
+ ;
; B) (-1)n+1
B) (-1)n+1 +
+ ;
; C) (-1)n
C) (-1)n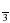 +
+ ;
;
D) (-1)n+1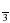 +
+ ;
; E) (-1)n
E) (-1)n +
+ ;
;
5.Решить уравнение: 2 cos x + 3 = 0
A)  arсcos
arсcos  +2
+2 ;
; B) Нет решений C) -arсcos
B) Нет решений C) -arсcos  +2
+2 ;
;
D) arсcos  +
+ ;
; E)
E)  arсcos 3+2
arсcos 3+2 ;
;
6.Решить уравнение: 2cos 6x -  = 0
= 0
A)  ;
; B) ±
B) ±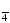 +2
+2 ;
; C)
C)  +
+ ;
; D)
D)  ;
;
E)  +2
+2 ;
;
7.Решить уравнение: 3 tg  =0
=0
A) - 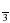 +2
+2 ;
; B) -
B) - +2
+2 ;
; C) -
C) - 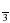 +
+ ;
; D) -
D) - +
+ ;
;
E)  +
+ ;
;
8.Решить систему уравнений: 
A) (3 n;
n; +
+
 ) n,
) n, 
 Z
Z B) (
B) ( n;
n; +
+
 ) n,
) n, 
 Z
Z C) (
C) ( n;
n; +2
+2
 ) n,
) n, 
 Z
Z E) (
E) ( n;
n; +3
+3
 ) n,
) n, 
 Z
Z  D) (
D) ( ;
;  +2
+2
 ) n,
) n, 
 Z
Z 9.Решить систему уравнений:
9.Решить систему уравнений: 
A) ( ;
; ) n,
) n,  Z B) (
Z B) ( ;
; ) n
) n Z
Z
C) ( ;
; ) n,
) n,  Z D) (
Z D) ( ;
; ) n,
) n,  Z
Z
E) ( ;
; ) n,
) n,  Z
Z
10.Решить уравнение: 2 sin2 x- sin x-1=0
A)  +2
+2 ;(-1)k+1
;(-1)k+1 +
+ ;k;
;k;  B)
B)  +2
+2 ;
;  C) (-1)n
C) (-1)n  +
+ ;
; 
D) (-1)n  +
+ ;
; +
+ ;
;  E)
E)  +2
+2 ;
; 
11.Решить уравнение: tg2 x+2tg x+1=0
A) 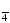 +
+ ;
; B)
B) 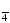 +2
+2 ;
; C) –
C) – 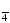 +2
+2 ;
; D) –
D) – 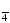 +
+ ;
;
12.Решить уравнение: 2 cos2 x – cos x=0
A)  +2
+2 ;
; B) ±
B) ±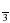 +
+ ;
; C)
C)  +
+ ;
;
D) 
 E)
E) 

13.Решите уравнение: sin 5x sin 4x + cos 6x cos 3x =0
A) 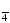 +
+ ;
; B)
B)  +2
+2 ;
; C)
C)  +
+ ;
;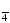 +
+ ;
; D)
D) 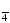 +
+ ;
; +2
+2 ;
; E)
E) 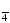 +
+ ;
; +
+ ;
;
14.Решите уравнение: sin2 x – 5sin xcos x + 4cos2 x = 0
A) 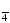 +
+ ;
; B)
B)  ,
, C) Нет решений D)
C) Нет решений D) 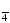 +
+ ;
; ;
; E)
E) 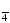 +2
+2 ;
; ;
;
15.Найдите решение уравнения sin2x +2sin 2x + 3cos2 x = 0
A)  ;
; B)
B)  ;
; ;
; C)
C)  ;
;
D)  ;
; ;
; E)
E)  ;
; ;
;
ПРАКТИЧЕСКАЯ РАБОТА №2
ТЕМА: « Решение тригонометрических неравенств»
ЦЕЛЬ: « Обобщить и систематизировать знания по решению
тригонометрических неравенств»
ЗАДАЧИ: 1.Отработать навыки решения неравенств для закрепления знаний
и умений.
2.Развивать познавательный интерес учащихся к предмету.
3.Воспитывать волю и настойчивость для достижения конечных
результатов.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ.
Неравенство  . Если
. Если  , то это неравенство решения не имеет, так как синус не может быть больше единицы. Если
, то это неравенство решения не имеет, так как синус не может быть больше единицы. Если  , то решением неравенства является любое число, так как синус всегда больше или равен -1. Рассмотрим теперь случай, когда а лежит на полуинтервале
, то решением неравенства является любое число, так как синус всегда больше или равен -1. Рассмотрим теперь случай, когда а лежит на полуинтервале  . Ответ:
. Ответ:  .
.
Неравенство  . Если
. Если  , то решением неравенства является любое число, так как синус всегда меньше или равен 1. Если
, то решением неравенства является любое число, так как синус всегда меньше или равен 1. Если  , то это неравенство решения не имеет, так как синус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале
, то это неравенство решения не имеет, так как синус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале  . Ответ:
. Ответ: 
Неравенство  . Если
. Если  , то это неравенство решения не имеет, так как косинус не может быть больше единицы. Если
, то это неравенство решения не имеет, так как косинус не может быть больше единицы. Если  , то решением неравенства является любое число, так как косинус всегда больше или равен -1. Рассмотрим теперь случай, когда а лежит на полуинтервале
, то решением неравенства является любое число, так как косинус всегда больше или равен -1. Рассмотрим теперь случай, когда а лежит на полуинтервале  . Ответ:
. Ответ: 
еравенство  . Если
. Если  , то решением неравенства является любое число, так как косинус всегда меньше или равен 1. Если
, то решением неравенства является любое число, так как косинус всегда меньше или равен 1. Если  , то это неравенство решения не имеет, так как косинус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале
, то это неравенство решения не имеет, так как косинус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале  . Ответ:
. Ответ: 
Неравенство  :
: 
Неравенство :
: 
Неравенство  :
: 
Неравенство  :
: 
Схема решений тригонометрических неравенств:
) n
РЕШИТЬ НЕРАВЕНСТВА САМОСТОЯТЕЛЬНО:
Найти значения х, при которых функция у = cos2x + 5cosx + 3 принимает неотрицательные значения.
Решение:
ЗАДАНИЯ:
1.Решить неравенство: 
A) [ ;
; ]
]  Z B) (
Z B) ( ;
; )
)  Z C) (
Z C) ( ;
; )
)  Z D) (
Z D) ( ;
; )
)  Z E) (
Z E) ( ;
; )
)  Z
Z
2. Решить неравенство: 
A) ( ;
; )
)  Z B) [
Z B) [ ;
; ]
]  Z
Z
C) [ ;
; ]
]  Z D) (
Z D) ( ;
; )
)  Z
Z
E) [ ;
; ]
]  Z
Z
3.Решить неравенство: 
A) ( ;
; )
)  Z B) (
Z B) ( ;
; )
)  Z C) [
Z C) [ ;
; ]
]  Z
Z
D) [ ;
; )
)  Z E) (
Z E) ( ;
; )
)  Z
Z
4.Решить неравенство:  A)
A)  ,
,  Z B)
Z B) ,
,  Z C)
Z C)  ,
,  Z
Z
D)  ,
,  Z E)
Z E)  ,
,  Z
Z
5. Решить неравенство: 
A)  ,
,  Z B)
Z B)  ,
,  C)
C)  ,
,  Z D)
Z D)  ,
,  Z
Z
E)  ,
,  Z
Z
6.Найти решение неравенства  на промежутке [
на промежутке [ ;
;  ]
]
A) [ ;
; ] B) [
] B) [ ;
; ] C) [
] C) [ ;
; ] D) [
] D) [ ;
; ] E) [
] E) [ ;
; ]
]
7,Решить неравенство: 
A)  ,
,  Z B)
Z B)  ,
,  Z
Z
C)  ,
,  Z D)
Z D)  ,
,  Z
Z
E)  ,
,  Z
Z
8.Решить неравенство: 
A)  ,
,  Z B)
Z B)  ,
,  Z
Z
C)  ,
,  Z D)
Z D)  ,
,  Z
Z
E)  ,
,  Z
Z
9.Решить неравенство : 
A)  B)
B) 
C)  D)
D) 
E) 
10.Решить неравенство : 
А) нет решений В)
С)  D)
D) 
E) 
11.Решить неравенство : 
A)  B)
B) 
C)  D)
D) 
E) 
12.Решить неравенство : 
A)  B)
B) 
C)  D)
D) 
E) 
13.Решить систему неравенств : 
 A)
A)  B)
B) 
C)  D)
D) 
Е) 
14.Решить систему неравенств : 
A)  B)
B) 
C)  D)
D) 
Е) 
15.Решить систему неравенств : 
A)  B)
B) 
C)  D)
D) 
Е) 
ПРАКТИЧЕСКАЯ РАБОТА №3
ТЕМА: « ПРОИЗВОДНАЯ . ПРАВИЛА ВЫЧИСЛЕНИЯ
ПРОИЗВОДНОЙ.ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ.»
ЦЕЛЬ: «Обобщение и систематизация знаний по теме производная»
ЗАДАЧИ: 1.Продолжить вырабатывать навыки нахождения производной
некоторых элементарных и сложных функций.
2.Развивать логическое мышление, интерес к предмету, глубже
Усвоить материал.
3.Воспитывать ответственность, организованность, настойчивость и
Упорство в достижении цели.
Правила дифференцирования:
Производная сложной функции:
Таблица производных
1)  ; 10)
; 10)  ;
;
2)  ; 11)
; 11)  ;
;
3)  ; 12)
; 12)  ;
;
4)  ; 13)
; 13)  ;
;
5)  ; 14)
; 14)  ;
;
6)  ; 15)
; 15)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
ЗАДАНИЯ:
1. Найдите производную функции g(х)=  х5+
х5+  х3−
х3−  х4
х4
A) 5х4 + 3х2−2х3 B) х4 + х2−2х3 C)  х4 +
х4 + х2−
х2− х3 D) х4 + х2−х3
х3 D) х4 + х2−х3
E)  х6+
х6+ х4−
х4−  х5
х5
2.Найдите производную функции u(х)=(х−5)(2х−5)
A) 4х−15 B) 4х2−15 C) 2х2−15х D) 4х+15 E) 2х2 −15
3.Найдите производную функции f (х)= 
A)  B)
B)  C)
C)  D)
D)  E)
E) 
3.Дана функция g(х)=2х4 −sinx+7.Найдите g′ (х)
A) 8х3- cosx B) 8х3+ cosx C) 4х2+ cosx +7 D) 8х3 −cosx +7 E) 8х2+ cosx
4.Дана функция у(х)=х+ .Найдите у′ (х)
.Найдите у′ (х)
A) 1+2 B) 1+
B) 1+ C)
C)  D) 1+
D) 1+ E) 1+
E) 1+
5.Найдите производную функции у(х)=3sinx+5cosx
A) 3cosx+5sinx B) −3cosx−5sinx C) 3cosx−5sinx D) −3cosx+5sinx
E) 3sinx−5cosx
6.Дана функция у(х)=2tgх − сtgх .Найдите у′ (х)
сtgх .Найдите у′ (х)
A)  B)
B)  C)
C)  D)
D) 
E) 
7.Дана функция у(х)=(5+ )(
)( −5)+
−5)+ Найдите у′ (х).
Найдите у′ (х).
A) 1+ B) 1−
B) 1− C) 5+
C) 5+ D) 5−
D) 5− E) 5+
E) 5+
8.Дана функция у(х)= cosx∙(sinx+1). Найдите у′ (х).
A) sin2x – sinx B) sin2x + sinx C) cos2x – sinx D) sinx-cos2x
E) cos2x + cosx
9.Дана функция у(х)= .Найдите у′ (х)
.Найдите у′ (х)
A)  B)
B)  C)
C)  D)
D) 
E) 
10.Дана функция f(х)= .Найдите f ′ (х).
.Найдите f ′ (х).
A)  B)
B)  C)
C)  D)
D)  E)
E) 
11.Дана функция f(х)=  х3− (2х−1)(2х+1).Найдите производную функции f (х) A)
х3− (2х−1)(2х+1).Найдите производную функции f (х) A)  х2 − 4х B)
х2 − 4х B)  х2 + 4х2 C) 3
х2 + 4х2 C) 3 х2 − 4х
х2 − 4х
D) 3 х2 − 8х E) 3
х2 − 8х E) 3 х2 + 8х2
х2 + 8х2
11.Найдите  если
если 
A)  B)
B)  C)
C)  D)
D) 
E)
12.Найдите  если
если 
A) B)
B)  C) 44(4х+7)10 D)
C) 44(4х+7)10 D)  E)
E) 
13.Найдите  , если
, если 
A)  B)
B)  C)
C)  D)
D) 
E) 
13.Найдите  , если
, если 
A) B)
B) 
C)  D)
D) 
E) 
14.Найдите производную 
A) B)
B)  C)
C) 
D) E)
E) 
15.Найдите  , если
, если 
A)  B)
B)  C)
C)  D)
D)  E)
E) 
16.Найдите  , если
, если 
A) B)
B)  C)
C)  D)
D)  E)
E) 
17.Найдите производную функции f(х)= ех−5х3
A) ех−15х2 B) ех−3х5 C) 1−15х2 D) ех − х3 E) 1−15х4
18.Дана функция h(х)= 3ех+ cosx+ р. Найдите h′ (х).
A) 3ех − sinx+ р B) 3ех – sinx C) 3ех+ sinx + р D) 3ех+ sinx E) 3ех+cosx
19.Дана функция  Найдите производную
Найдите производную 
A)  B)
B)  C)
C)  D)
D)  E)
E) 
20.Найдите  , если
, если 
A)  B)
B)  C)
C)  D)
D)  E)
E) 
ПРАКТИЧЕСКАЯ РАБОТА №4
ТЕМА: « ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ НА ОТРЕЗКЕ.»
ЦЕЛЬ: « Обобщение, повторение и систематизация знаний по теме
производная и ее применение»
ЗАДАЧИ:1.Применение производной к решению конкретных задач на
составление уравнения касательной ,движения материальной
точки, нахождения наибольшего и наименьшего значения функции»
2.Развивать познавательный интерес учащихся к предмету.
3.Воспитывать волю и настойчивость для достижения конечных
результатов.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ:
ЗАДАНИЯ:
1.Напишите уравнение касательной к графику функции у= х2 −2х в точке х0=3
A) у= 4х – 9 B) у – 9х+4=0 C) у= −4х + 9 D) у= −9х + 4 E) у – 4х +3=0
2.Угловой коэффициент касательной, к графику функции у= sin2x в точке х0= равен :
равен :
A) k = B) k = 2 C) k =−1 D) k = 0 E) k = 1
B) k = 2 C) k =−1 D) k = 0 E) k = 1
3.Найдите угловой коэффициент касательной к графику функции у(х) = 3cos2x в точке х0=
3cos2x в точке х0= 
A) −3 B)  C)
C)  D)
D)  E)
E) 
4.Напишите уравнение касательной к графику функции у= 2 –2 х2 в точке
х0= 2
A) у = − 8х + 10 B) у – 8х+10=0 C) у=10+6х D) у + 6х+10=0 E) у = 10х – 8
5.Напишите уравнение касательной к графику функции у =  в точке х0= 1
в точке х0= 1
A) у = х−1 B) у + х = 0 C) у = 2х D) у + 2х = 0 E) у = 1−2х
6.Тело движется по прямой так, что расстояние от начальной точки изменяется по закону S=  х4 +3х3 – х2 (м). Найдите ускорение тела через 0,5с после начала движения.
х4 +3х3 – х2 (м). Найдите ускорение тела через 0,5с после начала движения.
A) 7,25 м/с² B) 6,75 м/с² C) 7,75 м/с² D) 5,67 м/с² E) 6,57 м/с²
7.Найдите наименьшее значение функции у (х)= 3х3 – 9 на отрезке [0;3]
A) – 9 B) − 6 C) – 90 D) – 27 E) – 12
8.Для заданного закона движения точки  вычислите, в какой момент времени скорость равна 5.
вычислите, в какой момент времени скорость равна 5.
А)1 В)2 С)4 Д)3 Е)1,2
9.Найдите наибольшее и наименьшее значения функции у(х)= х+  на отрезке [0,5;2]
на отрезке [0,5;2]
A) ; 2 B)
; 2 B) ; 2 C)
; 2 C)  ; −2 D)
; −2 D)  ; −2 E) 2; −2
; −2 E) 2; −2
10.Найдите наибольшее и наименьшее значения функции у (х)= 7х3− 3,5х2+2 на отрезке [ 1;2]
A) 5,5; 4,4 B) 5,05; 4,04 C) −55; − 44 D) 55; − 4,4 E) 44; 5,5
11.Найдите наибольшее и наименьшее значения функции f(х)=  х5 – 4х2 + 6 на отрезке [0; 2] A) 6,3; 3,6 B) 6; −3,6 C) 6; 3,6 D) 6,3; 6 E) 3,6; 3
х5 – 4х2 + 6 на отрезке [0; 2] A) 6,3; 3,6 B) 6; −3,6 C) 6; 3,6 D) 6,3; 6 E) 3,6; 3
12.Найдите угловой коэффициент касательной, проведенной к параболе
у= х2 −5х+ 6 в точке х0= 2
A) k =1 B) k = −1 C) k =0 D) k =12 E) k =5
13.К графику функции у =  проведена касательная в точке х0= 4. Найдите абсциссу точки касательной, если её ордината равна
проведена касательная в точке х0= 4. Найдите абсциссу точки касательной, если её ордината равна 
A) 12 B) 4 C)  D) – 12 E) – 4
D) – 12 E) – 4
14.Из предложенных ответов выбери наибольшее и наименьшее значения для функции у =  (2х +1)3 на отрезке [
(2х +1)3 на отрезке [ ; 1]
; 1]
A) 9; 0 B) 9; 1 C) 8;−9 D) 1;−8 E) 9;−1
15.Найдите критические точки экстремума функции f(х)=х4 − 8х2+6 .
A) хmin= 0; хmax= 2. B) хmax= 0; хmin= −2. C) хmin= ±2; хmax= 0.
D) хmin= −2; хmax= 2. E) хmax= ±2 ; хmin= 0.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Понятие тригонометрических функций, уравнений, неравенств - одно из фундаментальных понятий школьного курса математики .
Умение решать уравнения и неравенства различных видов позволяет обеспечить базовую подготовку школьника для успешного прохождения итоговой аттестации по математике за курс средней школы. Не менее важным является и изучение Производной. Поэтому и появилась необходимость в конце учебного года создание практических работ , которые охватывают повторение всего курса математики за 10 класс. Практические работы состоят из тестовых заданий, которые учащиеся должны обязательно решить и записать ответ. Это вызвано тем, что за курс средней школы учащиеся будут сдавать ЕНТ. В этот блок не вошла еще одна практическая работа на тему : « исследование функции и построение графиков функций», но эта работа отличается от данных, тем что там нет тестовых заданий. Некоторые задания выходят за рамки программного материала, но они не сложны и учащиеся могут их свободно выполнить, пользуясь справочным материалом.
БУЛАЕВСКАЯ СРЕДНЯЯ ШКОЛА №2
Практические работы по математике за курс 10 класса.
Подготовила учитель математики
1 категории
Гапонова И.Б.
2012


 Получите свидетельство
Получите свидетельство Вход
Вход




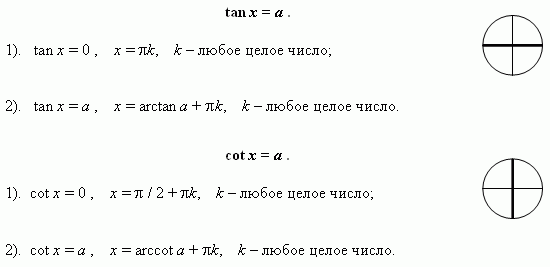

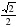
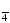 +
+ ;
; B) ±
B) ±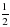 = 0
= 0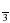 +2
+2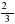 +
+








 Практические работы по алгебре (10 класс) (1.01 MB)
Практические работы по алгебре (10 класс) (1.01 MB)
 0
0 13033
13033 2077
2077 Нравится
0
Нравится
0



