Ппрактикум по математике "Задачи по теории вероятностей"

Большую роль при изучении тем по теории вероятностей и статистики играют задачи. Отношения учащихся к процессу решения задач зависит от многих параметров: от условия задачи (абстрактная или связанная с жизненной ситуацией), от методов и способов решения этих задач и, др.

Практика показывает, что у учащихся появляется интерес, и они более активно включаются в процесс решения задач, если задачи по данным темам связаны с жизненными ситуациями.

Для более глубокого понимания теоретического материала, для развития мышления, необходимо:

 - вовлекать учащихся в процесс решения этих задач;

 - рассматривать несколько способов решения данных задач;

 - рассматривать все события и делать проверку и др.

При организации процесса решения задач мы следуем принципу: «Лучше решить задач меньше, но более обстоятельно, чем много, но поверхностно»

Задачный материал по каждой теме должен быть подобран таким образом, чтобы его решение способствовало уяснению учащимися данной темы и новых математических идей, заложенных в ней; помогало осуществить повторение предыдущего материала на основе нового, решить старые задачи новыми методами; содержало бы в себе пропедевтику последующих тем курса.

При обучении решению задач следует реализовать принцип тесной взаимосвязи различных тем математики.

Роль внутрипредметных связей в учебном процессе велика; они непосредственно влияют на достижение обучающей, развивающей и воспитывающей целей обучения. При этом внутрипредметные связи формируют у учащихся научное мировоззрение, помогают видеть мир в движении и развитии, способствуют установлению логических связей между понятиями, тем самым развивают логическое мышление учащихся. Внутрипредметные связи выступают средством предупреждения и ликвидации формализма в знаниях школьников, позволяют сформировать такую систему знаний, которая предстает перед учащимися не как застывшая, а как динамичная, качественно изменяющаяся. Сокращают затраты учебного времени, способствуют устранению перегрузки школьников.

Возможность осуществления этого принципа мы рассмотрим на примере решения поисковых задач по теме «Теория вероятностей» Рассмотрим несколько задач:

Задача 1

В партии из 10 деталей находится 4 бракованных. Наугад выбирают три детали. Найти вероятность того, что из этих трех деталей две детали окажутся бракованными.

Решение.

Число всех равновозможных независимых исходов п равно числу сочетаний из 10 по 3, т.е. 

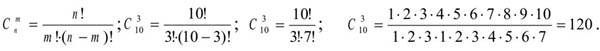
Подсчитаем число исходов т, благоприятствующих событию А. Среди 3 взятых наугад деталей должна быть одна качественная и две бракованных.

Весь материал - смотрите документ.