Позиционные системы счисления

Позиционные системы счисления

Основные понятия

• Система счисления – способ записи чисел

• В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа.

• Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.

• Основанием позиционной системы счисления называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию .

В позиционной системе счисления любое число в развернутой форме может быть представлено в следующем виде:

А q = ± (a n-1 q n-1 +a n-2 q n-2 +...+a 0 q 0 +a -1 q -1 +a -2 q -2 +...+a -m q -m )

Здесь

А — само число,

q — основание системы счисления,

a i —цифры, принадлежащие алфавиту данной системы счисления,

n — число целых разрядов числа,

m — число дробных разрядов числа.

Десятичное число А 10 =4718 в развернутой форме запишется так:

А 10 =4·10 3 +7·10 2 +1·10 1 +8·10 0

Двоичное число А 2 =1001 в развернутом виде:

А 2 =1·2 3 +0·2 2 +0·2 1 +1·2 0 =8+0+0+1=9

Восьмеричное число А 8 =7764 в развернутом виде:

А 8 =7·8 3 +7·8 2 +6·8 1 +4·8 0 =3584+448+48+4=

=4080

Шестнадцатеричное число 3АF 16 в развернутом виде:

3АF 16 = 3·16 2 +10·16 1 +15·16 0 =768+160+15=943

Чтобы перевести число в десятичную систему счисления, нужно:

• Записать число в развернутой форме;
• Вычислить значение полученного выражения.

Пример:

45,25 8 =4*8 1 +5*8 0 +2*8 -1 +5*8 -2 =32+5+2/8+5/64=37,328125

101011,11 2 =1*2 5 +0*2 4 +1*2 3 +0*2 2 +1*2 1 +1*2 0 +1*2 -1 +1*2 -2 =32+8+2+1+

+1/2+1/4=43,75

12,4 16 =1*16 1 +2*16 0 +4*16 -1 =16+2+4/16=18,25

Задания для самостоятельного выполнения:

Запишите числа

1111101 2 , 123 8 , F3 16, 1101011,01 2, 23,5 8 F,3 16

в десятичной системе счисления.

Перевод целых чисел из десятичной системы счисления в систему счисления с произвольным основанием

Перевести десятичное число 173 10 в восьмеричную систему счисления:

Получаем: 173 10 =255 8

• Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
• Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
• Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Перевод целых чисел

Перевести десятичное число 173 10 в двоичную систему счисления:

Получаем: 173 10 =10101101 2

• Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
• Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
• Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Перевод целых чисел

Перевести десятичное число 173 10 в шестнадцатеричную систему счисления:

Получаем: 173 10 =AD 16

• Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
• Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
• Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Задания для самостоятельного выполнения:

Переведите числа

456, 48, 321

в двоичную, восьмеричную и

шестнадцатеричную системы счисления.

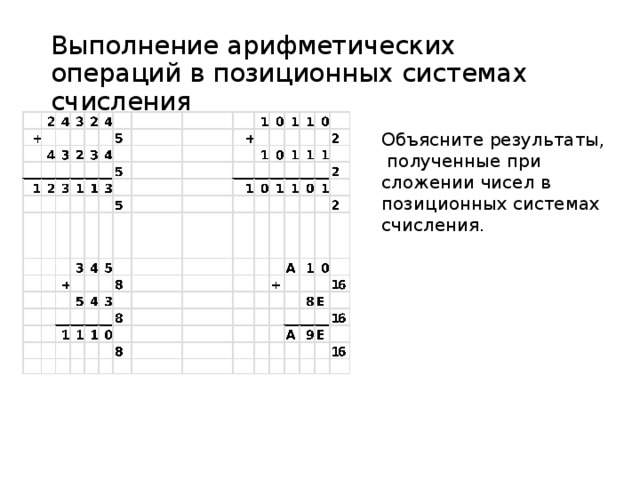
Выполнение арифметических операций в позиционных системах счисления

Объясните результаты, полученные при сложении чисел в позиционных системах счисления.

Перевод дробных чисел из одной системы  счисления  в другую

• 1. Основание новой системы счисления  выразить  цифрами  исходной системы счисления  и  все последующие действия производить в исходной системе счисления.
• 2. Последовательно  умножать  данное  число  и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения  не станет равной нулю или будет достигнута требуемая точность представления числа.
• 3. Полученные целые части произведений,  являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом  новой системы счисления.
• 4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Перевод дробных чисел из одной системы  счисления  в другую

Перевод произвольных чисел

• Перевод произвольных чисел,  т.е. чисел, содержащих целую и дробную части,  осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2 n  и обратно

  Перевод целых чисел.  Для того, чтобы целое двоичное число записать в системе счисления с основанием q=2 n , нужно:

• 1. Двоичное число разбить справа налево на группы по n  цифр в каждой.
• 2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.
• 3. Рассмотреть каждую группу как n-разрядное двоичное число и  записать ее соответствующей цифрой в системе счисления с основанием q=2 n .

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2 n  и обратно

  Перевод дробных чисел.  Для  того,  чтобы  дробное двоичное число записать в системе счисления с основанием q=2 n , нужно:

1. Двоичное число разбить слева направо на группы по n  цифр в каждой.

2. Если  в последней правой группе окажется меньше n разрядов,  то ее надо дополнить справа нулями до нужного числа разрядов.

3. Рассмотреть каждую группу как n-разрядное двоичное число и  записать ее соответствующей цифрой в системе счисления с основанием q=2 n .

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2 n  и обратно

  Перевод произвольных чисел.  Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2 n , нужно:

1. Целую часть данного  двоичного  числа  разбить  справа налево, а дробную — слева направо на группы по n цифр в каждой.

2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями  до нужного числа разрядов;

3.  Рассмотреть  каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2 n

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2 n  и обратно

  Перевод чисел из систем счисления с основанием q=2 n  в двоичную систему.  Для того, чтобы произвольное число, записанное в системе счисления с основанием q=2 n , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-значным эквивалентом в двоичной системе счисления.

Задания для самостоятельного выполнения