Построение проекций многогранников

Предмет «Черчение» 9 класс

Урок № 20

Тема: Построение проекций многогранников

Цели урока: дать уч-ся понятие о многогранниках;

образовательные: Дать понятие о методе проекций, о видах проецирования; воспитательные: воспитывать точность и аккуратность, внимательность и усидчивость;

развивающие: развивать пространственное представление и пространственное мышление;

урок изучения нового материала;

Тип урока: урок изучения нового материала; Методы обучения: словесный , наглядный, практический ,гностический, управленческий;

Меж предметные связи: геометрия, технология; начертательная геометрия;

Дидактическое обеспечение:

таблицы , плакаты; модель фронтальной и горизонталь­ной плоскостей проекций и предмета, карточки - задания;

Тип практической работы: выполнение упражнении в тетради; конспектирование в тетради;

Ход урока:

1. Организационный момент: — приветствие;

— организация внимания учащихся;

— раскрытие целей урока.

2. Актуализация.

Учащиеся, исходя из темы урока, должны сформулировать задачи на урок.

Спланировать работу по заданной теме.

3. Формирование новых знаний.

Актуализация: уметь самостоятельно выполнить аналогичное задание;

Формирование новых понятий и способов действий:

Какой материал отрабатывается: практические умения и навыки при построении сопряжений;

Планирование формирования обратной связи: создание рабочей обстановки; поощрять работу детей, строить объяснение материала в форме вопросов и ответов;

Построение проекций многогранников

Построение проекции многогранника на некоторой плоскости сводится к построению проекций точек. Например, проецируя пирамиду SABC на пл.я₂ (рис. 256, слева), мы строим проекции вершин S, А, В и С и, как следствие, проекции основания ABC, граней SAB, SBC, SAC, ребер SA, SB и др. Также, проецируя трехгранный угол ') с вершиной S (рис. 256, справа), мы, помимо вершины S, берем на ребрах угла по одной точке (К, М, N) и проецируем их на пл. я₂; в результате получаем проекции ребер и граней (плоских углов) трехгранного угла и В целом самый угол. На рис. 257 изображены многогранное тело ACBB₁D... (т. е. часть пространства, ограниченного со всех сторон плоскими фигурами — многоугольниками) и его проекция на пл. я₁ — фигура A'C'F [E[DID'E'F'. Каждая точка, расположенная внутри очерка этой фигуры (т. е. линии, ограничивающей ее), является проекцией по крайней мере двух точек поверхности этого тела. Например, точка с двойным обозначением М' и N' служит проекцией точек М и N, лежащих на общей для них проецирующей прямой.

Точка, лежащая на самом очерке проекции, является проекцией или одной точки (например, А' есть проекция точки А), или нескольких, а иногда и множества точек (например, В' является проекцией не только точки В, но и множества точек грани ABC, расположенных на проецирующей прямой В В').

Проецирующие прямые, проходящие через все точки очерка проекции, в своей совокупности образуют проецирующую поверхность, внутри которой, касаясь ее, заключено данное тело. Для тела, изображенного на рис. 257, проецирующая поверхность состоит из плоскостей о^, а₂, а₃ и т. д. Линия касания проецирующей поверх') В данном случае выпуклый, т. е. такой, который весь расположен по одну сторону от плоскости каждой из его граней, неограниченно продолженной.

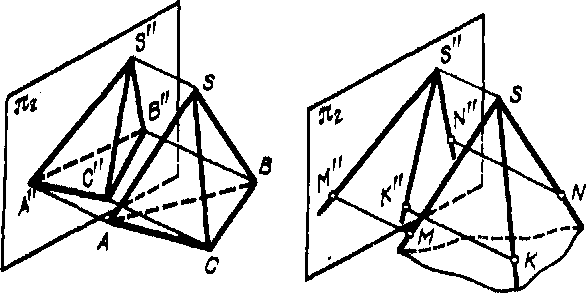
Рис. 256

ности и тела называется контуром тела по отношению к выбранной плоскости проекций. На рис. 257 таким контуром служит ломаная ACF₁E₁D₁DEFA ¹).

Проецирующей поверхностью при параллельном проецировании является, как это указывалось в § 1, поверхность цилиндрическая. Если контур тела по отношению к плоскости проекций содержит прямолинейные отрезки, то проецирующая поверхность для каждого такого участка обращается в плоскую.

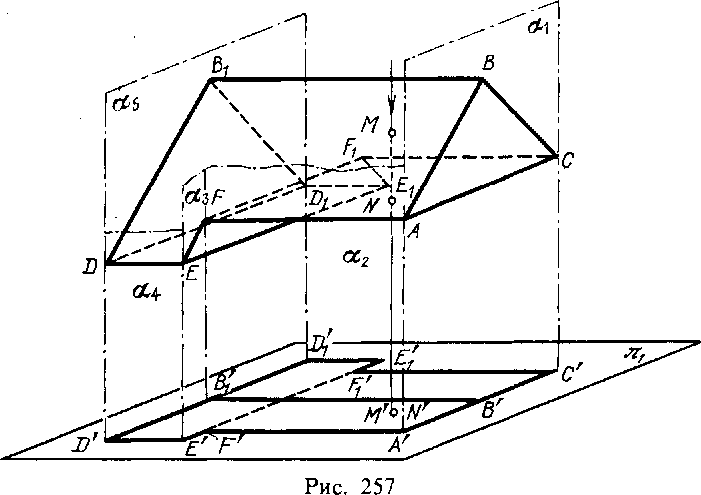
Проведенная на проекции прямая В'В{ является проекцией ребра BB_V видимого по отношению к пл. п₁. Показ на проекции тела всех видимых его ребер является обязательным.

Проекция отрезка FF₁ получается внутри очерка проекции; она показана штриховой линией, так как, по условиям видимости, точки отрезка FF_i при проецировании на пл. невидимы.

Построение проекции гранной поверхности также сводится к построению проекций некоторых точек и прямых линий этой поверхности. Проекция поверхности, ограничивающей какое-либо тело, имеет очерк, общий с очерком проекции этого тела. В случае изображения бесконечно простирающейся поверхности отделяют линиями некоторую ее часть и тем устанавливают условный контур по отношению к плоскости проекций.

Понятие многогранника. Виды многогранников

Многогранником называется тело, поверхность которого состоит из конечного числа плоских многоугольников. Среди многогранников выделим призмы, пирамиды, призматоиды и правильные многогранники.

Призмой называется многогранник, который состоит из двух плоских многоугольников ñ оснований, совмещаемых при параллельном переносе, и боковой поверхности, состоящей из параллелограммов, две стороны которых являются соответствующими сторонами оснований, а две другие ñ соседними боковыми ребрами призмы. Высотой призмы называется расстояние между плоскостями ее оснований.

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. Прямая призма называется правильной, если ее основаниями являются правильные многоугольники.

Пирамидой называется многогранник, который состоит из плоского многогранника ñ основания пирамиды, точки, не лежащей в плоскости основания, ñ вершины пирамиды и всех отрезков, соединяющих вершину с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются ребрами. Боковые грани пирамиды ñ треугольники. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамида называется n-угольной, если ее основанием является n-угольник.

Треугольная пирамида называется также тетраэдром. Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника. У правильной пирамиды боковые ребра равны; следовательно, боковые грани ñ равные равнобедренные треугольники. Среди пирамид выделяют усеченные пирамиды. Они получаются при пересечении пирамиды плоскостью, параллельной основанию. Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями усеченной пирамиды, остальные грани называются боковыми гранями. Основания усеченной пирамиды представляют собой подобные многоугольники, боковые грани ñ трапеции.

.

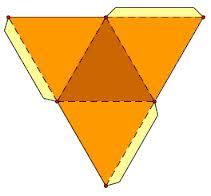
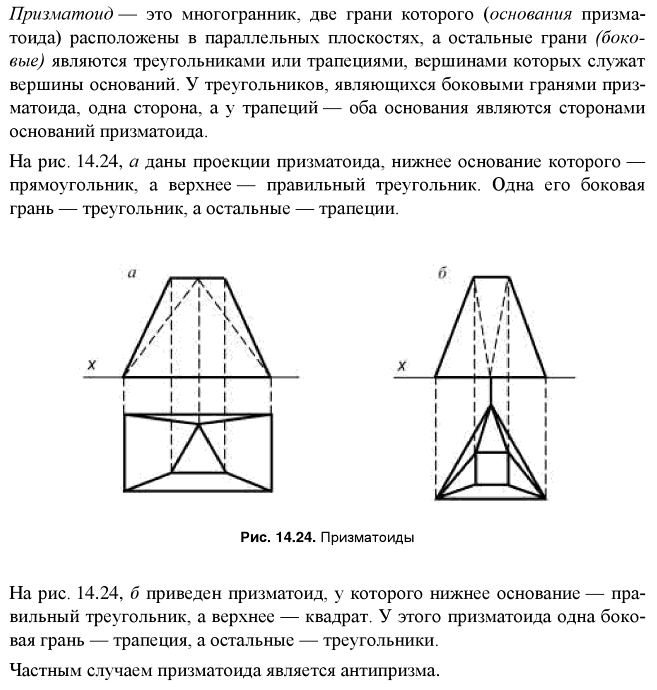В таком многограннике параллельные основания представляют собой многоугольники с произвольным числом сторон, а грани ñ треугольники или трапеции. Многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

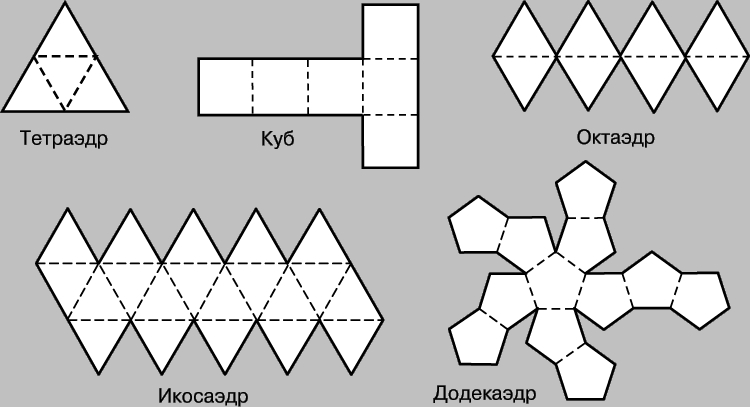
Существует пять типов правильных многогранников.

Правильный тетраэдр ñ грани являются правильными треугольниками, в каждой его вершине сходятся три ребра. Куб ñ грани являются квадратами, вкаждой его вершине сходятся три ребра.

Октаэдр ñ грани являются правильными многоугольниками, в каждой еговершине сходятся четыре ребра.

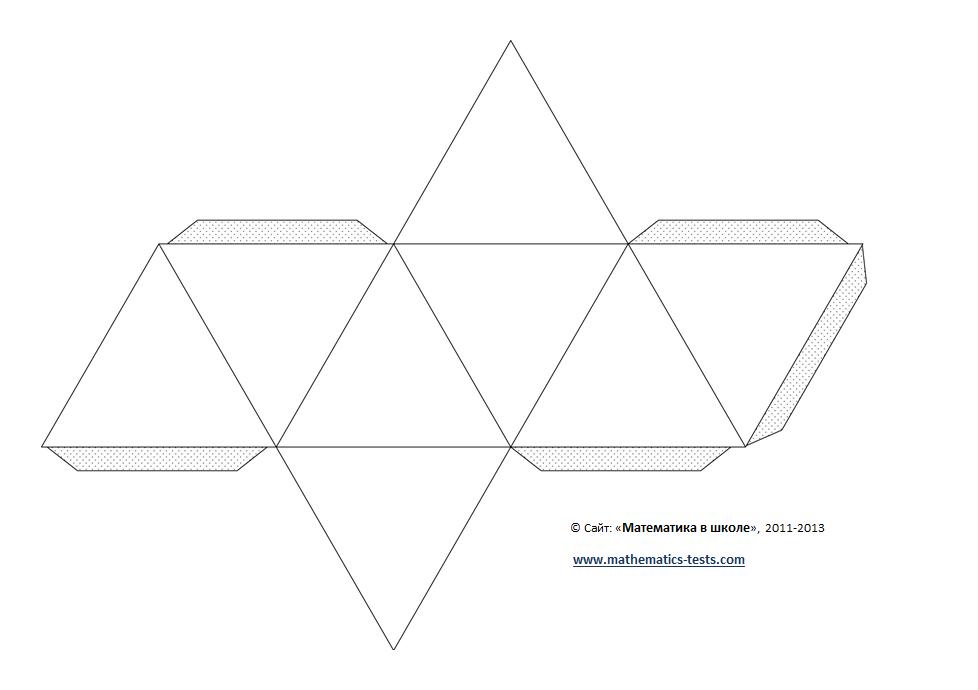
Додекаэдр ñ грани являются правильными пятиугольниками, в каждой его вершине сходятся три ребра.

Делаем правильный додекаэдр

Самый первый этап в изготовлении – построение пятиугольника нужного размера. Должен получиться вот такой элемент. Он и станет основой фигуры.

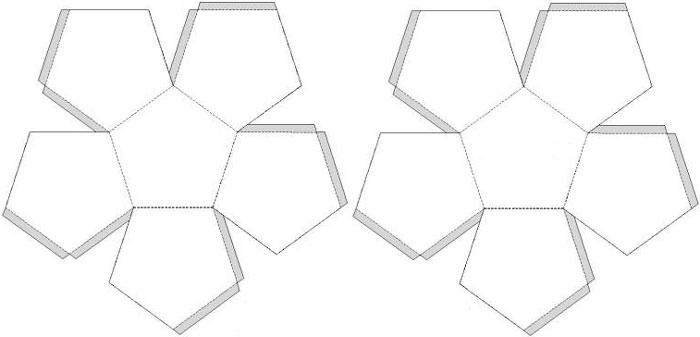
Далее конструируете развертку додекаэдра с учетом припусков на склеивание. В результате получится «выкройка» приблизительно такого вида. Варианты могут различаться, если припуски будут другой формы или размещены на других гранях.

Аккуратно по линиям сгибаете припуски. Склеиваете. Наносите на готовый додекаэдр нужный рисунок или декорируете другим выбранным способом.

Исокаэдр ñ гранями являются правильные треугольники, в каждой вершине сходятся пять ребер.