Построение на плоскости в Geogebra

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«Мордовский государственный педагогический институт

имени М.Е. евсевьева»

  ПОСТРОЕНИЕ НА ПЛОСКОСТИ В GEOGEBRA Реферат

Выполнила: студентка 5 курса МДИ-112

Христофорова А.В.

Проверила: канд. физ.-мат. н., доцент Кормилицына Т.В.

Динамическая геометрия

• Динамическая геометрия – это программная среда, с помощью которой можно делать геометрические построения на компьютере так, что при движении первоначальных объектов, весь чертёж сохраняется.

Наиболее известные системы динамической геометрии:

• Cinderella (автор Ulrich Kortenkamp);
• Математический Конструктор (разработано 1С);
• GEONExT (автор Alfred Wassermann);
• «The Geometer's Sketchpad» (русифицирована Институтом Новых Технологий и распространялась в России вначале под названием «Живая геометрия», а затем «Живая математика»);
• программная среда Compass and Ruler (C.a.R) (автор Rene Grothmann), GeoGebra (автор Marcus Hohenwater, 2002 год).

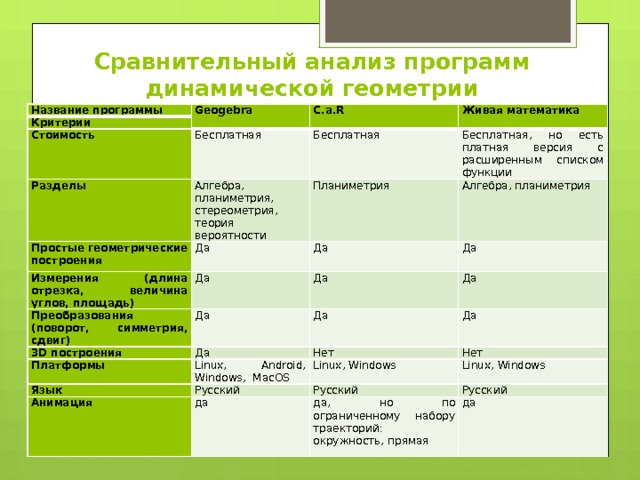
Сравнительный анализ программ динамической геометрии

Название программы

Geogebra

Критерии

Стоимость

C.a.R

Бесплатная

Разделы

Живая математика

Алгебра, планиметрия, стереометрия, теория вероятности

Бесплатная

Простые геометрические построения

Планиметрия

Да

Бесплатная, но есть платная версия с расширенным списком функции

Измерения (длина отрезка, величина углов, площадь)

Да

Алгебра, планиметрия

Да

Преобразования (поворот, симметрия, сдвиг)

Да

3D построения

Да

Да

Да

Да

Платформы

Да

Linux, Android, Windows, MacOS

Язык

Нет

Да

Русский

Нет

Анимация

Linux, Windows

да

Русский

Linux, Windows

Русский

да, но по ограниченному набору траекторий: окружность, прямая

да

Проведя сравнительный анализ данных программ, можем увидеть, что программа GeoGebra обладает большими достоинствами и возможностями, по сравнению с другими средами динамической геометрии:

• GeoGebra является бесплатной программной, может свободно копироваться и использоваться как в образовательном учреждении, так и на домашнем компьютере;

• Может ставиться на различные операционные системы, такие как Windows, MacOS, Linux и Android;

• Интерфейс программы реализован на 40 языках, в том числе и на русском;

• На сайте официальном сайте программной среды постоянно появляются обновленные версии;

• GeoGebra позволяет работать с матрицами, с комплексными числами, с таблицами, со статистическими функциями, в программе реализована возможность аппроксимировать множество точек кривой заданного вида.

Динамическая геометрическая среда Geogebra

• GeoGebra – это программная среда, которая благодаря своей динамической структуре, объединила в себе важные представления математических понятий: табличное, алгебраическое и геометрическое представления.

• GeoGebra позволяет создавать различные конструкции из точек, отрезков, векторов, прямых, окружностей, математических функций и других базовых элементов, а затем динамически изменять их и строить анимации. Благодаря тому, что в программе реализована возможность напрямую вводить уравнения и работать с координатами, можно наглядно строить графики функций, работать с ползунками для подбора параметров.

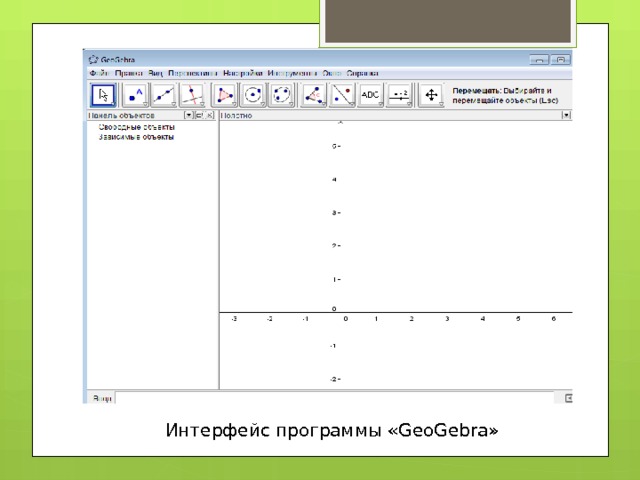
Интерфейс программы «GeoGebra»

• Программа написана Маркусом Хохенвартером на языке Java (работает на большом числе операционных систем), переведена на 39 языков и полностью поддерживает русский язык.

Официальный сайт Geogebra

Систему можно использовать для построения линий:

• построение графиков функций y = f (x);
• построение кривых, заданных параметрически в декартовой системе координат: x = f(t); y = g(t)
• построение конических сечений:
• коника произвольного вида — по пяти точкам.
• окружность по центру и точке на ней, по центру и радиусу, по трем точкам;
• эллипс – по двум фокусам и точке на кривой;
• парабола – по фокусу и директрисе;
• гипербола – по двум фокусам и точке на кривой;
• В системе предусмотрена возможность построения геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику (инструмент локус).

Кроме графических действий в системе могут быть выполнены вычисления:

• действия с матрицами: сложение, умножение; транспонирование, инвертирование; вычисление определителя;
• вычисления с комплексными числами;
• нахождение точек пересечения кривых;

статистические функции:

• вычисление математического ожидания, дисперсии;
• вычисление коэффициента корреляции;
• аппроксимация множества точек кривой заданного вида: полином; экспонента; логарифм; синусоида.

Примеры геометрических построений на плоскости с помощью программы Geogebra

Пример 1.

Найдите геометрическое место центров окружностей, проходящих через две данные точки.

Решение.

Пусть окружность с центром О проходит через данные точки А и В . Поскольку ОА = ОВ (как радиусы одной окружности), точка О лежит на серединном перпендикуляре к отрезку АВ . Обратно, каждая точка О , лежащая на серединном перпендикуляре к АВ , равноудалена от точек А и В .

Шаги создания чертежа в GeoGebra:

1. С помощью инструмента «отрезок по двум точкам» (на панели инструментов), строим отрезок АВ произвольной длины.

2. Строим окружность с с центром в точке О , проходящую через концы отрезка АВ (с помощью инструмента «окружность по центру и точке»).

3. Строим окружность d с центром О1 , проходящую через концы отрезка АВ и пересекающую окружность с (инструмент «окружность по центру и двум точкам»).

4. С помощью инструмента «отрезок по двум точкам» соединяем попарно точки О и О1 , точки О и А , точки А и О1 , точки О1 и В , точки В и О .

Из чертежа видно, что ОА = ОВ – как радиусы окружности с , О1А = О1В – радиусы окружности d . Точка О лежит на серединном перпендикуляре к АВ , так как равноудалена от концов этого отрезка (для О1 – аналогично).

Графическое решение примера 1

Пример 2.

Даны окружность S и точка M вне ее. Через точку M проводятся все возможные окружности S1 , пересекающие окружность S . Х – точка пересечения касательной в точке M к окружности S1 с продолжением общей хорды окружностей S и S1 . Найдите геометрическое место точки Х .

Решение .

Пусть А и В – точки пересечения окружностей S и S1 . Тогда XM XM = XA , XB = XO XO - R R , где O и R соответственно центр и радиус окружности S . Поэтому XO XO - XM XM = R R , а значит, точка X лежит на перпендикуляре к прямой OM .

Шаги создания чертежа в GeoGebra:

1. С помощью инструмента «окружность по центру и точке на ней» строим окружность S с центром O .

2. Окружность S1 с центром O1 , строим аналогично и таким образом, чтобы она пересекала окружность S .

3. Отметим точку А и точку В на пересечении окружностей (инструмент «пересечение» или «точка»).

4. Проведем касательную к окружности S1 (инструмент «касательная»), отметим точку касания М (инструмент «точка»).

5. С помощью инструмента «луч по двум точкам» проведем общую хорду.

6. Отметим точку пересечения хорды и касательной, точка Х (инструмент «пересечение» или «точка»).

7. Выделим треугольники АХМ и ОХВ (инструмент «многоугольник»).

8. Проведем прямую ОМ (инструмент «луч по двум точкам»).

9. Опустим перпендикуляр из точки Х на OM (инструмент «перпендикулярная прямая»).

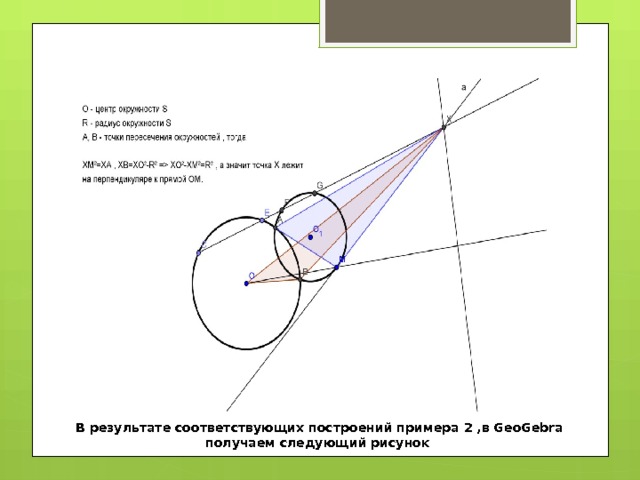
В результате соответствующих построений примера 2 ,в GeoGebra получаем следующий рисунок

Система GeoGebra как универсальный программный продукт, сочетающий в себе свойства систем динамической геометрии, систем вычислительной математики, является полноценной компьютерной математической средой, и это дает основания для использования ее в обучении геометрии.