Дидактические материалы
« Математика 2 курс»
Предисловие
«Дидактические материалы» предназначены для организации самостоятельной работы учащихся и контроля за знаниями и умениями при обучении в «Арзамасском приборостроительном колледже им П.И.Пландина».
Содержащиеся в сборнике работы делятся на два вид: самостоятельные работы и контрольные работы.
Самостоятельные работы даны в четырех вариантах. По своему целевому назначению они могут использоваться как обучающие, так и для контроля знаний и умений по теме.
С а м о с т о я т е л ь н ы е р а б о т ы.
Вариант 1.
С-1. Дифференциальное и интегральное исчисление.
Вычисление пределов функции.
1). ![]() 2).
2). ![]() 3).
3). ![]() 4).
4). ![]() 5).
5). ![]() .
.
2. Исследовать функцию на непрерывность.
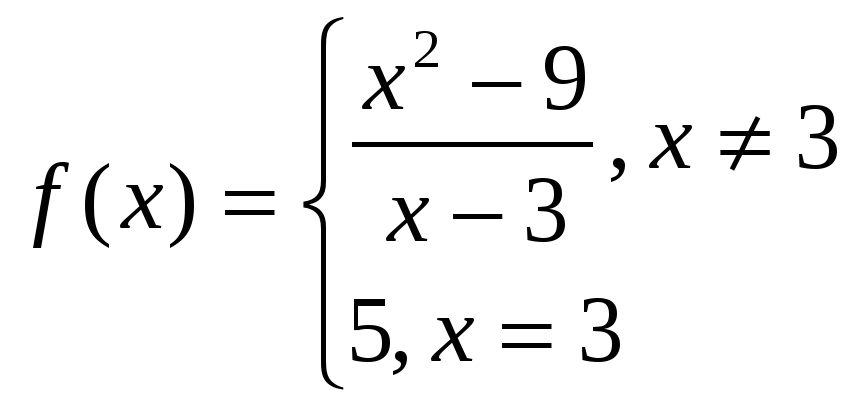 .
.
Вычислить производные.
1). ![]() 2).
2). ![]() 3).
3). ![]() .
.
4. Найти интеграл.
1). ![]() .
.
5. Найти интегралы методом замены переменной.
1) ![]() 2).
2). ![]() .
.
С-2. Обыкновенные дифференциальные уравнения.
Найти общее решение дифференциального уравнения.
1). ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() .
.
2. Найти частное решение дифференциального уравнения.
![]() .
.
С-3. Ряды.
Исследовать на сходимость ряд, используя признак Даламбера.
1). ![]() 2)
2) ![]() 3)
3) ![]() .
.
Исследовать на сходимость ряд, используя признак Лейбница.
1). ![]() 2).
2). ![]() .
.
3. Разложить в ряд Маклорена функцию.
![]() .
.
С-4. Вероятность. Теорема сложения вероятностей.
Из разрезной азбуки составлено слово «алфавит». Мальчик перемешал буквы, а потом составил их наугад. Какова вероятность того, что он опять составил это слово?
Карточка «Спортлото» содержит 36 чисел. В тираже участвует 5 чисел. Какова вероятность того, что верно будет угадано 5 чисел?
В каждом их трех ящиков по 100 деталей. В первом 80, во втором 70, в третьем 60 стандартных. Какова вероятность того, что все три детали вынутые из каждого ящика по одной, окажутся стандартными?
Вычислить:
 .
.
С-5. Случайная величина, ее функция распределения.
По мишени производится 3 выстрела, причем вероятность попадания при каждом выстреле 0,8. Рассматривается случайная величина Х – число попаданий в мишень. Найти закон распределения.
Вероятность попадания при стрельбе в цель 0,6. Найти закон распределения общего числа попаданий, если будет произведено 10 выстрелов.
С-6. Нахождение математического ожидания, дисперсии и среднего квадратично го отклонения дискретной случайной величины, заданной законом распределении.
1). Найти математическое ожидание М(х2), М(х+у), М(2у).
2). Найти дисперсию Д(х) по формуле Д(х)=М(х-М(х))2, Д(у) по формуле Д(у)=М(х2)-М2(х).
3). Найти среднее квадратичное отклонение случайных величин х и у.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| р | 0,1 | 0,1 | 0,1 | 0,09 | 0,3 | 0,009 | 0,3 | 0,001 |
| У | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| р | 0,001 | 0.2 | 0,001 | 0,3 | 0,006 | 0 | 0,09 | 0,4 |
С-7. Численное интегрирование.
Дан интеграл ![]() . Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
. Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
С-8. Нахождение производных функции в точке х по заданной таблично функции y=f(x) методом численного дифференцирования.
Найти значения первой и второй производной по данным из таблицы.
| х | 0,8 | 1,2 | 1,6 | 2,0 | 2,4 | 2,8 | 3,2 | 3,6 |
| у(х) | 2,857 | 3,946 | 4,938 | 5,801 | 6,503 | 7,010 | 7,288 | 7,301 |
С-9. Нахождение значения функции с использованием метода Эйлера.
Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального уравнения у/=f(х;у), удовлетворяющего начальным условиям у(х0)=у0 на отрезке [a;b]; шаг h=0,1.Все вычисления вести с десятичными знаками.
Вариант 2.
С-1. Дифференциальное и интегральное исчисление.
Вычисление пределов функции.
1). ![]() 2).
2). ![]() 3).
3). ![]() 4).
4). ![]() 5).
5). ![]() .
.
2. Исследовать функцию на непрерывность.
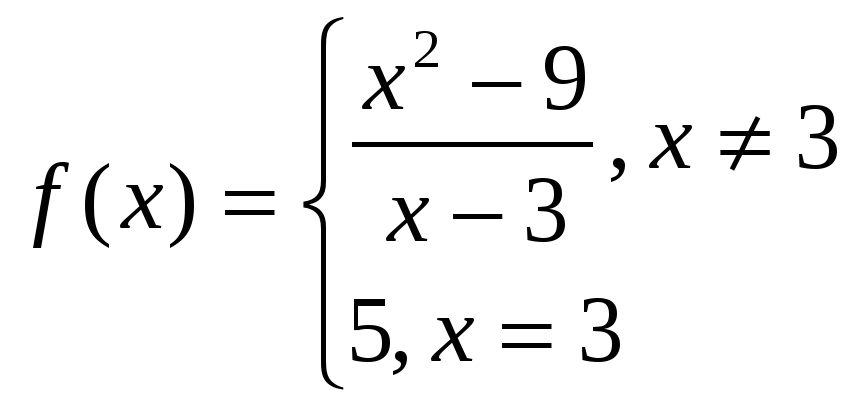 .
.
Вычислить производные.
1). ![]() 2).
2). ![]() 3).
3). ![]() .
.
4. Найти интеграл.
1). ![]() .
.
5. Найти интегралы методом замены переменной.
1) ![]() 2).
2). ![]() .
.
С-2. Обыкновенные дифференциальные уравнения.
Найти общее решение дифференциального уравнения.
1). ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() .
.
2. Найти частное решение дифференциального уравнения.
![]() .
.
С-3. Ряды.
Исследовать на сходимость ряд, используя признак Даламбера.
1). ![]() 2)
2) ![]() 3)
3) ![]() .
.
Исследовать на сходимость ряд, используя признак Лейбница.
1). ![]() 2).
2). ![]() .
.
3. Разложить в ряд Маклорена функцию.
![]() .
.
С-4. Вероятность. Теорема сложения вероятностей.
Из разрезной азбуки составлено слово «алфавит». Мальчик перемешал буквы, а потом составил их наугад. Какова вероятность того, что он опять составил это слово?
Карточка «Спортлото» содержит 36 чисел. В тираже участвует 5 чисел. Какова вероятность того, что верно будет угадано 5 чисел?
В каждом их трех ящиков по 100 деталей. В первом 80, во втором 70, в третьем 60 стандартных. Какова вероятность того, что все три детали вынутые из каждого ящика по одной, окажутся стандартными?
Вычислить:
 .
.
С-5. Случайная величина, ее функция распределения.
По мишени производится 3 выстрела, причем вероятность попадания при каждом выстреле 0,8. Рассматривается случайная величина Х – число попаданий в мишень. Найти закон распределения.
Вероятность попадания при стрельбе в цель 0,6. Найти закон распределения общего числа попаданий, если будет произведено 10 выстрелов.
С-6. Нахождение математического ожидания, дисперсии и среднего квадратично го отклонения дискретной случайной величины, заданной законом распределении.
1). Найти математическое ожидание М(х2), М(х+у), М(2у).
2). Найти дисперсию Д(х) по формуле Д(х)=М(х-М(х))2, Д(у) по формуле Д(у)=М(х2)-М2(х).
3). Найти среднее квадратичное отклонение случайных величин х и у.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| р | 0,1 | 0,1 | 0,1 | 0,09 | 0,3 | 0,009 | 0,3 | 0,001 |
| У | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| р | 0,001 | 0.2 | 0,001 | 0,3 | 0,006 | 0 | 0,09 | 0,4 |
С-7. Численное интегрирование.
Дан интеграл ![]() . Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
. Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
С-8. Нахождение производных функции в точке х по заданной таблично функции y=f(x) методом численного дифференцирования.
Найти значения первой и второй производной по данным из таблицы.
| х | 0,8 | 1,2 | 1,6 | 2,0 | 2,4 | 2,8 | 3,2 | 3,6 |
| у(х) | 2,857 | 3,946 | 4,938 | 5,801 | 6,503 | 7,010 | 7,288 | 7,301 |
С-9. Нахождение значения функции с использованием метода Эйлера.
Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального уравнения у/=f(х;у), удовлетворяющего начальным условиям у(х0)=у0 на отрезке [a;b]; шаг h=0,1.Все вычисления вести с десятичными знаками.
Вариант 3.
С-1. Дифференциальное и интегральное исчисление.
Вычисление пределов функции.
1). ![]() 2).
2). ![]() 3).
3). ![]() 4).
4). ![]() 5).
5). ![]() .
.
2. Исследовать функцию на непрерывность.
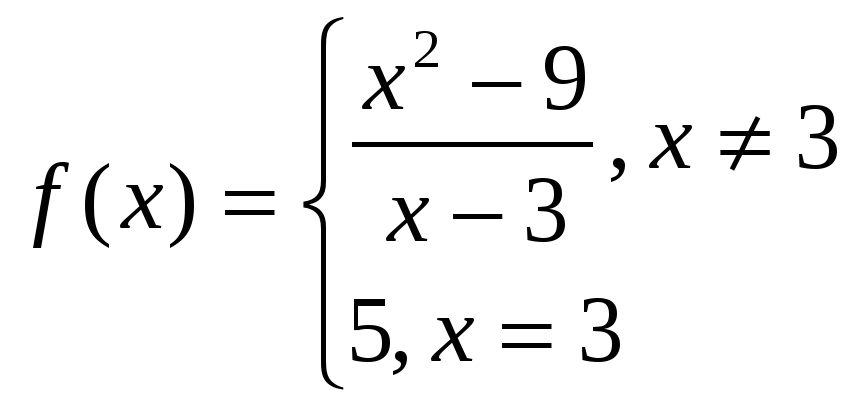 .
.
Вычислить производные.
1). ![]() 2).
2). ![]() 3).
3). ![]() .
.
4. Найти интеграл.
1). ![]() .
.
5. Найти интегралы методом замены переменной.
1) ![]() 2).
2). ![]() .
.
С-2. Обыкновенные дифференциальные уравнения.
Найти общее решение дифференциального уравнения.
1). ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() .
.
2. Найти частное решение дифференциального уравнения.
![]() .
.
С-3. Ряды.
Исследовать на сходимость ряд, используя признак Даламбера.
1). ![]() 2)
2) ![]() 3)
3) ![]() .
.
Исследовать на сходимость ряд, используя признак Лейбница.
1). ![]() 2).
2). ![]() .
.
3. Разложить в ряд Маклорена функцию.
![]() .
.
С-4. Вероятность. Теорема сложения вероятностей.
Из разрезной азбуки составлено слово «алфавит». Мальчик перемешал буквы, а потом составил их наугад. Какова вероятность того, что он опять составил это слово?
Карточка «Спортлото» содержит 36 чисел. В тираже участвует 5 чисел. Какова вероятность того, что верно будет угадано 5 чисел?
В каждом их трех ящиков по 100 деталей. В первом 80, во втором 70, в третьем 60 стандартных. Какова вероятность того, что все три детали вынутые из каждого ящика по одной, окажутся стандартными?
Вычислить:
 .
.
С-5. Случайная величина, ее функция распределения.
По мишени производится 3 выстрела, причем вероятность попадания при каждом выстреле 0,8. Рассматривается случайная величина Х – число попаданий в мишень. Найти закон распределения.
Вероятность попадания при стрельбе в цель 0,6. Найти закон распределения общего числа попаданий, если будет произведено 10 выстрелов.
С-6. Нахождение математического ожидания, дисперсии и среднего квадратично го отклонения дискретной случайной величины, заданной законом распределении.
1). Найти математическое ожидание М(х2), М(х+у), М(2у).
2). Найти дисперсию Д(х) по формуле Д(х)=М(х-М(х))2, Д(у) по формуле Д(у)=М(х2)-М2(х).
3). Найти среднее квадратичное отклонение случайных величин х и у.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| р | 0,1 | 0,1 | 0,1 | 0,09 | 0,3 | 0,009 | 0,3 | 0,001 |
| У | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| р | 0,001 | 0.2 | 0,001 | 0,3 | 0,006 | 0 | 0,09 | 0,4 |
С-7. Численное интегрирование.
Дан интеграл ![]() . Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
. Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
С-8. Нахождение производных функции в точке х по заданной таблично функции y=f(x) методом численного дифференцирования.
Найти значения первой и второй производной по данным из таблицы.
| х | 0,8 | 1,2 | 1,6 | 2,0 | 2,4 | 2,8 | 3,2 | 3,6 |
| у(х) | 2,857 | 3,946 | 4,938 | 5,801 | 6,503 | 7,010 | 7,288 | 7,301 |
С-9. Нахождение значения функции с использованием метода Эйлера.
Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального уравнения у/=f(х;у), удовлетворяющего начальным условиям у(х0)=у0 на отрезке [a;b]; шаг h=0,1.Все вычисления вести с десятичными знаками.
Вариант 4.
С-1. Дифференциальное и интегральное исчисление.
Вычисление пределов функции.
1). ![]() 2).
2). ![]() 3).
3). ![]() 4).
4). ![]() 5).
5). ![]() .
.
2. Исследовать функцию на непрерывность.
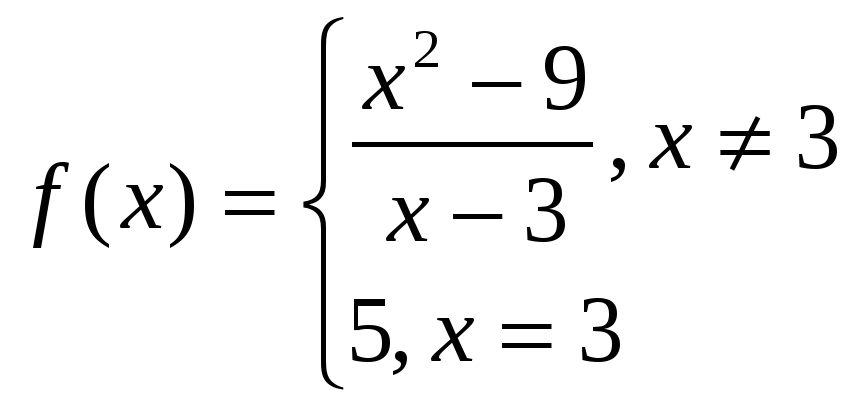 .
.
Вычислить производные.
1). ![]() 2).
2). ![]() 3).
3). ![]() .
.
4. Найти интеграл.
1). ![]() .
.
5. Найти интегралы методом замены переменной.
1) ![]() 2).
2). ![]() .
.
С-2. Обыкновенные дифференциальные уравнения.
Найти общее решение дифференциального уравнения.
1). ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() .
.
2. Найти частное решение дифференциального уравнения.
![]() .
.
С-3. Ряды.
Исследовать на сходимость ряд, используя признак Даламбера.
1). ![]() 2)
2) ![]() 3)
3) ![]() .
.
Исследовать на сходимость ряд, используя признак Лейбница.
1). ![]() 2).
2). ![]() .
.
3. Разложить в ряд Маклорена функцию.
![]() .
.
С-4. Вероятность. Теорема сложения вероятностей.
Из разрезной азбуки составлено слово «алфавит». Мальчик перемешал буквы, а потом составил их наугад. Какова вероятность того, что он опять составил это слово?
Карточка «Спортлото» содержит 36 чисел. В тираже участвует 5 чисел. Какова вероятность того, что верно будет угадано 5 чисел?
В каждом их трех ящиков по 100 деталей. В первом 80, во втором 70, в третьем 60 стандартных. Какова вероятность того, что все три детали вынутые из каждого ящика по одной, окажутся стандартными?
Вычислить:
 .
.
С-5. Случайная величина, ее функция распределения.
По мишени производится 3 выстрела, причем вероятность попадания при каждом выстреле 0,8. Рассматривается случайная величина Х – число попаданий в мишень. Найти закон распределения.
Вероятность попадания при стрельбе в цель 0,6. Найти закон распределения общего числа попаданий, если будет произведено 10 выстрелов.
С-6. Нахождение математического ожидания, дисперсии и среднего квадратично го отклонения дискретной случайной величины, заданной законом распределении.
1). Найти математическое ожидание М(х2), М(х+у), М(2у).
2). Найти дисперсию Д(х) по формуле Д(х)=М(х-М(х))2, Д(у) по формуле Д(у)=М(х2)-М2(х).
3). Найти среднее квадратичное отклонение случайных величин х и у.
| Х | -1 | -2 | -3 | -10 | -12 | -20 | -30 | -40 |
| р | 0,1 | 0,1 | 0,1 | 0,09 | 0,3 | 0,009 | 0,3 | 0,001 |
| У | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| р | 0,001 | 0.2 | 0,001 | 0,3 | 0,006 | 0 | 0,09 | 0,4 |
С-7. Численное интегрирование.
Дан интеграл ![]() . Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
. Вычислите приближенное значение этого интеграла по формулам прямоугольника, трапеции и формуле Симпсона при n=10 и с тремя знаками после запятой.
С-8. Нахождение производных функции в точке х по заданной таблично функции y=f(x) методом численного дифференцирования.
Найти значения первой и второй производной по данным из таблицы.
| х | 0,8 | 1,2 | 1,6 | 2,0 | 2,4 | 2,8 | 3,2 | 3,6 |
| у(х) | 2,857 | 3,946 | 4,938 | 5,801 | 6,503 | 7,010 | 7,288 | 7,301 |
С-9. Нахождение значения функции с использованием метода Эйлера.
Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального уравнения у/=f(х;у), удовлетворяющего начальным условиям у(х0)=у0 на отрезке [a;b]; шаг h=0,1.Все вычисления вести с десятичными знаками.
К о н т р о л ь н ы е р а б о т ы.
Контрольная работа 1.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Дидактические материалы (202.5 KB)
Дидактические материалы (202.5 KB)
 0
0 248
248 2
2 Нравится
0
Нравится
0




