Обучение математике в средней школе должно иметь своей главной целью развитие способностей к получению математических знаний. Главное для школьного образования – научить учиться и развить интеллект учащегося.
«Обратные тригонометрические функции» являются одной из наиболее эффективных тем школьного курса математики для развития математических способностей учащихся. Однако их изучение представляет для учащихся большие трудности.
Основной проблемой является недостаточная наглядность, а в результате и доступность, материала. Также трудность возникает в том, что учащиеся непрофильных классов ограничены по времени, им выделено недостаточное количество часов на прочное закрепление полученных знаний. Ученики же профильных классов зачастую сталкиваются с непониманием свойств обратных тригонометрических функций, ввиду неправильного представления их графических интерпретаций.
Несмотря на то, что сейчас многие школы хорошо оснащены и компьютеризированы, зачастую учителя не пользуются экранами и интерактивными досками из-за отсутствия готовых демонстрационных моделей для работы на уроках и пособий для их создания. Между тем, существует бесплатная и удобная в использовании программа GeoGebra, позволяющая решить эту проблему.
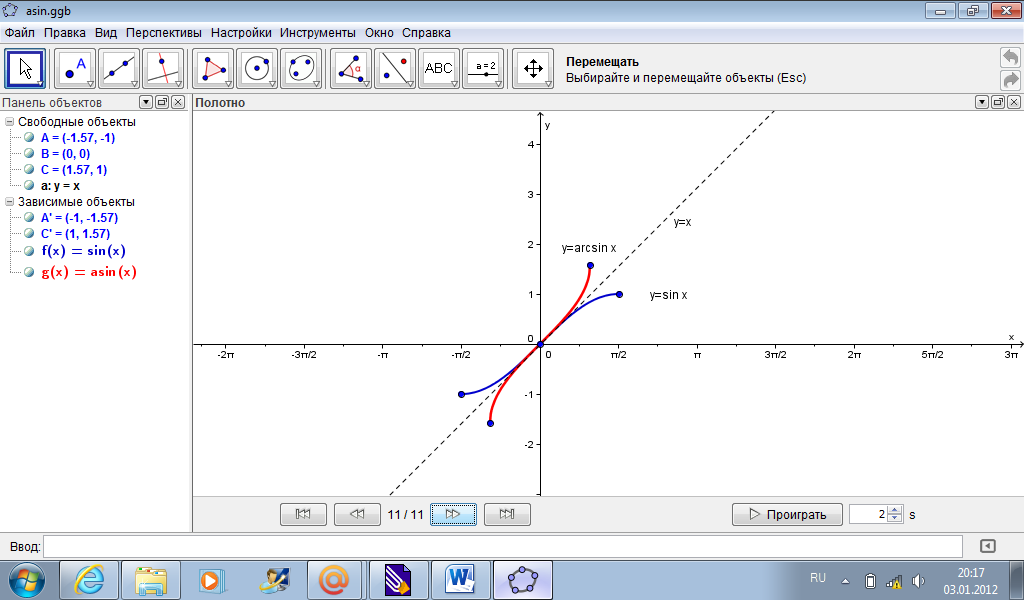
Рассмотрим пример построения графика функции y=arcsin х с помощью данной программы и фрагмент урока в 10 классе с использованием данной модели.
Построение графика функции y=arcsin х
Программа GeoGebra является бесплатной, установить ее можно с помощью сайта http://www.geogebra.org/cms/.
Перед началом построения необходимо подготовить полотно:
- Перспективы → Алгебра и графики.
- Настройки → Настройки. Выбрать следующее (рис. 1):
Далее переходим к построению.
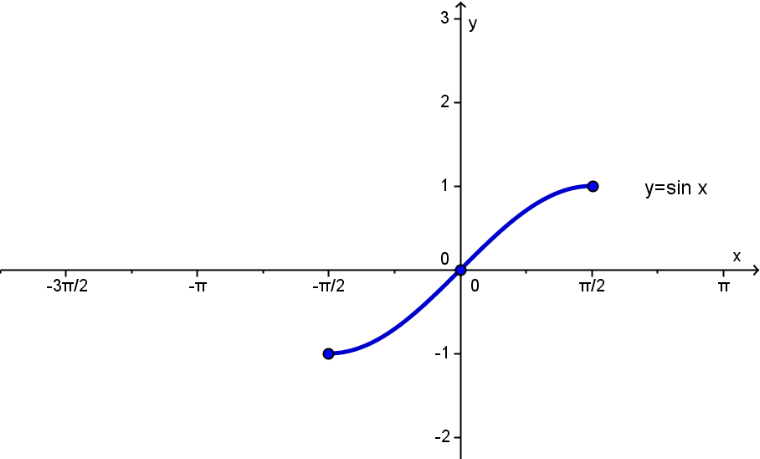
1) Строим график функции y=sin x x∈ [-п/2; п/2]. Для этого вводим точки:
(-п/2; -1), (0;0), (п/2; 1)
2) Соединяем точки плавной линией. Вводим:
Функция [y=sin(x), -п/2, п/2]
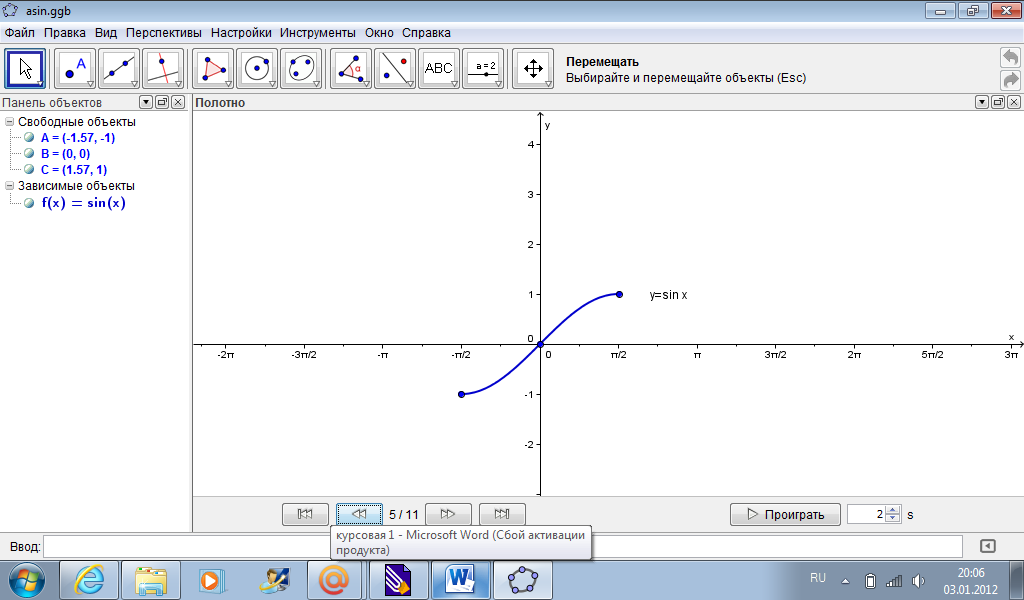
С помощью кнопки «Надпись», введем название полученного графика.

Задав в свойствах цвет и толщину линии, получим:
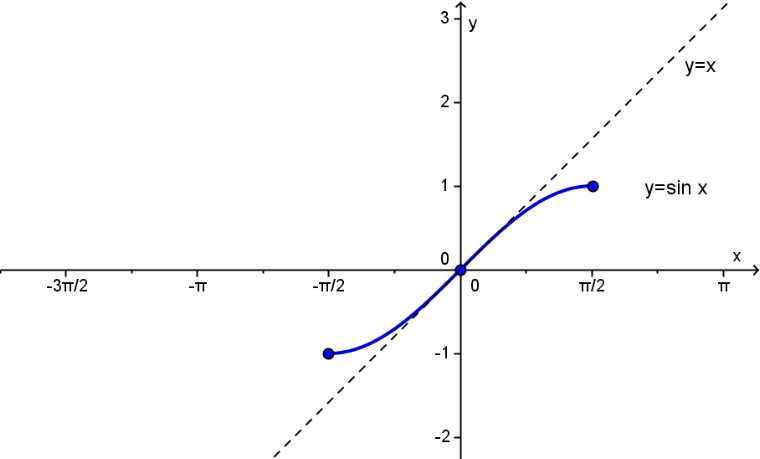
3) Построим теперь биссектрису первой и третьей четверти. Вводим
у=х
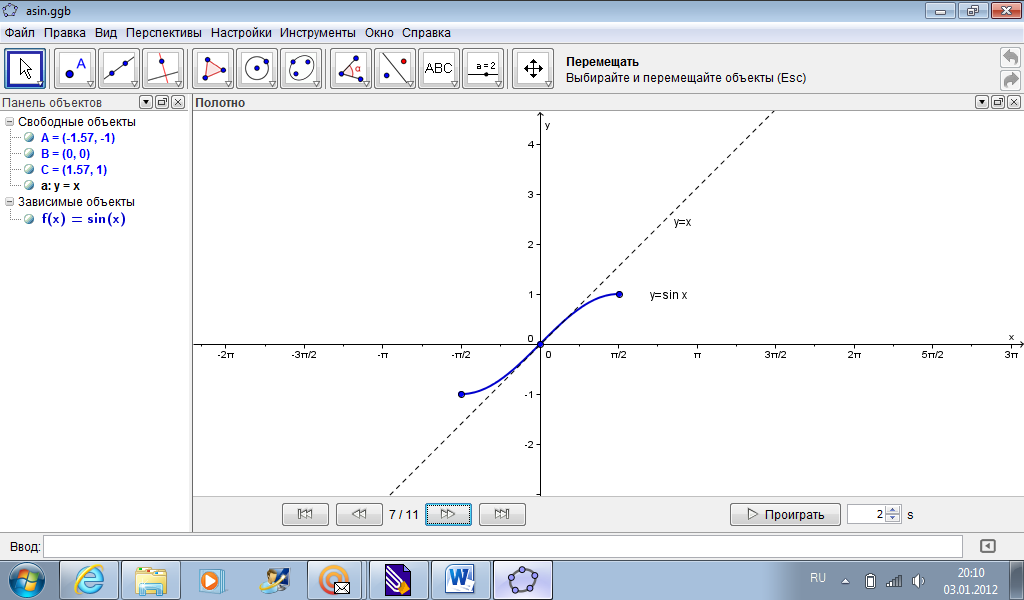
Выберем стиль построенной линии – пунктир.
Подпишем название построенной прямой (рис. 4).
4) Произведем симметрию графика y=sin x относительно прямой y=x.
Для этого, с помощью кнопки «Отражение относительно прямой», отразим три опорные точки (рис. 5):
Получим:
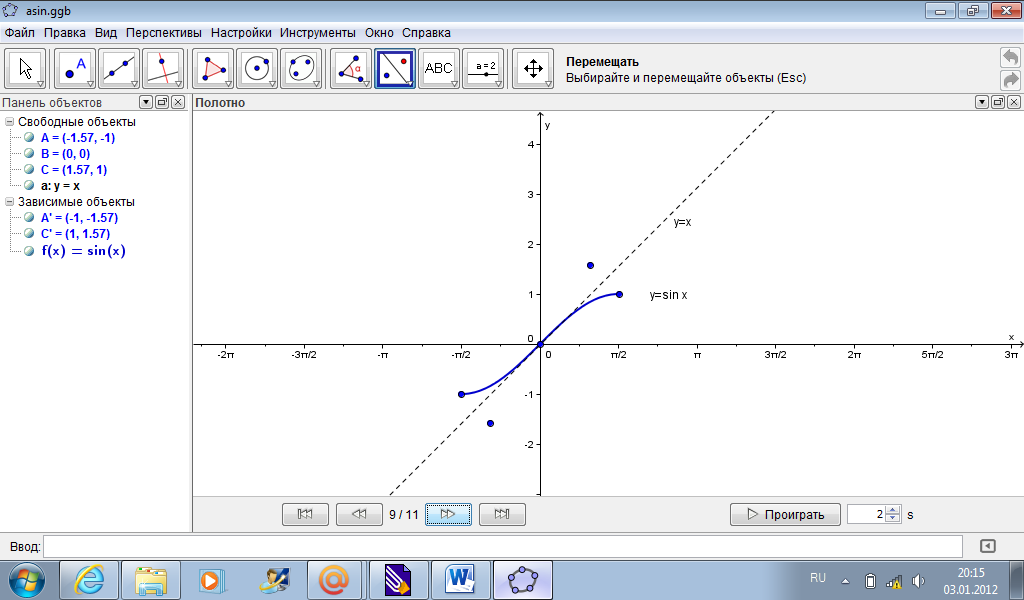
5) Соединим полученные точки. Введем:
Функция [asin(x), 1,1]
Полученную линию подпишем и выделим цветом (рис. 7):
Рассмотрим возможность использования данной модели на уроке математики в 10 классе при изучении нового материала. Тема урока: «Обратные тригонометрические функции. Арксинус, арккосинус».
1. Изучение нового материала. (15 мин.)
Ранее мы с вами познакомились с функцией y=sin x. Она монотонна и принимает все значения от – 1 до 1 на каждом из следующих отрезков: [-п/2; п/2], [п/2; 3п/2] и т.д. Значит, по теореме об обратной функции, на каждом из указанных промежутков данная функция имеет обратную функцию. Отметим, что это различные функции, среди них предпочтение отдают той, которая определена на отрезке [-п/2; п/2]. Построим ее график.
Изобразите в тетрадях координатную плоскость, отметьте направления и названия осей, начало координат и единичные отрезки по осям.
На отрезке [-п/2; п/2] начинаем строить синусоиду.
Составим таблицу.
Соединим точки плавной линией.
Начинаем строить график обратной функции. Для этого построим прямую y=x пунктирной линией.
Произведем симметрию синусоиды относительно прямой y=x.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



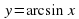 с помощью данной программы и фрагмент урока в 10 классе с использованием данной модели.
с помощью данной программы и фрагмент урока в 10 классе с использованием данной модели.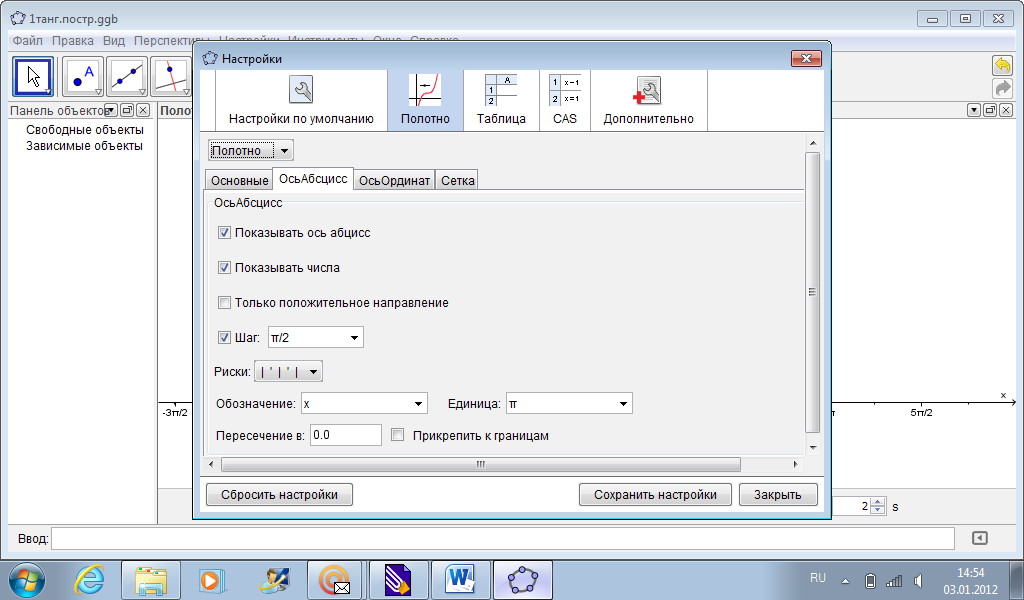
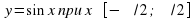 . Для этого вводим точки:
. Для этого вводим точки: 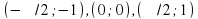

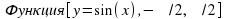
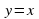
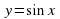 относительно прямой
относительно прямой 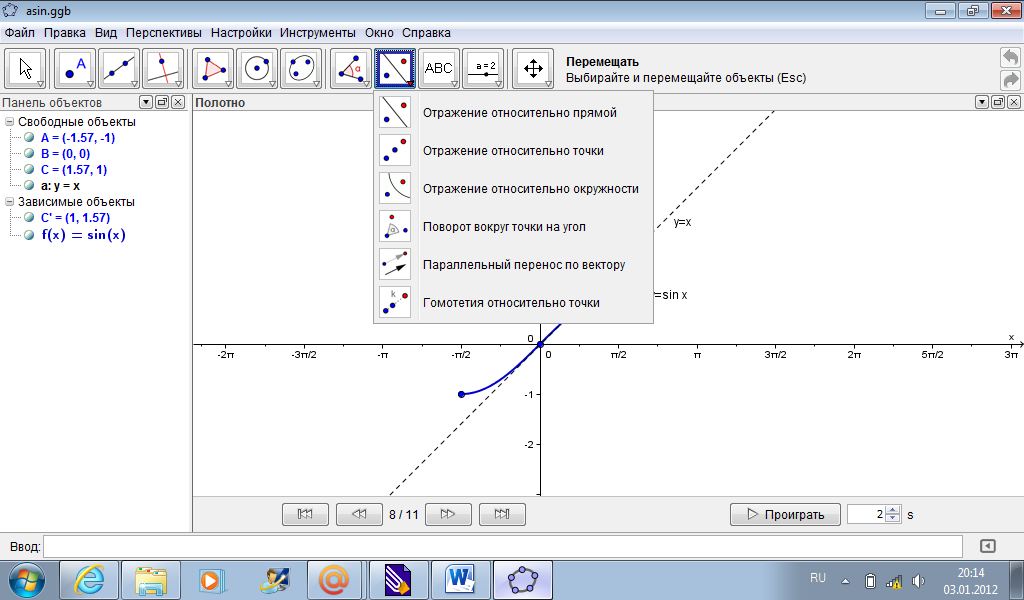
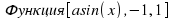
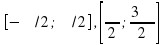 и т.д. Значит, по теореме об обратной функции, на каждом из указанных промежутков данная функция имеет обратную функцию. Отметим, что это различные функции, среди них предпочтение отдают той, которая определена на отрезке
и т.д. Значит, по теореме об обратной функции, на каждом из указанных промежутков данная функция имеет обратную функцию. Отметим, что это различные функции, среди них предпочтение отдают той, которая определена на отрезке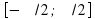 . Построим ее график.
. Построим ее график.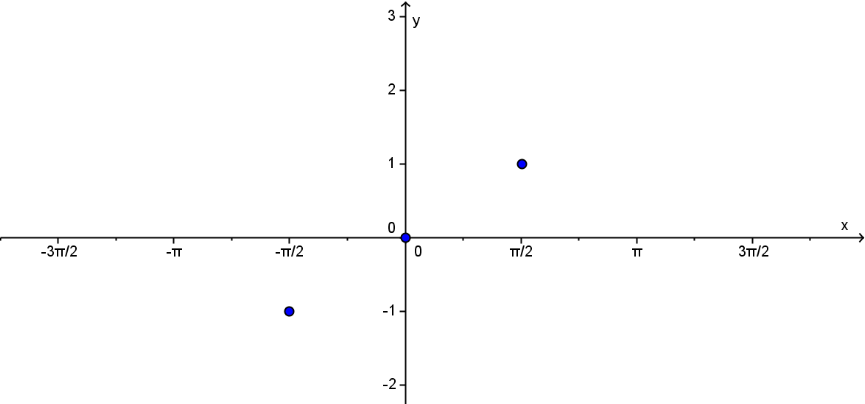









 Материал на тему "Использование программы Geogebra на уроках математики при изучении обратных тригонометрических функций" (0.64 MB)
Материал на тему "Использование программы Geogebra на уроках математики при изучении обратных тригонометрических функций" (0.64 MB)
 0
0 1423
1423 142
142 Нравится
0
Нравится
0


