Пособие по теме Последовательности

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для самостоятельной работы студентов

По дисциплине: МАТЕМАТИКА (включая алгебру и начала математического анализа; геометрию)

Тема: «Последовательности»

Специальность: 34.02.01 Сестринское дело Курс: 1

(базовой подготовки)

Купино

2020

Рассмотрено на заседании предметной цикловой

Методической комиссии по общеобразовательным дисциплинам,

общему гуманитарному и социально-экономическому, математическому и

естественно-научному циклу

Протокол № _____ от «_____» _________20____г.

Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.

Купино

2020 г

Пояснительная записка к методическому пособию

Методическое пособие предназначено для повторения теоретических и практических знаний по теме.

Цель пособия – повторить понятия последовательности, арифметической и геометрической последовательностей, формулы n-го члена, суммы первых n-членов этих последовательностей и подготовится к занятию по теме «Последовательности».

Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Последовательности, тест для самоконтроля и критерии оценки теста.

Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.

Последовательности

Определение числовой последовательности

Если х принимает только натуральные значения ( ), то имеем частный случай, а именно числовую последовательность.

Напомним, что натуральными являются числа 1, 2, 3, …, n, …

Функцию  , где  , называют функцией натурального аргумента, или числовой последовательностью, и обозначают следующим образом:  или  , или  .

Поясним, что обозначает, например, запись  .

–это значение функции, когда n=1, т. е.  .

 –это значение функции, когда n=2, т. е.   и т. д. …

 –это значение функции, когда аргумент равен n, т. е.  .

Примеры последовательностей

1.  - это формула общего члена. Задаем различные значения n, получаем различные значения у – членов последовательности.

, когда n=1;  , когда n=2 и т. д.,  .

Числа   являются членами заданной последовательности, а точки  лежат на гиперболе – графике функции   (см. Рис.4).

2. .

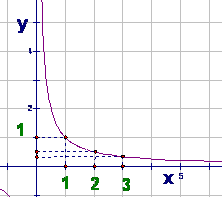
Рис. 4. График функции 

Если n=1, то  ; если n=2, то  ; если n=3, то  и т. д.

Ч исла   являются членами заданной последовательности, а точки  лежат на параболе - графике функции   (см. Рис.5).

Рис. 5. График функции 

3. .

Рис. 6. График функции 

Если n=1, то  ; если n=2, то  ; если n=3, то  и т. д.

Числа   являются членами заданной последовательности, а точки  лежат на прямой - графике функции   (см. Рис.6).

Аналитический способ задания последовательности

Существует три способа задания последовательностей: аналитический, словесный и рекуррентный. Рассмотрим каждый из них подробно.

Последовательность задана аналитически, если указана формула ее n-го члена  .

Рассмотрим несколько примеров.

1. Найти несколько членов последовательности, которая задана формулой n-го члена:   (аналитический способ задания последовательности).

Решение. Если n=1, то  ; если n=2, то  ; если n=3, то  и т. д.

Для заданной последовательности найдем   и  .

Решение.

.

.

2. Рассмотрим последовательность, заданную формулой n-го члена:  (аналитический способ задания последовательности).

Найдем несколько членов этой последовательности.

Если n=1, то  ; если n=2, то  ; если n=3, то  и т. д.

Вообще нетрудно понять, что членами этой последовательности являются те числа, которые при делении на 4 дают в остатке 1.

а. Для заданной последовательности найти  .

Решение:  . Ответ:  .

б. Даны два числа: 821, 1282. Являются ли эти числа членами заданной последовательности?

Решение:

Для того чтобы число 821 было членом последовательности, необходимо, чтобы выполнялось равенство:   или  . Последнее равенство является уравнением относительно n. Если решением данного уравнения является натуральное число, то ответ положительный.

В данном случае это так.  .

Ответ: да, 821 – член заданной последовательности,  .

Переходим ко второму числу. Аналогичные рассуждения приводят нас к решению уравнения:  .

Далее: 

Ответ: поскольку n не является натуральным числом, то число 1282 не является членом заданной последовательности.

Формулы, которые аналитически задают последовательность, могут быть самыми разными: простыми, сложными и т. д. Требование к ним одно: каждому значению n должно соответствовать единственное число.

3. Дано: последовательность задана следующей формулой  .

Найти три первых члена последовательности.

Решение.

,  ,  .

Ответ:  ,  ,  .

4. Являются ли числа   членами последовательности  ?

Решение:

а.  , т. е.  . Решая это уравнение, получаем, что  . Это натуральное число.

Ответ: первое заданное число является членом данной последовательности, а именно пятым ее членом.

б.  , т. е.  . Решая это уравнение, получаем, что  . Это натуральное число.

Ответ: второе заданное число тоже является членом данной последовательности, а именно девяносто девятым ее членом.

Словесный способ задания последовательности

Мы рассмотрели аналитический способ задания числовой последовательности. Он удобный, распространенный, но не единственный.

Следующий способ – это словесное задание последовательности.

Последовательность, каждый ее член, возможность вычисления каждого ее члена можно задать словами, не обязательно формулами.

Пример. Последовательность простых чисел.

Напомним, что простое число – это такое натуральное число, которое имеет ровно два различных делителя: 1 и само это число. Простыми являются числа 2, 3, 5, 7, 11, 13, 17, 19, 23 и т. д.

Их бесчисленное множество. Еще Евклид доказал, что последовательность этих чисел бесконечна, т. е. не существует самого большого простого числа. Последовательность задана, каждый член можно вычислить, утомительно, но можно вычислить. Эта последовательность задана словесно. Формулы, увы, не удается подобрать.

Пример . Рассмотрим число  =1,41421…

Это иррациональное число, десятичная его запись предусматривает бесконечное число цифр. Рассмотрим последовательность десятичных приближений числа по недостатку: 1; 1,4; 1,41; 1,414; 1,4142; и т. д.

Членов этой последовательности бесконечное множество, каждое из них можно вычислить. Задать эту последовательность формулой нельзя, поэтому описываем ее словесно.

Рекуррентный способ задания последовательности

Мы рассмотрели два способа задания числовой последовательности:

1. Аналитический способ, когда задается формула n-го члена.

2. Словесное задание последовательности.

И, наконец, существует рекуррентное задание последовательности, когда задаются правила вычисления n-го члена по предыдущим членам.

Рассмотрим

Пример. Последовательность Фибоначчи (13 век).

И сторическая справка:

Леона́рдо Пиза́нский (около 1170 года, Пиза — около 1250 года) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи (Fibonacci).

Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. «Книга абака» резко возвышается над европейской арифметико-алгебраической литературой XII—XIV вв. разнообразием и силой методов, богатством задач, доказательностью изложения. Последующие математики широко черпали из неё как задачи, так и приёмы их решения. По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления.

Задаются первые два члена   и каждый последующий член – это сумма двух предыдущих 

1; 1; 2; 3; 5; 8; 13; 21; 34; 55; … - первые несколько членов последовательности Фибоначчи.

Это последовательность задана рекуррентно, n-й член зависит от двух предыдущих.

Пример. Последовательность задается следующим образом: 

В этой последовательности каждый последующий член больше предыдущего на 2. Такая последовательность называется арифметической прогрессией.

Числа 1, 3, 5, 7 …- первые несколько членов этой последовательности.

Приведем еще один пример рекуррентного задания последовательности.

Пример. Последовательность задается следующим образом: 

Каждый последующий член этой последовательности получается умножением предыдущего члена на одно и то же число q. Такая последовательность имеет специальное название – геометрическая прогрессия. Арифметическая и геометрическая прогрессии будут объектами нашего изучения на следующих уроках.

Найдем несколько членов указанной последовательности при b=2 и q=3.

Числа 2; 6; 18; 54; 162 … - первые несколько членов этой последовательности.

Интересно, что эту последовательность можно задать и аналитическим способом, т. е. можно подобрать формулу. В данном случае формула будет таковой  .

Действительно: если n=1, то  ; если n=2, то  ; если n=3, то  и т. д.

Таким образом, мы констатируем: одна и та же последовательность может быть задана и аналитически и рекуррентно.

Предел последовательности

Введем еще одно важнейшее понятие - предел последовательности.

Определение. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера N. В этом случае пишут:    (читают: предел последовательности (уn) при стремлении n к бесконечности равен b, при этом часто фразу «при стремлении n к бесконечности» опускают). Используют и такую запись: уn → b(читают: уn стремится к b, или уn сходится к b).

Разъясним понятие «окрестность точки b». Под ним понимают интервал (b - r; b + r), где r - радиус окрестности (r  0).

Пример

Покажем, что 

Прежде всего отметим, что понятие предела последовательности очень сложное и с трудом воспринимается даже студентами. Поэтому подробно будем разбираться с этим примером (буквально по пунктам).

1. В данном случае число b = 0. Выберем произвольный радиус r окрестности точки b(обычно r выбирают небольшим и r  0). Поэтому будем рассматривать интервал (0 - r; 0 + r) или (-r; r).

2. Нужно найти номер N, начиная с которого все члены последовательности уn = 2/nбудут находиться в интервале (-r; r). Другими словами, надо относительно n решить неравенство –r n r.

3. Очевидно, что левая часть неравенства -r n выполняется при всех натуральныхn. Решим правую часть неравенства 2/n r. Получим 2 nr, откуда n  2/r. Итак, при n  2/n все члены последовательности уn отличаются от своего предела в менее чем на r.

4. Сделаем оценки. При r = 0,1 получаем n  20 (т. е. начиная с номера N = 21 все члены последовательности отличаются от предела не более чем на 0,1). При r = 0,01 имеем n  200 (т. е. начиная с номера N = 201 все члены последовательности отличаются от предела не более чем на 0,01) и т. д. На рисунке приведена графическая иллюстрация для этого случая.

Видно, что в r-окрестности предела собирается (сгущается) бесконечное множество членов последовательности, вне этой окрестности находится только конечное число членов.

Если последовательность (уn) имеет предел, то говорят, что она сходится, если не имеет предела - то расходится.

Теоремы о пределах и вычисление пределов последовательностей

Приведем формулировки теорем о пределах последовательностей.

Теорема 4.1. Если последовательность сходится, то только к одному пределу.

Теорема 4.2. Если последовательность сходится, то она ограничена.

Теорема 4.3. Если последовательность монотонна и ограничена, то она сходится.

Теорема 4.4. Если   то:

1) предел суммы равен сумме пределов: 

2) предел произведения равен произведению пределов: 

3) предел частного равен частному пределов: 

4) постоянный множитель можно вынести за знак предела: 

Теорема 4 используется при вычислении пределов последовательностей.

Пример Найдем пределы последовательностей: 

а) Используем теоремы 4.2 и 4.4 и получим: 

б) Применим теоремы 4.1 и 4.4. Имеем: 

в) Заметим, что сразу использовать теорему 4.3 нельзя, так как числитель 2n2 + 3 и знаменатель 5n2 - 1 дроби бесконечно большие величины и получаем что-то непонятное: ∞/∞. Поэтому разделим числитель и знаменатель дроби на n2 и используем теоремы 4.1, 4.3 и 4.4. Получим: 

г) Опять же сразу применять теоремы 4.3 и 4.1 нельзя. Тогда получим:   Каждое слагаемое в этой сумме стремится к нулю ( ), но в эту сумму входят n слагаемых, т. е. бесконечно большая величина.

Получаем опять нечто непонятное: 0 · ∞.

Учтем, что числитель дроби является суммой арифметической прогрессии и используем    теоремы 4.1, 4.3, 4.4. Имеем: 

д) При n → ∞ множитель   множитель   Возникает опять что-то непонятное: ∞ · 0. Поэтому умножим и разделим данное выражение на   и применим теоремы 4.1, 4.3, 4.4. Получаем: 

Таким образом, вычисление пределов последовательностей несложно, но необходимо проявлять внимание и аккуратность. При больших значениях n члены последовательности практически равны ее пределу.

Геометрическая прогрессия

Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк, когда сумма процентов начисляется на сумму, скопившуюся на счете за предыдущий период. Иными словами, если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на 7%, умноженному на 1,07. Ещё через год уже эта сумма увеличится на 7%, т.е. получившаяся в тот раз сумма вновь умножится на 1,07. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.

Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил 4 человек, те в свою очередь заразили еще по 4 человека, и таким образом вторая волна заражения – 16 человек, а те в свою очередь, заразили еще 4… и так далее…

Геометрической прогрессией называется числовая последовательность задаваемая двумя параметрами b, q (q ≠ 0) и законом  ,  , 

Число   называют знаменателем данной геометрической прогрессии.

• Если q 0 все члены геометрической прогрессии имеют один и тот же знак, совпадающий со знаком числа b.

• Если q  знаки членов геометрической прогрессии чередуются.

• В случае -1  прогрессию называют бесконечно убывающей геометрической прогрессией.