Понятие предела последовательности

10 класс. Предмет Алгебра и начало математического анализа.

Урок №34 дата19.01.2018г.

Тема урока: Понятие предела последовательности

Цель: привести основные понятия, связанные с последовательностями.

- обобщение знаний учащихся и формулировка определения числовой последовательности;
- изучение способов задания числовых последовательностей;
- совершенствование умений преобразования алгебраических выражений;
- развитие устных вычислительных навыков, математической речи учащихся, формирование аналитических и логических способностей, расширение кругозора;
- воспитание самостоятельности, интереса и уважения к изучаемому предмету.

Задача урока: подготовка учащихся к изучению темы «Пределы».

Тип урока : Изучение нового материала.

Оборудование: таблицы, плакаты, карточки.

Ход уроков

I. Сообщение темы и цели уроков 

II. Изучение нового материала

Определение 1. Функцию вида у = f(x), х ∈ N называют функцией натурального аргумента или числовой последовательностью и обозначают у = f(n), или у1, у2, у3, ...,уn, ..., или (уn). Также можно сказать, что числовой последовательностью называют множество чисел, для каждого из которых известен его порядковый номер.

Пример 1

а) Для последовательности положительных нечетных чисел 1, 3, 5, 7, ... - известно, что первое число равно 1, второе число равно 3, третье число равно 5 и т. д.

б) Для последовательности правильных дробей с числителем 1: 1/2, 1/3, 1/4, 1/5, ... - известно, что первое число равно 1/2, второе число равно 1/3, третье число равно 1/4 и т. д.

Числа, образующие последовательность, называют членами последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена: у1, у2, у3, ...,уn, ... . Соответственно, член последовательности с номером n (или n-й член последовательности) обозначают уn, а саму последовательность - (уn).

Пример 2

Рассмотрим последовательность натуральных трехзначных чисел: 100; 101; 102; ...; 999. В ней: у1 = 100, у2 = 101, у3 = 102, ..., y900 = 999. Член этой последовательности с номером n (n-й член последовательности) можно вычислить по формуле уn = 99 + n, гдеn = 1, 2, 3, ...,900.

1. Способы задания последовательностей

Последовательность необходимо задать, т. е. указать способ, с помощью которого можно найти каждый ее член. Рассмотрим основные способы задания последовательностей.

1. Аналитический способ (формула n-го члена)

Последовательность задается формулой, которая позволяет найти по номеру n ее член уn.

Пример 3

а) Пусть последовательность задана формулой уn = 3n - 2. Подставляя вместо n натуральные числа, находим члены последовательности:  и т. д. Имеем последовательность 1,4, 7,... .

б) Пусть последовательность задана формулой  Подставляя вместо nнатуральные числа, находим члены последовательности:  и т. д. Имеем последовательность 0, 1, 0, 1,... .

ФИЗКУЛЬТМИНУТКА (для глаз)

2. Аналитический способ (рекуррентная формула)

Последовательность задается формулой, которая позволяет найти следующие члены последовательности, если известны один или несколько предыдущих членов.

Пример 4

а) Пусть последовательность задана формулой уn+1 = 2уn + 3, где у1 = 5 и n ≥ 1.

Запишем рекуррентную формулу для n = 1: у1+1 = 2у1 + 3 или у2 = 2 · 5 + 3 = 13.

Запишем формулу для n = 2: у2+1 = 2у2 + 3 или у3 = 2 · 13 + 3 = 29.

Запишем формулу для n = 3: y3+1 = 2у3 + 3 или y4 = 2 · 29 + 3 = 61 и т. д.

Имеем последовательность 5, 13, 29, 61, ... .

б) Пусть последовательность задана формулой Уn+2 = 2уп+1 + 3уn, где у1 = 1, у2 = 2 и n ≥ 1.

Запишем рекуррентную формулу для n = 1: у1+2 = 2у1+1 + 3у1, или У3 = 2у2 + 3у1 или у3 = 2 · 2 + 3 · 1 = 7.

Запишем формулу для n = 2: у2+2 = 2у2+1 + 3у2 или у4 = 2у3 + 3у2 = 2 · 7 + 3 · 2 = 20.

Запишем формулу для n = 3: у3+2 = 2y3+1 + 3y3, или у5 = 2у4 + Зу3, или у5 = 2 · 20 + 3 · 7 = 61 и т. д.

Имеем последовательность 1, 2, 7, 20, 61, ... .

3. Описательный способ

Описывается способ получения членов последовательности.

Пример 5

а) Рассмотрим последовательность натуральных четных чисел. Из описания последовательности легко выписать ее члены: 2, 4, 6, 8,....

б) Рассмотрим последовательность приближений по недостатку с точностью до п цифр иррационального числа к. Из описания последовательности выписываем ее члены: 3; 3,1; 3,14; 3,141; 3,1415; ... .

2. Основные свойства последовательностей

Теперь рассмотрим два основных свойства последовательностей.

1. Ограниченность последовательности

Определение 2. Последовательность (уn) называют ограниченной сверху, если все ее члены не больше некоторого числа М, т. е. уn ≤ М. Число М называют верхней границей последовательности.

Пример 6

Последовательность уn = 5 - n ограничена сверху. При этом число М = 4. Покажем, что при всех натуральных n выполнено неравенство уn ≤ М. Получаем неравенство 5 - n ≤ 4, откуда n ≥ 1 (т. е. неравенство справедливо при всех n ∈ N).

Определение 3. Последовательность (уn) называют ограниченной снизу, если все ее члены не меньше числа m, т. е. уn ≥ m. Число m называют нижней границей последовательности.

Пример 7

Последовательность уn = 3 + 2n ограничена снизу. При этом число m = 5. Покажем, что при всех натуральных n выполнено неравенство yn ≥ m. Получаем неравенство 3 + 2n≥ 5, откуда n ≥ 1 (т. е. неравенство справедливо при всех n ∈ N).

Если последовательность ограничена и сверху и снизу, то ее называют ограниченной последовательностью. Иначе, последовательность (уn) называют ограниченной, если существуют два таких числа m и М, что для любого натурального номера n выполнено неравенство m ≤ уn ≤ М.

Пример 8

Докажем ограниченность последовательности 

Найдем первый член последовательности  и член последовательности с очень большим номером n, например  Возникает гипотеза, что последовательность ограничена, m = 0 и М = 1. Поэтому надо доказать, что при всех натуральных значениях n выполнено неравенство  Очевидно, что левая часть неравенства  выполняется. Рассмотрим правую часть неравенства  Так как выражение n + 2 положительно, то получаем неравенство n - 1 ≤ n + 2 или -1 ≤ 2, которое является верным.

2. Монотонность последовательности

Определение 4. Последовательность (уn) называют возрастающей, если каждый ее член (начиная со второго) больше предыдущего, т. е. уn+1  уn для n ≥ 1.

Определение 5. Последовательность (уn) называют убывающей, если каждый ее член (начиная со второго) меньше предыдущего, т. е. yn+1 n для n ≥ 1.

Пример 9

Определим монотонность последовательности 

Запишем (n + 1)-й член последовательности:  Найдем разность двух соседних членов:        Так как n- натуральное число, то при всех n дробь  положительна. Поэтому уn+1 – уn  0 или уn+1  уn при всех n. Тогда по определению данная последовательность (уn) возрастающая.

Заметим, что последовательность уn = an при a  1 возрастает, при 0 a 

3. Предел последовательности

Введем еще одно важнейшее понятие - предел последовательности.

Определение 6. Число b называют пределом последовательности (уn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера N. В этом случае пишут:   (читают: предел последовательности (уn) при стремлении n к бесконечности равен b, при этом часто фразу «при стремлении n к бесконечности» опускают). Используют и такую запись: уn → b(читают: уn стремится к b, или уn сходится к b).

Разъясним понятие «окрестность точки b». Под ним понимают интервал (b - r; b + r), где r - радиус окрестности (r  0).

Пример 10

Покажем, что 

Прежде всего отметим, что понятие предела последовательности очень сложное и с трудом воспринимается даже студентами. Поэтому подробно будем разбираться с этим примером (буквально по пунктам).

1. В данном случае число b = 0. Выберем произвольный радиус r окрестности точки b(обычно r выбирают небольшим и r  0). Поэтому будем рассматривать интервал (0 - r; 0 + r) или (-r; r).

2. Нужно найти номер N, начиная с которого все члены последовательности уn = 2/nбудут находиться в интервале (-r; r). Другими словами, надо относительно n решить неравенство –r n r.

3. Очевидно, что левая часть неравенства -r n выполняется при всех натуральныхn. Решим правую часть неравенства 2/n r. Получим 2 nr, откуда n  2/r. Итак, при n  2/n все члены последовательности уn отличаются от своего предела в менее чем на r.

4. Сделаем оценки. При r = 0,1 получаем n  20 (т. е. начиная с номера N = 21 все члены последовательности отличаются от предела не более чем на 0,1). При r = 0,01 имеем n  200 (т. е. начиная с номера N = 201 все члены последовательности отличаются от предела не более чем на 0,01) и т. д. На рисунке приведена графическая иллюстрация для этого случая.

Видно, что в r-окрестности предела собирается (сгущается) бесконечное множество членов последовательности, вне этой окрестности находится только конечное число членов.

Если последовательность (уn) имеет предел, то говорят, что она сходится, если не имеет предела - то расходится.

4. Теоремы о пределах и вычисление пределов последовательностей

Приведем формулировки теорем о пределах последовательностей.

Теорема 4.1. Если последовательность сходится, то только к одному пределу.

Теорема 4.2. Если последовательность сходится, то она ограничена.

Теорема 4.3. Если последовательность монотонна и ограничена, то она сходится.

Теорема 4.4. Если  то:

1) предел суммы равен сумме пределов: 

2) предел произведения равен произведению пределов: 

3) предел частного равен частному пределов: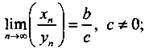 

4) постоянный множитель можно вынести за знак предела: 

Теорема 4 используется при вычислении пределов последовательностей.

Пример 11

Найдем пределы последовательностей: 

а) Используем теоремы 4.2 и 4.4 и получим: 

б) Применим теоремы 4.1 и 4.4. Имеем: 

в) Заметим, что сразу использовать теорему 4.3 нельзя, так как числитель 2n2 + 3 и знаменатель 5n2 - 1 дроби бесконечно большие величины и получаем что-то непонятное: ∞/∞. Поэтому разделим числитель и знаменатель дроби на n2 и используем теоремы 4.1, 4.3 и 4.4. Получим: 

г) Опять же сразу применять теоремы 4.3 и 4.1 нельзя. Тогда получим:  Каждое слагаемое в этой сумме стремится к нулю (), но в эту сумму входят n слагаемых, т. е. бесконечно большая величина.

Получаем опять нечто непонятное: 0 · ∞.

Учтем, что числитель дроби является суммой арифметической прогрессии и используем    теоремы 4.1, 4.3, 4.4. Имеем: 

д) При n → ∞ множитель  множитель  Возникает опять что-то непонятное: ∞ · 0. Поэтому умножим и разделим данное выражение на  и применим теоремы 4.1, 4.3, 4.4. Получаем: 

Таким образом, вычисление пределов последовательностей несложно, но необходимо проявлять внимание и аккуратность. При больших значениях n члены последовательности практически равны ее пределу.

III. Контрольные вопросы

1. Дайте определение последовательности.

2. Основные способы задания последовательности.

3. Ограниченность последовательности.

4. Монотонность последовательности.

5. Понятие r-окрестности точки Ь.

6. Определение предела последовательности.

7. Теоремы о пределах последовательности (фронтальный опрос).

IV. Задание на уроках

№4.25,№4.29,№ 4.35(а,б) (см. в тетради у учителя)

V. Задание на дом

 №4.35(в,г,д,е,ж,з,)

VI. Творческие задания

1. Найдите четыре первых члена последовательности (аn), если:

Ответы: а) а1 = 1, а2 = 2, a3 = 5, а4 = 14; б) а1 = 2, а2 = 11, а3 = 47, а4 = 191; в) а1 = 1, а2 = 2, а3 = 3, а4 = 5; г) а1 = 2, а2 = 1, a3 = -3, а4 = -5; д) а1 = 1, а2 = 2, а3 = 4, а4 = 8; е) a1 = 2, а2 = 1, а3 = 4, а4 = 9.

2. Докажите ограниченность последовательности (аn):

3. Определите монотонность последовательности (аn):

Ответы: а, д, ж) возрастающая; в, е) убывающая; б, г, з) немонотонная.

VII. Подведение итогов уроков

VIII Рефлексия

3