Подготовка к ЕГЭ. Задание № 16

ЕГЭ

Информатика и икт

Задание 16

разбор типовых задач

Автор: учитель информатики МБОУ «СОШ № 8» города Братска

Шаманская Светлана Владимировна

ПЕРВЫЙ ТИП ЗАДАНИЙ

Задание № 1. Решите уравнение 224 x + 1 10 = 101 8 .

Чтобы решить это уравнение, необходимо перевести числа, стоящие в правой и левой частях, в одну систему счисления. Представим все числа в десятичной системе счисления.

224 х =2  х 2 + 2  х 1 + 4  х 0 =(2х 2 + 2х + 4) 10

101 8 =1  8 2 + 0  8 1 + 1  8 0 =64+1 10 =65 10

Подставим в уравнение:

(2х 2 + 2х + 4) 10 + 1 10 =65 10

2х 2 + 2х - 60=0  х 2 + х - 30=0

Получили квадратное уравнение. Решаем его.

D=1+120=121

х 1 =(-1+11)/2=5 и х 2 = (-1-11)/2=-6

Так как х – это основание системы счисления и является натуральным числом (большим 1), то ответом будет число 5.

Ответ: 5

ПЕРВЫЙ ТИП ЗАДАНИЙ

Задание № 2. Решите уравнение 121 x + 1 10 = 101 7 . Ответ запишите в троичной системе счисления (основание системы счисления в ответе писать не нужно)

Чтобы решить это уравнение, необходимо перевести числа, стоящие в правой и левой частях, в одну систему счисления. Представим все числа в десятичной системе счисления.

121 х =1  х 2 + 2  х 1 + 1  х 0 =(х 2 + 2х + 1) 10

101 7 =1  7 2 + 0  7 1 + 1  7 0 =49+1 10 =50 10

Подставим в уравнение:

(х 2 + 2х + 1) 10 + 1 10 =50 10

х 2 + 2х -48=0

Получили квадратное уравнение. Решаем его.

D=4+192=196

х 1 =(-2+14)/2=6 и х 2 = (-2-14)/2=-8

Так как х – это основание системы счисления и является натуральным числом (большим 1), то ответом будет число 6.

Ответ необходимо записать в троичной системе счисления.

Ответ: 20

ВТОРОЙ ТИП ЗАДАНИЙ

Задание № 3. В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.

По условию число 18 дано в десятичной системе счисления. Если это число записать в другой (неизвестной нам) системе счисления, то получится число 30. Исходя из этих данных, можно составить уравнение:

18 10 =30 х

Чтобы решить это уравнение, необходимо перевести числа, стоящие в правой и левой частях, в одну систему счисления.

Представим число 30 х в десятичной системе счисления:

30 х =3  х 1 + 0  х 0 =3х 10

Подставим в правую часть уравнения:

18 10 =3х 10 .

Получили простое линейное уравнение, из которого получаем х=6.

Ответ: 6

ВТОРОЙ ТИП ЗАДАНИЙ

Задание № 4. В системе счисления с некоторым основанием десятичное число 23 записывается в виде 212. Укажите это основание.

По условию число 23 дано в десятичной системе счисления. Если это число записать в другой (неизвестной нам) системе счисления, то получится число 212. Исходя из этих данных, можно составить уравнение:

23 10 =212 х

Представим число 212 х в десятичной системе счисления:

212 х =2  х 2 + 1  х 1 + 2  х 0 =(2х 2 + х + 2) 10

Подставим в правую часть уравнения:

23 10 =(2х 2 + х + 2) 10 .

Получили квадратное уравнение. Решаем его.

23=2х 2 + х + 2  2х 2 + х -21=0

D=1+168=169

х 1 =(-1+13)/4=3 и х 2 = (-1-13)/4=-3,5

Так как х – это основание системы счисления и является натуральным числом, то ответом будет число 3.

Ответ: 3

ТРЕТИЙ ТИП ЗАДАНИЙ

Задание № 5. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Для решения этого задания необходимо вспомнить алгоритм перевода чисел из десятичной системы счисления в любую другую. Рассмотрим пример перевода числа 75 10 в систему счисления с основанием 4:

Получили 102 3 4 . Последняя цифра этого числа является остатком от первого деления числа 75 на основание системы счисления, в которую переводим число.

ТРЕТИЙ ТИП ЗАДАНИЙ

Нам дано десятичное число 23, при переводе его в неизвестную систему счисления получим число, оканчивающееся на цифру 2.

Рассмотрим подробнее начальный этап перевода числа 23.

В данном примере число 23 является делимым, х – делителем, а – неполным частным, 2 - остатком

ТРЕТИЙ ТИП ЗАДАНИЙ

Составим уравнение:

х  а+2=23

Перенесем известное в правую часть: х  а=21

Получили уравнение с двумя неизвестными, которое можно решить методом подбора. В левой части находится произведение двух целых чисел, соответственно правую часть также можно представить в виде произведения двух множителей.

21=1  21=3  7=7  3=21  1, где первый множитель - это предполагаемое основание системы счисления, а второй – неполное частное при делении.

1– не подходит, так как основание системы счисления не может быть равным 1

3 - подходит

7 - подходит

21 – подходит

Ответ: 3, 7, 21

ТРЕТИЙ ТИП ЗАДАНИЙ

Задание № 6. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Представим процесс перевода числа 71 из десятичной системы счисления в неизвестную - х

Отметим, что a и b должны быть натуральными числами. Также стоит рассмотреть частный случай, когда а=1, тогда b=0.

Составим уравнения:

х  а + 3 = 71

х  b + 1 = а

Подставим левую часть второго уравнения в первое вместо а, получим

х  (х  b + 1) + 3=71  х  (х  b + 1) =68

Так как в левой части полученного уравнения находится произведение двух множителей, то и справа тоже должно быть число, которое можно представить в виде произведения двух целых чисел.

ТРЕТИЙ ТИП ЗАДАНИЙ

68 = 1  68 = 2  34 = 4  17 = 17  4 = 34  2 = 68  1.

Рассмотрим все варианты:

1) 1  68 – не подходит, так как основание системы счисления не может быть равным 1;

2) 2  34 = х  (х  b + 1)

х=2 и 2b + 1=34  2b=33. Этот вариант также не подходит, так как значение b должно быть натуральным или равным 0

3) 4  17

х=4 и 4b + 1=17  4b=16  b=4. Этот вариант подходит.

4) 17  4

х=17 и 17b + 1=4  17b=3. Этот вариант не подходит, так как значение b должно быть натуральным или равным 0

5) 34  2

х=34 и 34b + 1=2  34b=1. Этот вариант также не подходит

6) 68  1

х=68 и 68b + 1=1  68b=0  b=0. Этот вариант подходит

Ответ: 4, 68

ЧЕТВЕРТЫЙ ТИП ЗАДАНИЙ

Задание № 7. Сколько единиц содержится в двоичной записи значения выражения 4 2018 +2 2018 -32

По условию задания необходимо вычислить значение выражения, затем перевести в двоичную систему счисления, в полученном числе посчитать количество единиц.

Чтобы вычислить значение выражения в десятичной системе счисления и перевести в двоичную, необходимо воспользоваться маленькой хитростью:

(2 10 ) 1 =2 10 =10 2

(2 10 ) 2 =4 10 =100 2

(2 10 ) 3 =8 10 =1000 2

(2 10 ) 4 =16 10 =10000 2

……………………………………………

В приведенных примерах прослеживается зависимость между степенью двойки в десятичной системе счисления и количеством нулей в двоичной записи числа.

Также для решения задания потребуется умение работать со степенями: 4 2018 =(2 2 ) 2018 =2 4036

ЧЕТВЕРТЫЙ ТИП ЗАДАНИЙ

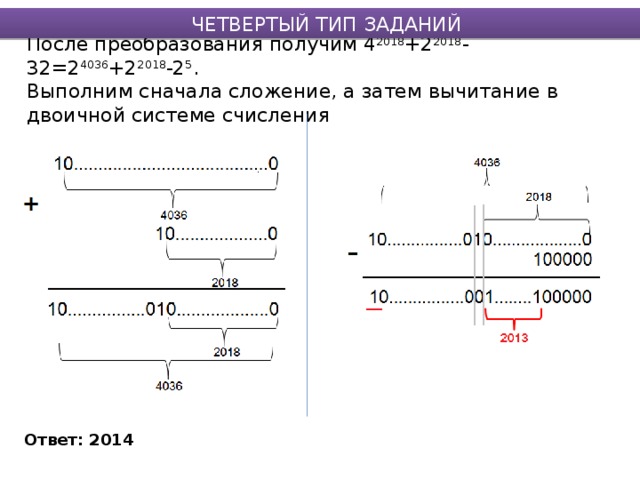
После преобразования получим 4 2018 +2 2018 -32=2 4036 +2 2018 -2 5 . Выполним сначала сложение, а затем вычитание в двоичной системе счисления

Ответ: 2014

ЧЕТВЕРТЫЙ ТИП ЗАДАНИЙ

Задание № 8. Значение выражения 9 8 +3 5 -9 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

Закономерность, которую мы рассмотрели в предыдущем примере, действует для любой системы счисления:

(3 10 ) 1 =3 10 =10 3

(3 10 ) 2 =9 10 =100 3

(3 10 ) 3 =27 10 =1000 3

(3 10 ) 4 =81 10 =10000 3

……………………………………………

В приведенных примерах прослеживается зависимость между степенью двойки в десятичной системе счисления и количеством нулей в двоичной записи числа.

Приведем выражение к степеням тройки:

9 8 +3 5 -9= 3 16 +3 5 -3 2

ЧЕТВЕРТЫЙ ТИП ЗАДАНИЙ

3 16 +3 5 -3 2 Сначала выполним сложение, затем вычитание в троичной системе счисления

Ответ: 3