Площадь треугольника

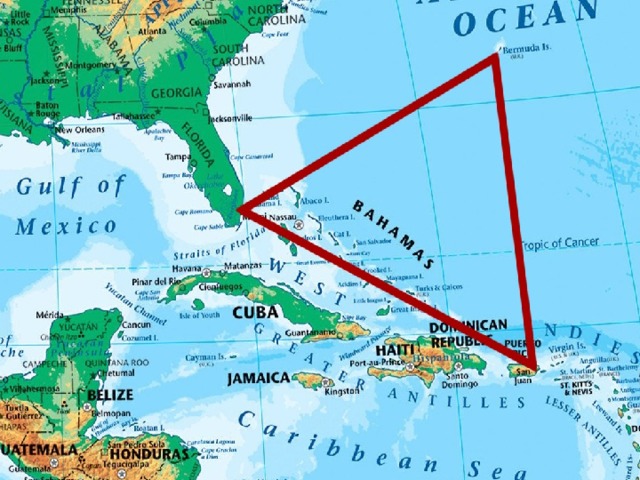
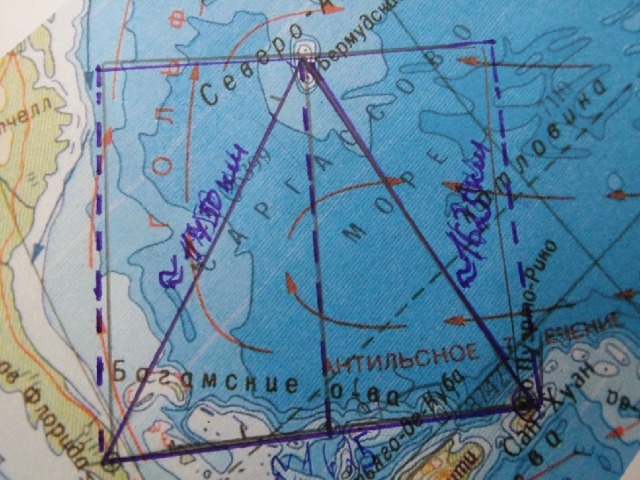
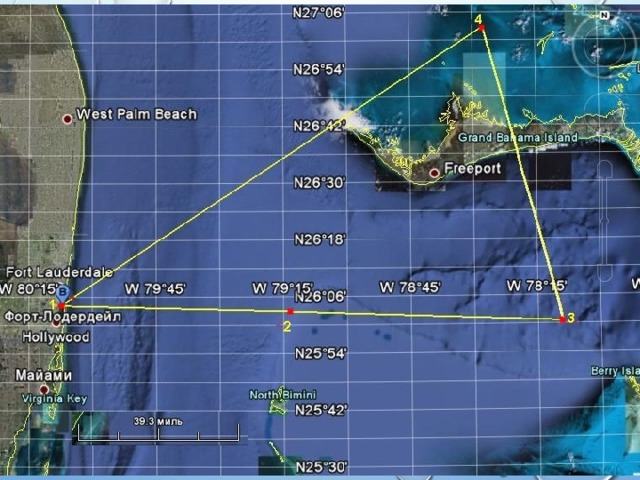
Бермудский треугольник — район в Атлантическом океане, ограниченный треугольником, вершинами которого являются Флорида, Бермудские острова и Пуэрто-Рико.

Вопрос урока: «Какова площадь Бермудского

треугольника?»

Цель урока

?

Узнать, как найти площадь треугольника

Задачи урока

• Познакомиться с формулой нахождения площади треугольника;
• Вычислить площадь Бермудского треугольника.

Площадь

треугольника

8 класс

Теорема. Площадь треугольника равна половине произведения его основания на высоту.

Дано: АВС;

СН- высота;

АВ- основание.

Доказать:

S= ½ ∙ АВ ∙ СН.

С

А

Н

В

5

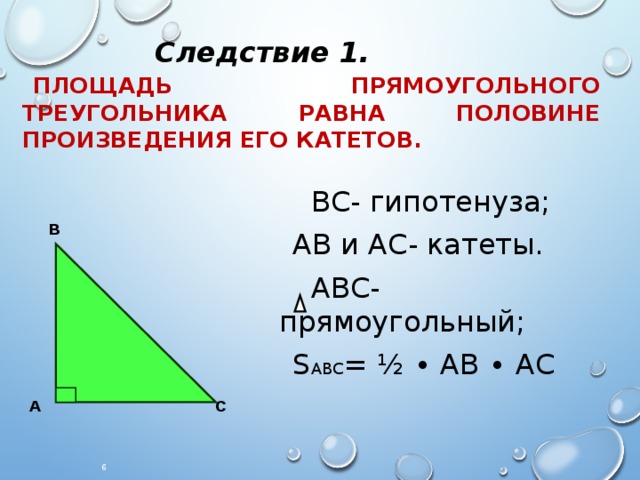
Следствие 1.

Площадь прямоугольного треугольника равна половине произведения его катетов.

ВС- гипотенуза;

АВ и АС- катеты.

АВС- прямоугольный;

S АВС = ½ ∙ АВ ∙ АС

В

А

С

5

6

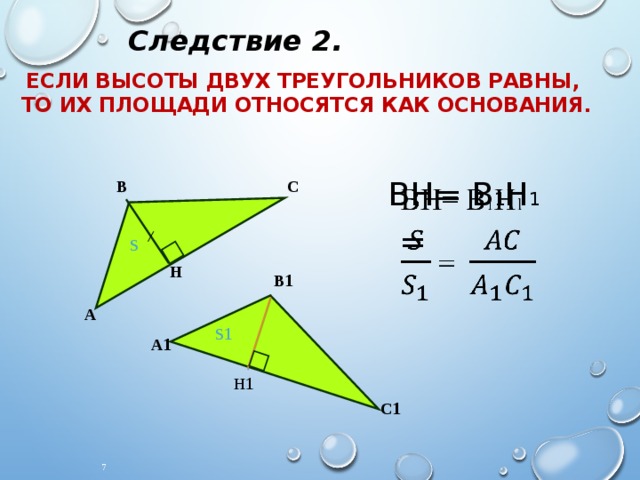
Следствие 2.

Если высоты двух треугольников равны, то их площади относятся как основания.

ВН= В 1 Н 1

=

С

В

S

Н

В 1

А

S 1

А 1

Н 1

С 1

6

7

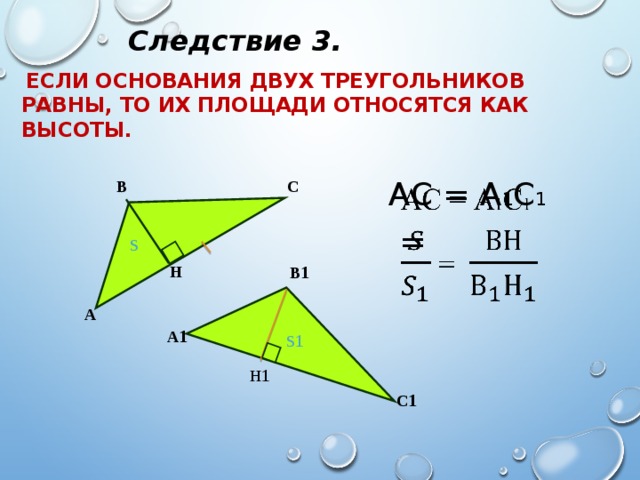
Следствие 3.

Если основания двух треугольников равны, то их площади относятся как высоты.

АС = А 1 С 1

=

В

С

S

В 1

Н

А

А 1

S 1

Н 1

С 1

А

В

С

S

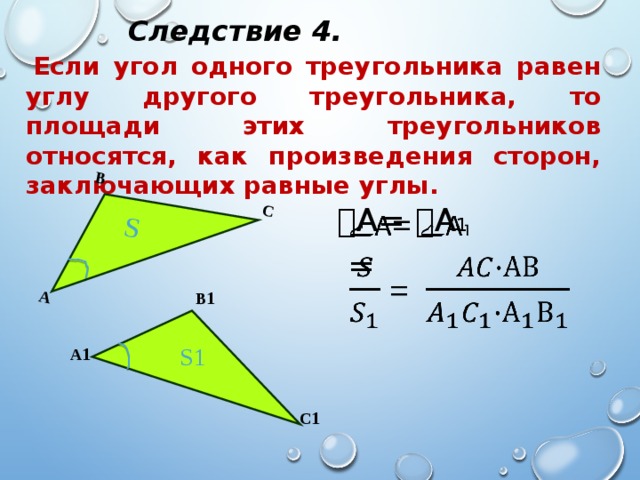
Следствие 4.

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся, как произведения сторон, заключающих равные углы.

ے А= ے А 1

=

В 1

S1

А 1

С 1

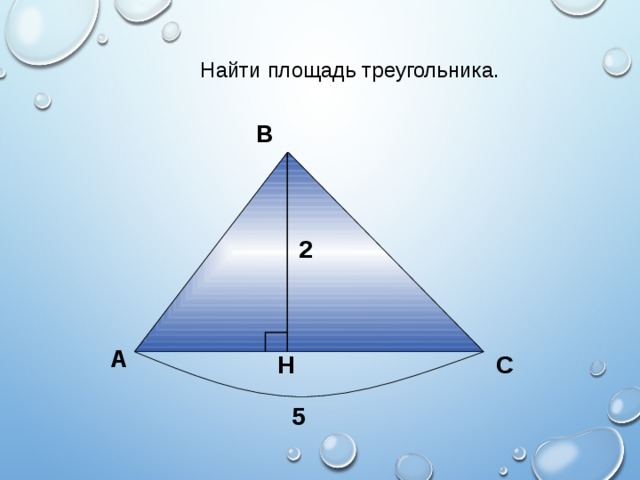
Найти площадь треугольника.

В

2

А

С

H

5

11

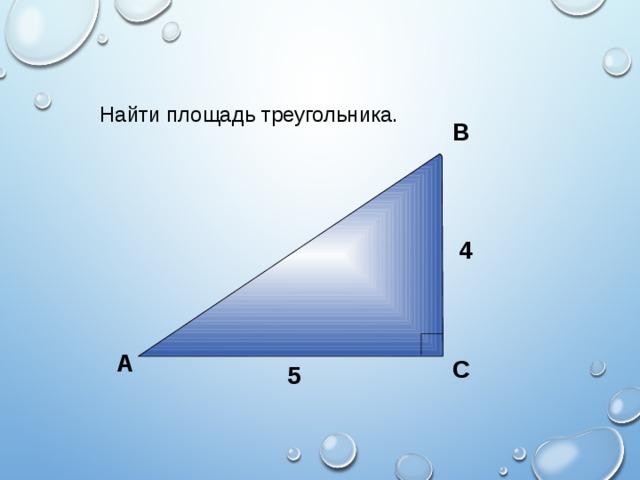
Найти площадь треугольника.

В

4

А

С

5

12

В

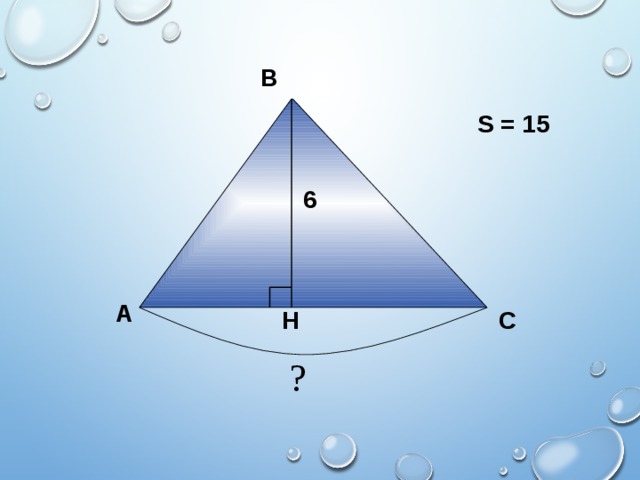
S = 15

6

А

С

H

?

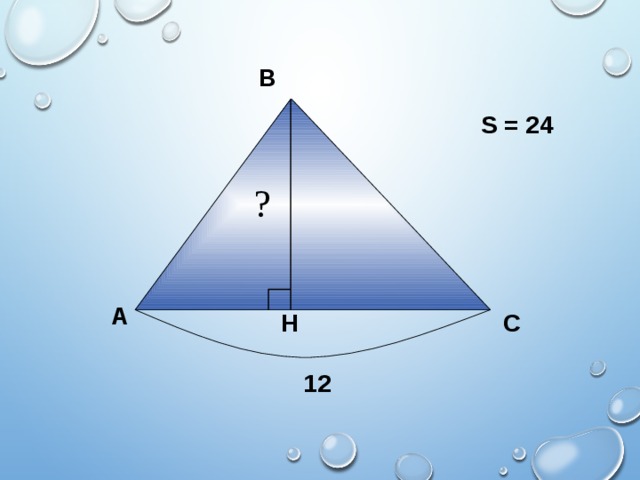
В

S = 24

?

А

С

H

12

№ 468 (а, б), 471 ,474