
Тема
Пирамида

Пирамида. Её элементы. Правильная пирамида.
Тема урока
- Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды , точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину с точками основания.

Слово «пирамида» — греческое.
По мнению одних исследователей,
большая куча пшеницы
и стала прообразом
пирамиды. По мнению
других учёных, это слово
произошло от названия
поминального пирога
пирамидальной формы.

- Пирамиды майя в Сальвадоре

- Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта.
- Всего в Египте было обнаружено 118 пирамид.

- Пирамиды считаются проводниками космических энергий. Хорошо известно их применение в целительстве и медитации. Фактически, большинство храмов, мечетей, церквей, соборов имеют пирамидо- или куполообразную форму крыши.

Современные пирамиды
- Самая большая пирамида, высотой 44 метра, расположена в Московской области .

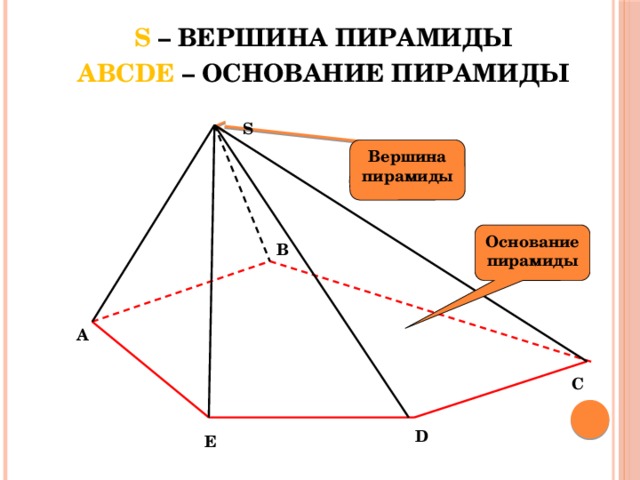
S – ВЕРШИНА ПИРАМИДЫ
ABCDE – ОСНОВАНИЕ ПИРАМИДЫ
S
Вершина пирамиды
Основание пирамиды
B
A
C
D
E
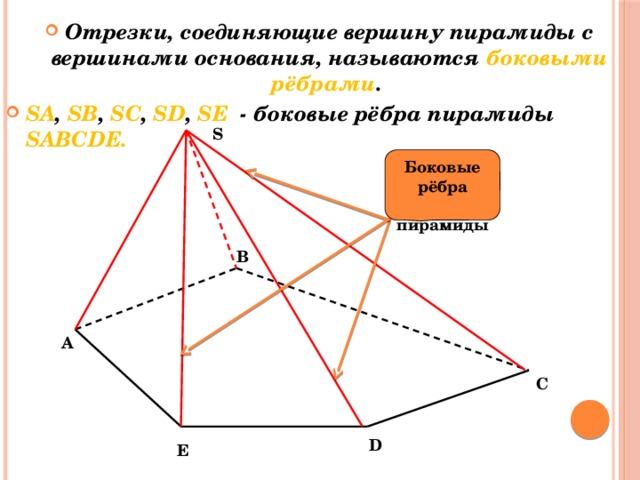
- Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми рёбрами .
- SA , SB , SC , SD , SE - боковые рёбра пирамиды SABCDЕ.
S
Боковые рёбра
пирамиды
B
A
C
D
E
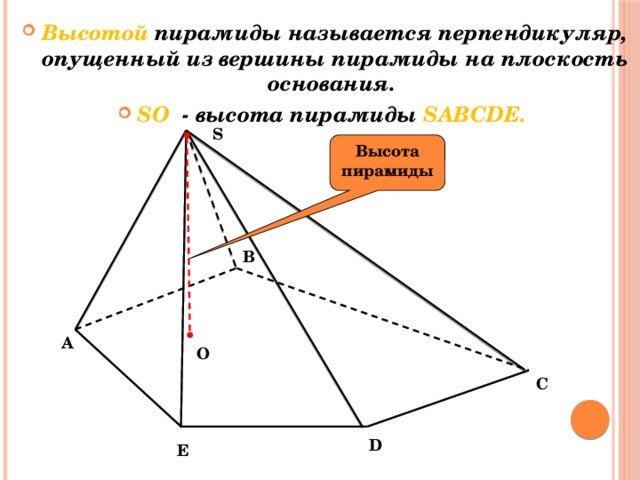
- Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
- SО - высота пирамиды SABCDЕ.
S
Высота пирамиды
B
A
О
C
D
E
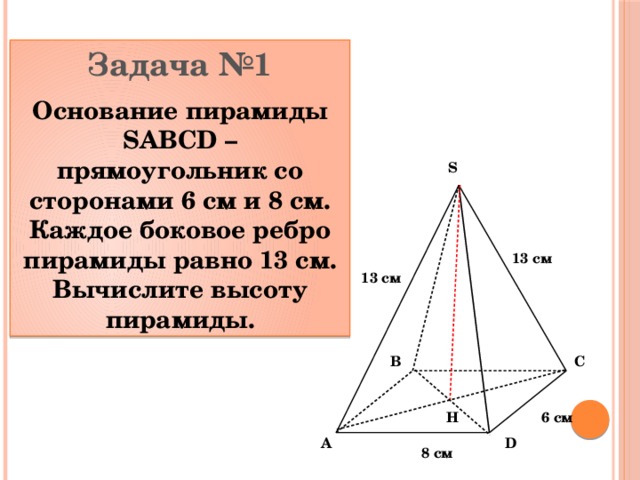
Задача №1
Основание пирамиды SABCD – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
S
13 см
13 см
C
B
6 см
Н
A
D
8 см
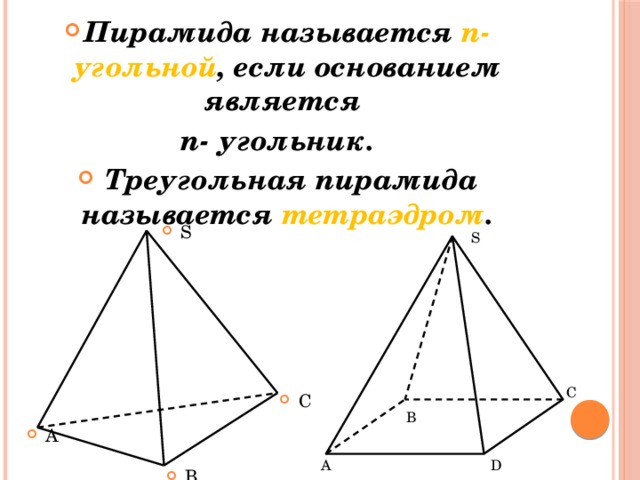
- Пирамида называется n- угольной , если основанием является
n- угольник.
- Треугольная пирамида называется тетраэдром .
S
C
B
A
D
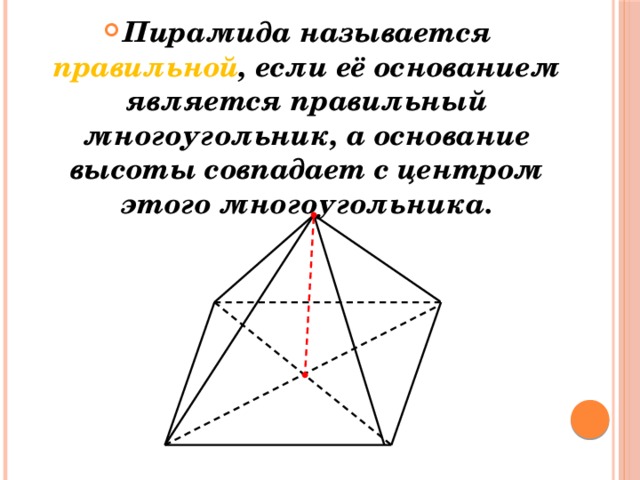
- Пирамида называется правильной , если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
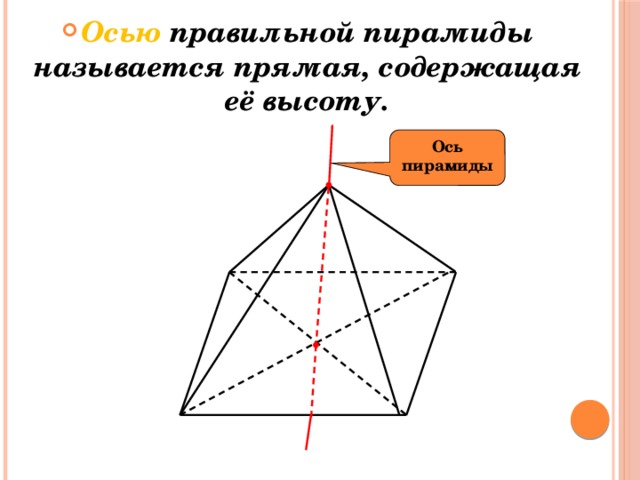
- Осью правильной пирамиды называется прямая, содержащая её высоту.
Ось пирамиды
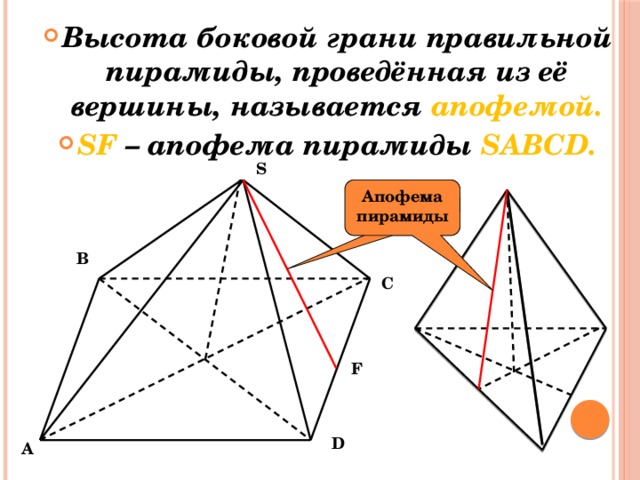
- Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
- SF – апофема пирамиды SABCD.
S
Апофема пирамиды
Апофема пирамиды
B
С
F
D
A
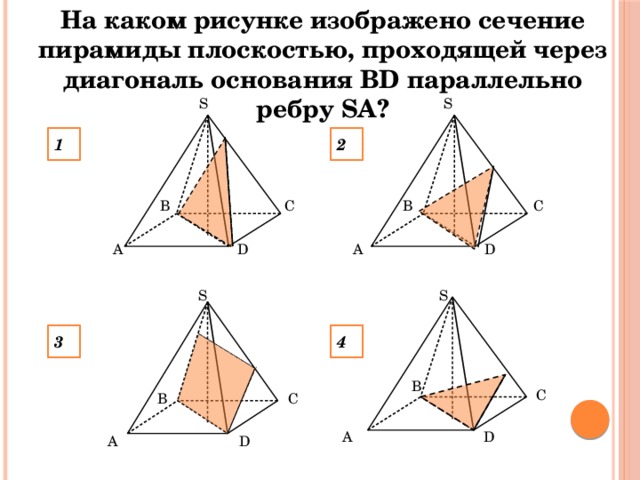
На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA?
S
S
1
2
B
C
C
B
D
A
A
D
S
S
3
4
B
C
B
C
A
D
D
A
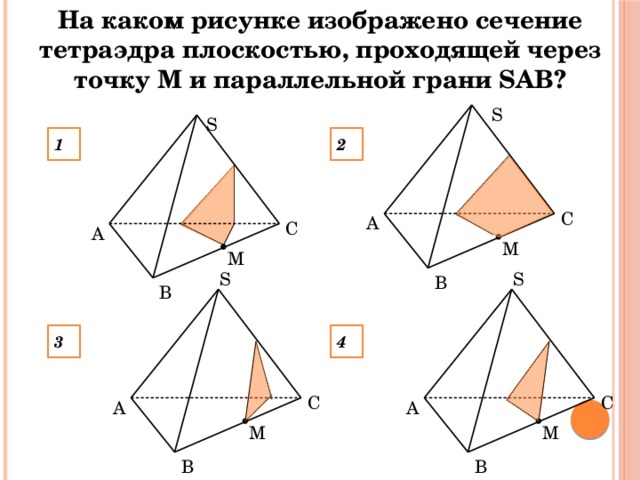
На каком рисунке изображено сечение тетраэдра плоскостью, проходящей через точку М и параллельной грани SAВ?
S
S
1
2
C
A
C
A
M
M
S
S
B
B
3
4
C
C
A
A
M
M
B
B
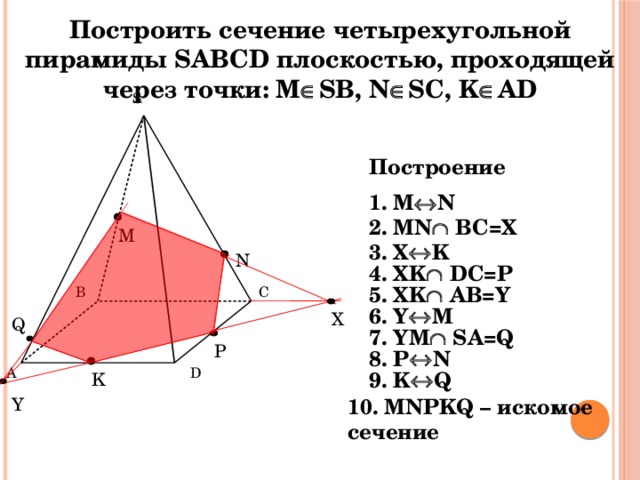
Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через точки: M SB, N SC, K AD
S
Построение
1. M N
2. MN BC=X
M
3. X K
N
4. XK DC=P
5. XK AB=Y
B
C
6. Y M
X
Q
7. YM SA=Q
P
8. P N
A
D
9. K Q
K
Y
10. MNPKQ – искомое сечение
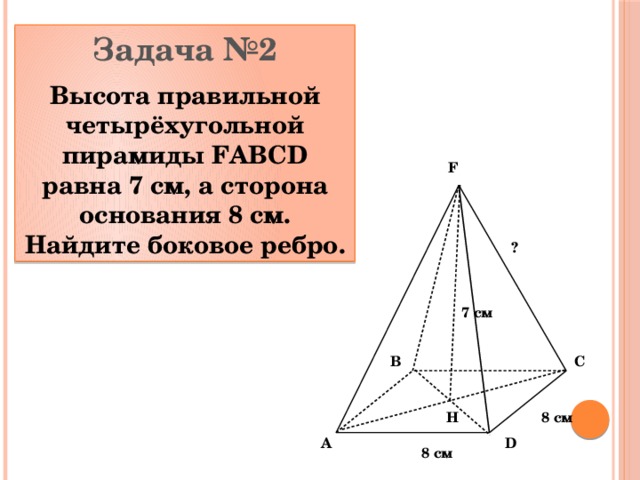
Задача №2
Высота правильной четырёхугольной пирамиды FABCD равна 7 см, а сторона основания 8 см. Найдите боковое ребро.
F
?
7 см
C
B
8 см
Н
D
A
8 см

Усечённая пирамида
Тема урока

- Рассмотрим пирамиду PA 1 A 2 …A n и проведём секущую плоскость ß, параллельную плоскость и α основания пирамиды и пересекающую боковые рёбра в точках В 1 , В 2 … В n .
- Плоскость ß разбивает пирамиду на 2 многогранника.
- A 1 A 2 …A n В 1 В 2 … В n – усечённая пирамида .
- A 1 В 1 ,…A n В n – боковые рёбра.
- A 1 В 1 В 2 A 2 … - боковые грани.
- A 1 A 2 …A n , В 1 В 2 … В n – основания усечённой пирамиды

Теорема
- Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду.
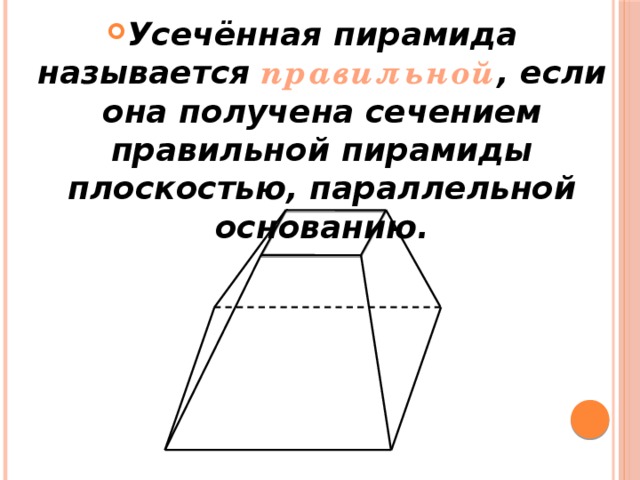
- Усечённая пирамида называется правильной , если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Площадь боковой поверхности пирамиды
Тема урока

- Боковой поверхностью пирамиды называется сумма площадей её боковых граней.
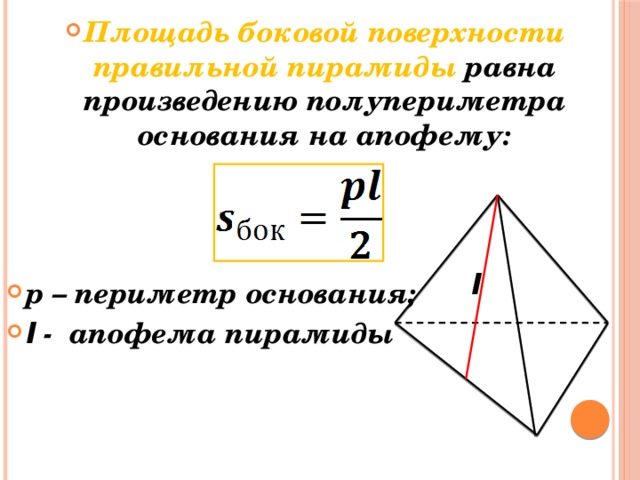
- Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему:
- p – периметр основания;
- l - апофема пирамиды
l

- Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему:
- p 1 и p 2 – периметры оснований;
- l - апофема пирамиды.
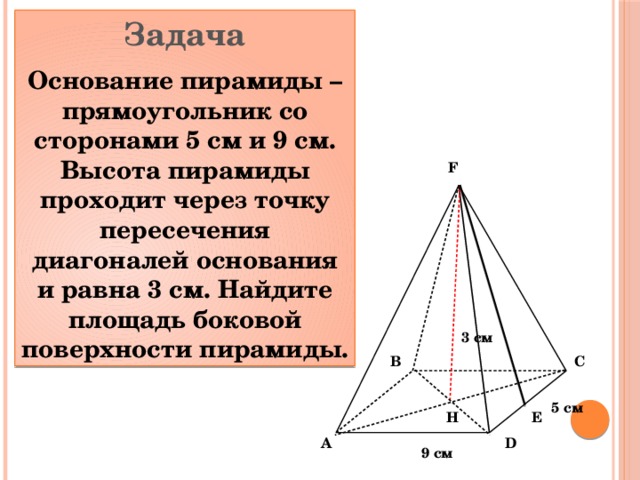
Задача
Основание пирамиды – прямоугольник со сторонами 5 см и 9 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 3 см. Найдите площадь боковой поверхности пирамиды.
F
3 см
C
B
5 см
Н
Е
D
A
9 см

Площадь полной поверхности пирамиды
Тема урока

- Площадь полной поверхности правильной пирамиды равна сумме площади боковой поверхности и площади основания:
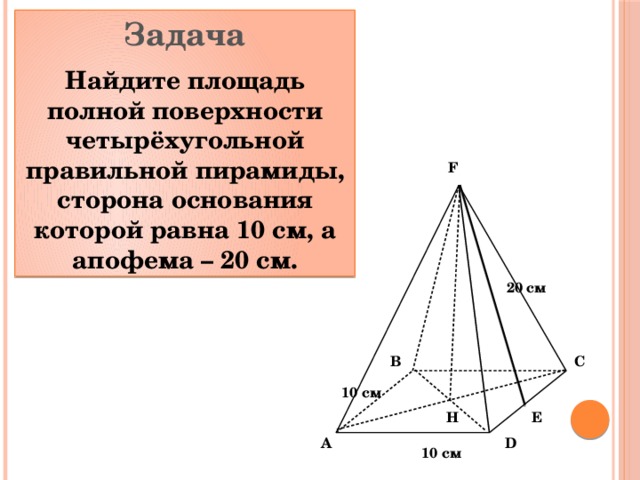
Задача
Найдите площадь полной поверхности четырёхугольной правильной пирамиды, сторона основания которой равна 10 см, а апофема – 20 см.
F
20 см
C
B
10 см
Н
Е
D
A
10 см

Объём пирамиды
Тема урока
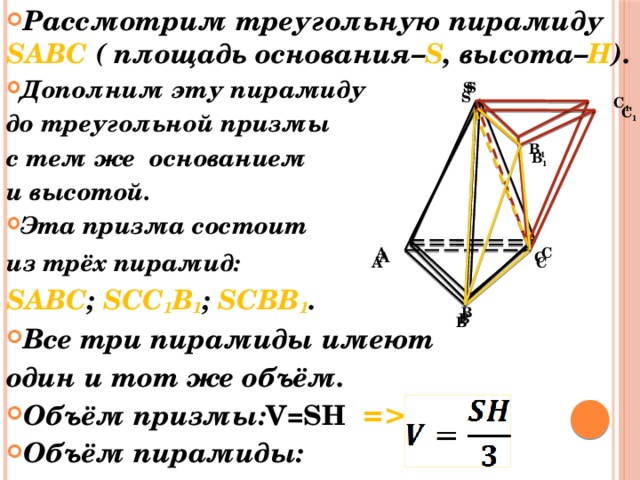 Объём пирамиды: S S S C 1 C 1 B 1 B 1 С A С A С A В В В " width="640"
Объём пирамиды: S S S C 1 C 1 B 1 B 1 С A С A С A В В В " width="640"
- Рассмотрим треугольную пирамиду SABC ( площадь основания– S , высота– H ).
- Дополним эту пирамиду
до треугольной призмы
с тем же основанием
и высотой.
из трёх пирамид:
SABC ; SCC 1 B 1 ; SCBB 1 .
один и тот же объём.
- Объём призмы: V=SH =
- Объём пирамиды:
S
S
S
C 1
C 1
B 1
B 1
С
A
С
A
С
A
В
В
В

- Объём любой пирамиды равен одной трети произведения площади её основания на высоту:

Объём усечённой пирамиды
Тема урока

- Объём усечённой пирамиды с площадями оснований Q 1 и Q 2 и высотой H :
Q 1
H
Q 2

Решение задач
Тема урока
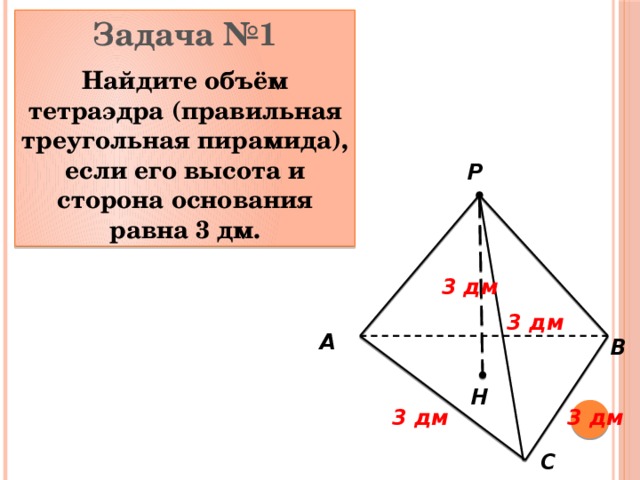
Задача №1
Найдите объём тетраэдра (правильная треугольная пирамида), если его высота и сторона основания равна 3 дм.
P
3 дм
3 дм
A
B
H
3 дм
3 дм
C
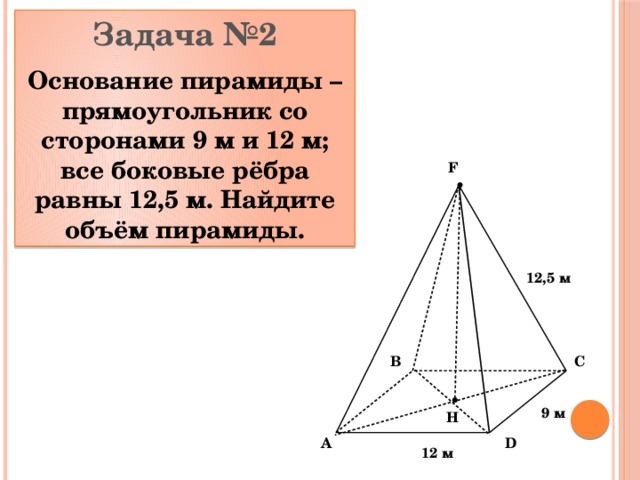
Задача №2
Основание пирамиды – прямоугольник со сторонами 9 м и 12 м; все боковые рёбра равны 12,5 м. Найдите объём пирамиды.
F
12,5 м
C
B
9 м
Н
D
A
12 м
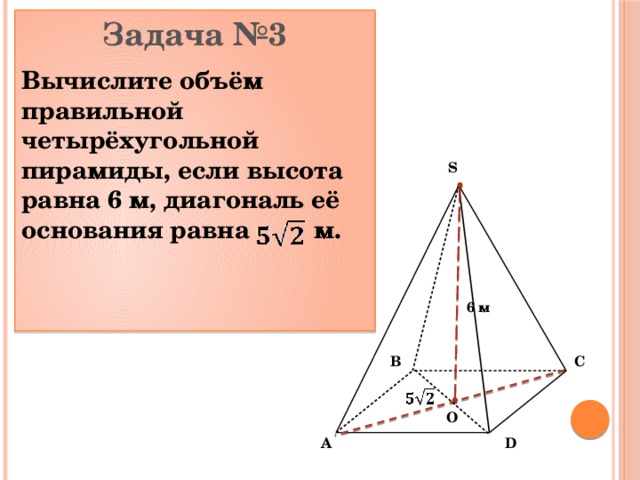
Задача №3
Вычислите объём правильной четырёхугольной пирамиды, если высота равна 6 м, диагональ её основания равна м.
S
6 м
C
B
O
D
A
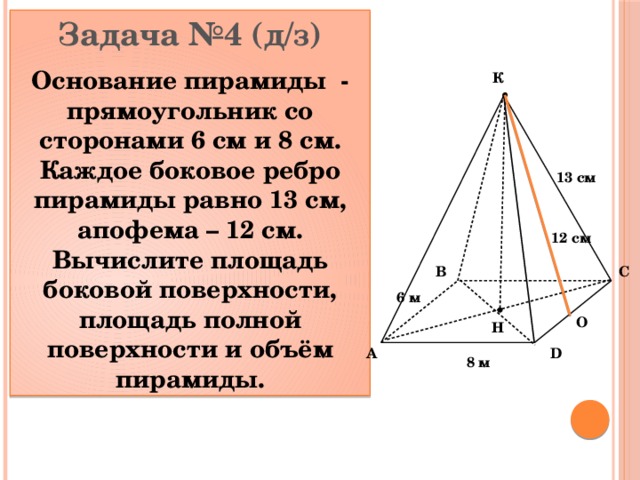
Задача №4 (д/з)
Основание пирамиды - прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см, апофема – 12 см. Вычислите площадь боковой поверхности, площадь полной поверхности и объём пирамиды.
К
13 см
12 см
C
B
6 м
О
Н
D
A
8 м

Зачёт по теме: «Пирамида»
Тема урока

План выполнения работы:
- Определить вид данной фигуры.
- Определить необходимые измерения для уточнения вида фигуры.
- Записать формулы вычисления периметра и площади основания данной фигуры.
- Записать формулу вычисления боковой поверхности данной фигуры.
- Записать формулу вычисления полной поверхности.
- Записать формулу для вычисления объёма данной фигуры.
- Произвести непосредственные измерения соответствующих элементов.
- Вычислить периметр основания данной фигуры.
- Вычислить площадь боковой поверхности фигуры.
- Вычислить площадь основания данной фигуры.
- Вычислить площадь полной поверхности фигуры.
- Вычислить объём тела.


 Получите свидетельство
Получите свидетельство Вход
Вход




































 Объём пирамиды: S S S C 1 C 1 B 1 B 1 С A С A С A В В В " width="640"
Объём пирамиды: S S S C 1 C 1 B 1 B 1 С A С A С A В В В " width="640"



















 Пирамида (7.58 MB)
Пирамида (7.58 MB)
 10
10 4687
4687 615
615


Очень понравилась презентация!
Смотрите внизу любого письма рассылки