Пирамида и правильные многогранники

МБОУ СОШ №5 – «Школа здоровья и развития»

Пирамида

Учитель математики Семёнова Е.Ю.

Содержание

• Примеры пирамид
• Определение пирамиды
• Виды пирамид
• Правильные пирамиды
• Построение правильной пирамиды
• Свойства правильной пирамиды
• Усеченная пирамида
• Площадь поверхности пирамиды

Пир ами ды древности

Пир ами ды древности

Пир ами ды древности

Магические пирамиды

Пирамиды

Примеры пирамид

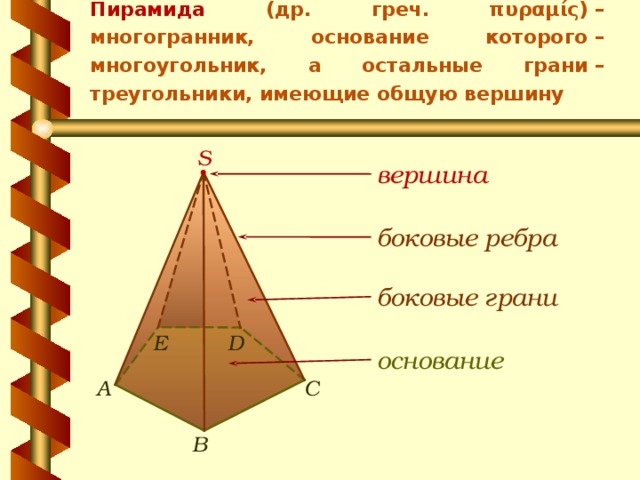
Пирамида (др. греч. πυραμίς) – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину

S

вершина

• вершина

боковые ребра

боковые грани

D

E

основание

C

А

B

Виды пирамид

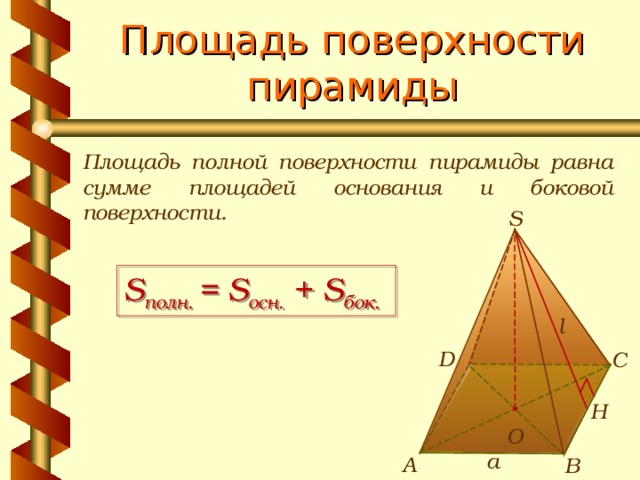
Площадь поверхности пирамиды

Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности.

S

S полн. = S осн. + S бок.

l

D

С

Н

О

а

А

В

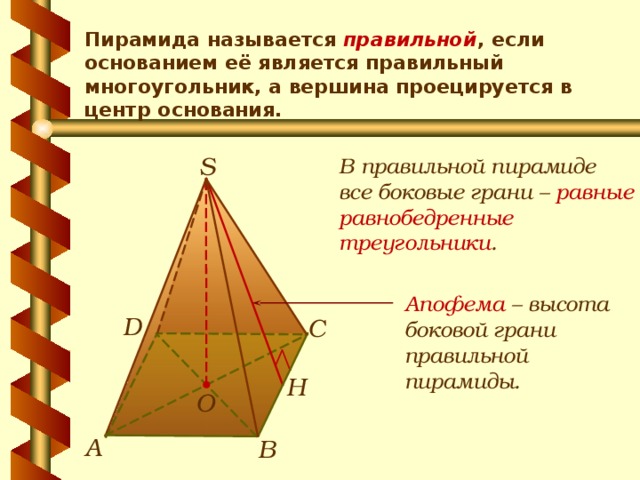
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

S

В правильной пирамиде все боковые грани – равные равнобедренные треугольники .

Апофема  – высота боковой грани правильной пирамиды.

D

С

Н

О

А

В

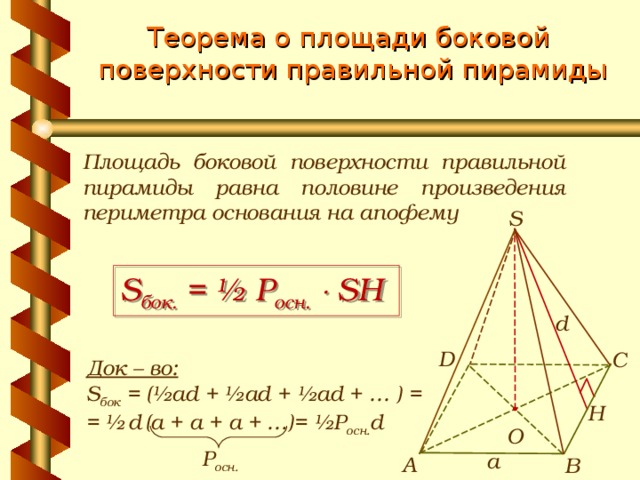
Теорема о площади боковой поверхности правильной пирамиды

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

S

S бок. = ½ P осн.  SH

d

D

С

Док – во:

S бок = (½ad + ½ad + ½ad + … ) =

= ½ d (a + a + a + …)= ½P осн . d

Н

О

P осн .

а

А

В

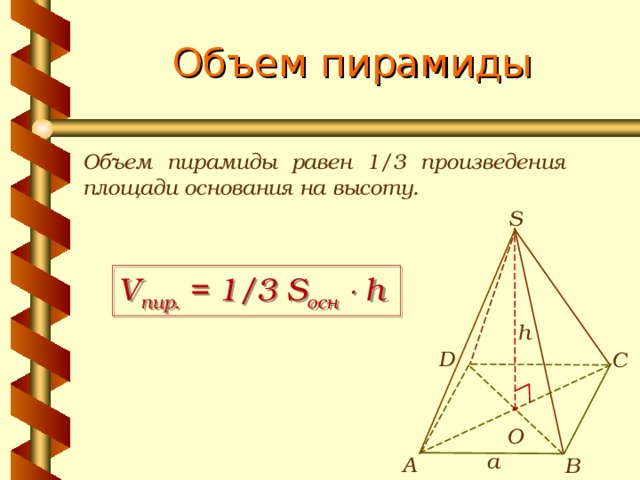
Объем пирамиды

Объем пирамиды равен 1/3 произведения площади основания на высоту.

S

V пир. = 1/3 S осн  h

h

D

С

О

а

А

В

Построение правильных пирамид

S

S

S

C

С

А

D

M

O

O

M

В

А

В

E

F

A

D

O

M

B

C

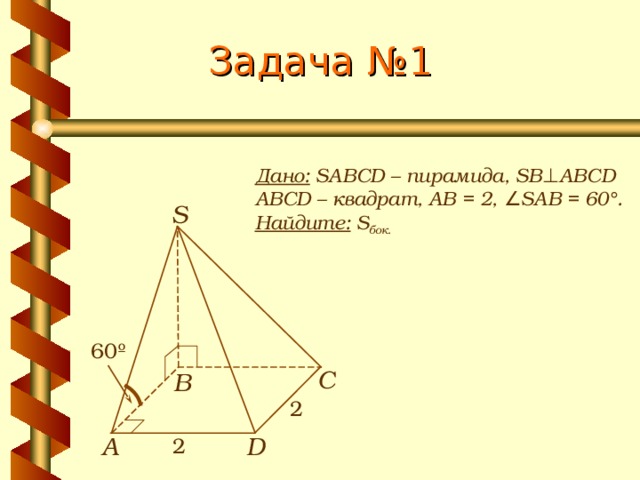
Задача №1

Дано: SABCD – пирамида, SB ⊥ ABCD

ABCD – квадрат, АВ = 2 , ∠SAB = 60°.

Найдите: S бок.

S

60º

С

В

2

А

D

2

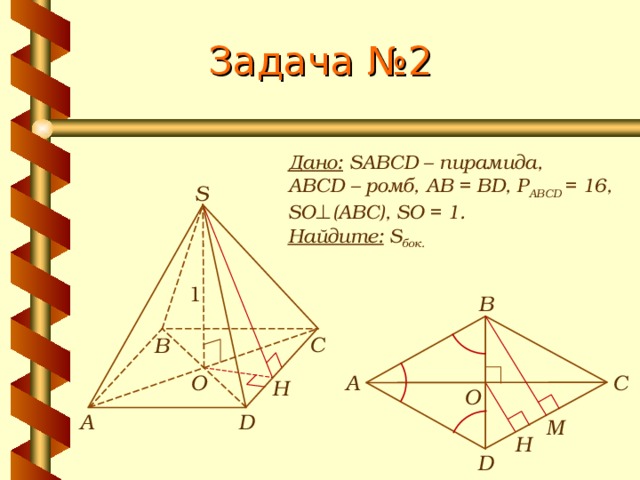
Задача № 2

Дано: SABCD – пирамида,

ABCD – ромб, АВ = BD, Р ABCD = 16,

SO ⊥ (АВС), SO = 1.

Найдите: S бок.

S

1

В

С

В

С

А

O

H

O

D

А

М

H

D

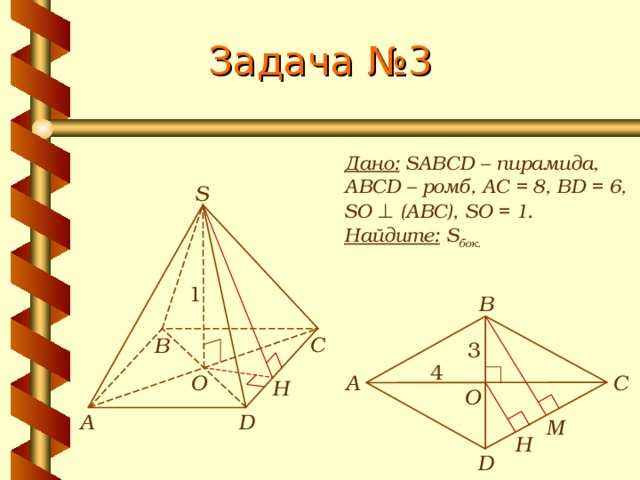
Задача № 3

Дано: SABCD – пирамида,

ABCD – ромб, АС = 8, BD = 6,

SO ⊥ (АВС), SO = 1.

Найдите: S бок.

S

1

В

С

В

3

4

С

А

O

H

O

D

А

М

H

D

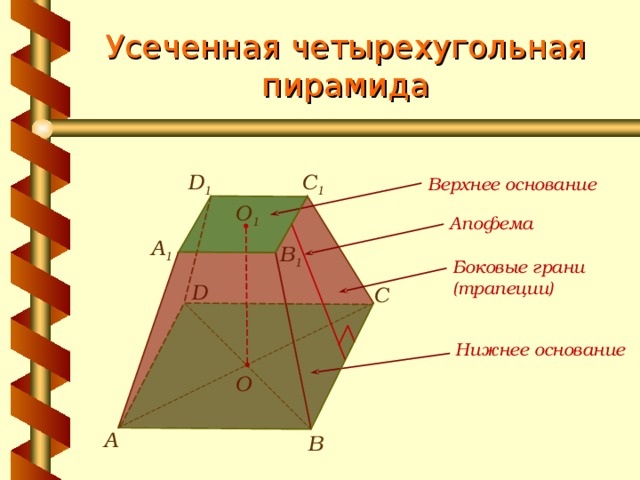
Усеченная четырехугольная пирамида

C 1

D 1

Верхнее основание  

О 1

Апофема  

A 1

B 1

Боковые грани

(трапеции)  

D

С

Нижнее основание

О

А

В

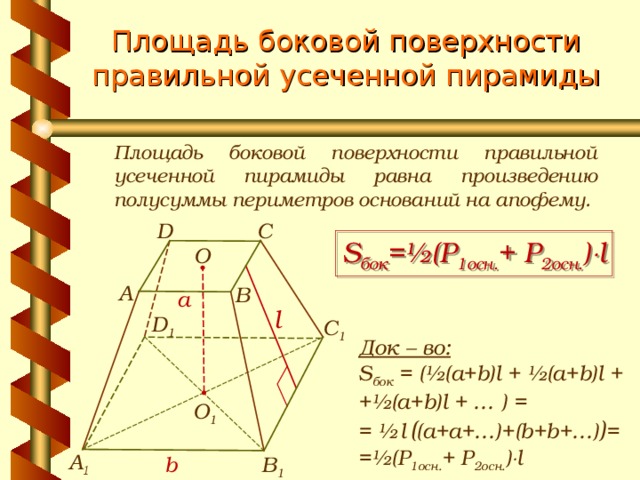
Площадь боковой поверхности правильной усеченной пирамиды

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

C

D

S бок =½ ( P 1осн. + P 2 осн. )  l

О

A

B

a

l

D 1

С 1

Док – во:

S бок = (½(a+b)l + ½(a+b)l + +½(a+b)l + … ) =

= ½ l ( (a+a+…)+(b+b+…) ) =

=½ ( P 1осн. + P 2 осн. )  l

О 1

А 1

В 1

b

Усеченная треугольная пирамида

C 1

A 1

О 1

Н 1

В 1

С

А

F

О

E

Н

В