Перпендикулярность прямой и плоскости

Перпендикулярность прямой и плоскости

Определение 1:

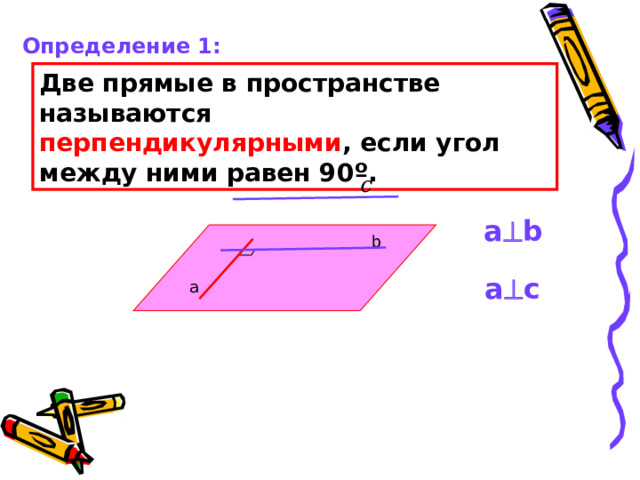
Две прямые в пространстве называются

перпендикулярными , если угол

между ними равен 90º.

c

a  b

b

a  c

a

Лемма:

Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна третьей прямой.

а

b

c

b || МА 3. b || МА с || МС МА  МС = b  с а b Лемма доказана c А М С α " width="640"

Доказательство:

1. Через точку М проведем прямые МА и МС:

МА||а, МС||с

Т.к. а  с, то  АМС=90°

2. По условию: b||а

по построению: МА||а

= b || МА

3. b || МА

с || МС

МА  МС

= b  с

а

b

Лемма доказана

c

А

М

С

α

Определение 2:

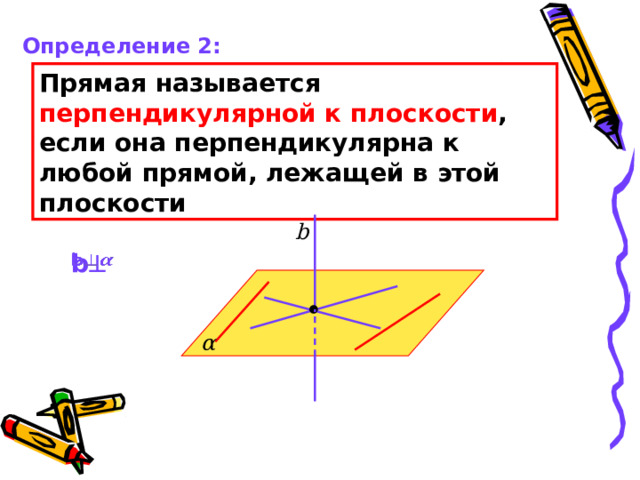
Прямая называется перпендикулярной к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости

b

b 

α

Теорема 1:

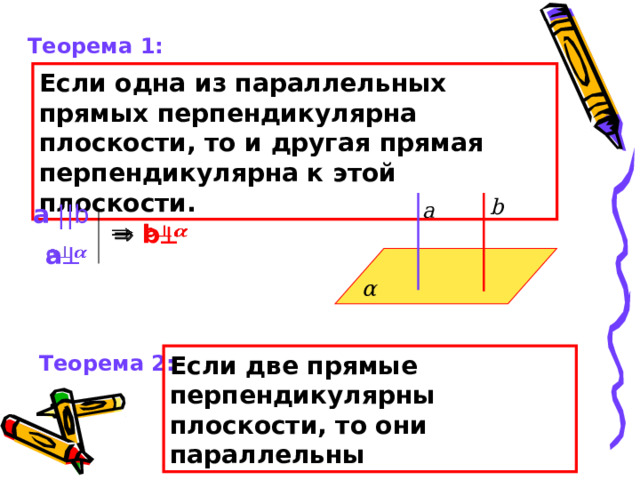
Если одна из параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.

b

а

а || b

 b 

а 

α

Теорема 2:

Если две прямые перпендикулярны плоскости, то они параллельны

Теорема 3:

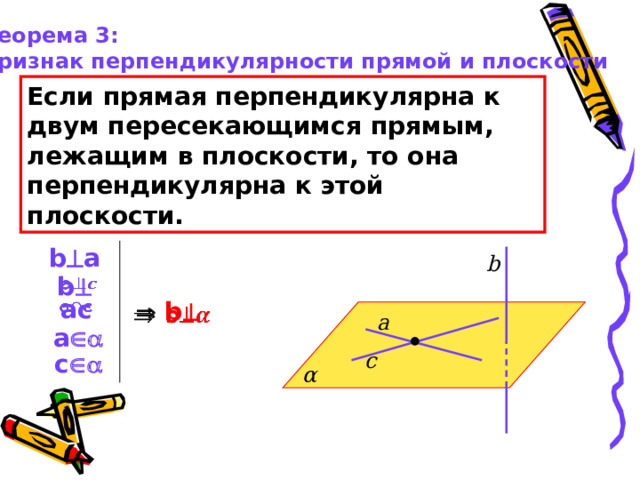
признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

b  a

b

b 

а c

 b 

а

а 

с

c 

α

Теорема 4:

о прямой, перпендикулярной к плоскости

Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и при том только одна.

Дано: М, 

М

Доказать:

α

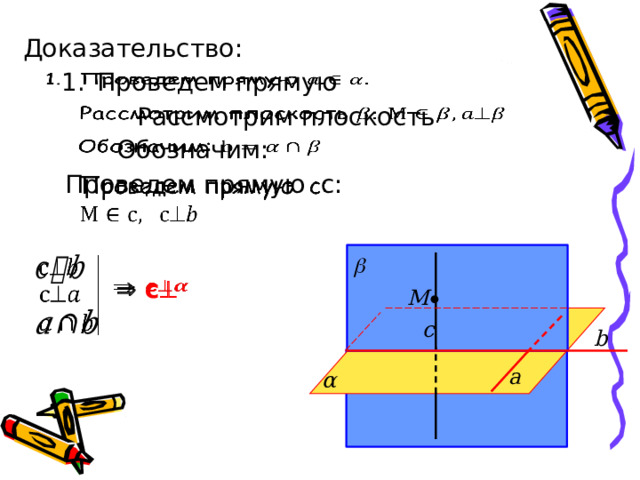
Доказательство:

• Проведем прямую

Рассмотрим плоскость

Обозначим:

Проведем прямую c:



 c 

М

с

b

а

α

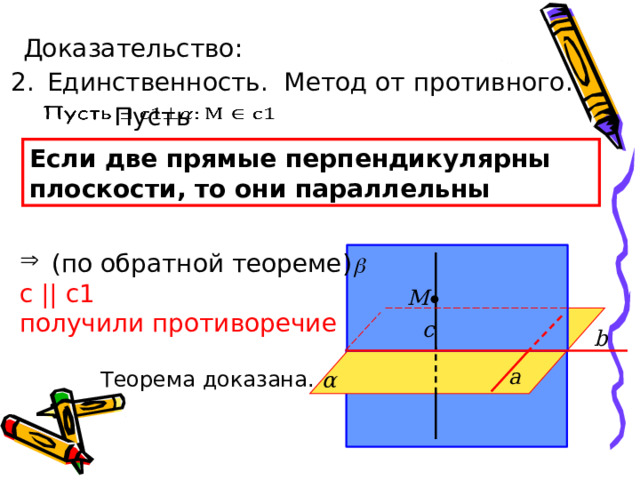
Доказательство:

• Единственность. Метод от противного.

Пусть

Если две прямые перпендикулярны плоскости, то они параллельны

• (по обратной теореме)

с || с1

получили противоречие



М

с

b

а

Теорема доказана.

α