МАТЕМАТИЧЕСКИЙ ДИКТАНТ
1. Прямые AM и CE пересекаются в точке О. Отметьте дугами вертикальные углы и выпишите их обозначения.
2. Чему равен угол, если вертикальный с ним угол равен 34°.
3. Один из четырех углов, получившихся при пересечении двух прямых, равен 140°. Чему равны остальные углы (только ответы).
4. Два угла с общей вершиной равны. Обязательно ли они вертикальные?
5. Первый угол равен 40°, второй - 140°. Могут ли эти углы быть смежными?

Решите устно: Один из углов, образовавшихся при пересечении двух прямых – прямой. Найти остальные углы.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Теорема.
Две прямые, перпендикулярные к третьей, не пересекаются.
Доказательство - смотри презентацию.

 Получите свидетельство
Получите свидетельство Вход
Вход























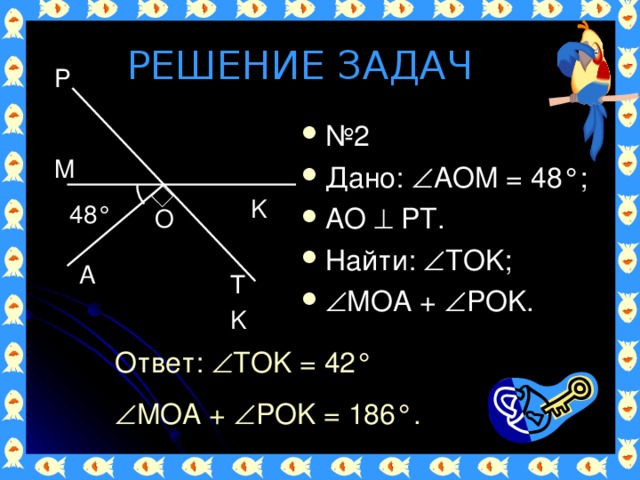










 Перпендикулярные прямые (1.09 MB)
Перпендикулярные прямые (1.09 MB)
 0
0 1141
1141 206
206 Нравится
0
Нравится
0




