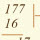Перевод чисел в различные системы счисления

Тип урока: урок обобщения и систематизации знаний учащихся.

Цели урока:

1. Закрепление, обобщение знаний по теме «Системы счисления»;
2. Сформировать у учащихся навыки и умения перевода из любой системы счисления в любую;

Задачи урока:

ü  совершенствовать навыки перевода чисел из одной системы счисления в другую;

ü  развивать познавательные процессы (внимание, память, восприятие);

ü  воспитание активности учащихся; привитие навыков самостоятельной работы; обеспечение сознательного усвоения материала.

Требования к знаниям и умениям:

Учащиеся должны знать: развернутую форму записи числа.

Учащиеся должные уметь: переводить числа из одной системы в десятичную

Оборудование и программное обеспечение: ПК, проектор, программа Калькулятор.

Формы и методы: словесная, фронтальная, объяснительно-иллюстративный, практическая, самостоятельная работа, работа на компьютере

Ожидаемый результат: закрепление навыков по переводе из одной системы счисления в другую

План  урока:

I.Организационный момент.

 (Приветствие, объявление целей урока слайд 1и 2)

II. Постановка целей урока.

Ребята, мы научились переводить числа из разных систем счислений в другие и сегодня нам нужно закрепить и систематизировать знания по теме. Давайте  вместе вспомним:  какие знания и умения приобрели мы  на  прошлых  уроках?

III. Актуализация знаний.

Тест из 8 вопросов.

1. Система счисления это –

1.      Представление чисел в экспоненциальной форме

2.      Представление чисел с постоянным положением запятой.

3.      Способ представления чисел с помощью символов, имеющих определенное количественное значение.

2. В какой системе счисления может быть записано число 402?

1.      В двоичной

2.      В троичной

3.      В пятеричной

3. В зависимости от способа изображения чисел системы счисления делятся на:

1. Арабские и римские
2. Позиционные и непозиционные
3. Представление в виде ряда и в виде разрядной сетки
4. Пятеричная система счисления имеет основание:

1. 5
2. 3
3. 4

5. Цифры – это:

1. Символы, участвующие в записи числа.
2. Буквы, участвующие в записи числа;
3. Пиктограммы, участвующие в записи числа.

6. Когда 2*2=11

1. В двоичной системе счисления
2. В троичной системе счисления
3. В четверичной системе счисления

7. Какие цифры используется в семеричной системе счисления:

1. 0,1,6
2. 0,8,9
3. 1,6,7

IV.                 Повторение изученного материала

Давайте вспомним правила перехода  из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную  системы счисления.

( Для перевода необходимо: разделить на основание новой системы последовательно, выделяя остатки от деления. Результат записывается справа налево)

177₁₀=10110001₂

(Пример на экране: слайд 11)

Задание № 1: (Выполняются у доски и в тетрадях)

    (слайд 12)

Задание № 2:  (Выполняются у доски и в тетрадях)

 ( слайд 13 )

324₁₀= 504₈

Давайте вспомним правило перехода из любой системы счисления в десятичную.

(Для перехода необходимо расписать число по степеням основания системы справа налево, начиная с нулевой степени. Цифры в числе являются коэффициентом при соответствующих степенях.)

(Пример на экране: слайд 14)

101101₂=1*2⁵+0*2⁴+1*2³+1*2²+0*2¹+1*2⁰=32+0+8+4+0+1=44₁₀

Задание № 3: (Выполняются у доски и в тетрадях)

Двоичное   число 11011101₂ перевести в десятичную систему.

(Для проверки показывается слайд 16  с ответами)

11011101₂=1*2⁷+1*2⁶+0*2⁵+1*2⁴+1*2³+1*2²+0*2¹+1*2⁰=128+64+0+16+8+4+0+1=221₁₀                                               

Задание №4: (Выполняются в тетрадях)

306₈=198₁₀  слайд 17

Задание № 5: (Выполняются в тетрадях)

B5₁₆=181₁₀                             слайд 18

Вспомните правило  перехода из двоичной системы счисления в восьмеричную.

(Число в двоичной системе разбить на триады справа налево и вместо триад по таблице написать восьмеричные.)

(Пример на экране: слайд 20)

  1.110.101.100₂=1654₈

Задание № 6: (Выполняются в тетрадях)

11.001.100.110₂=3146₈                            слайд 21

Вспомните правило  перехода из восьмеричной системы счисления в двоичную.

(Каждую восьмеричную цифру заменить двоичным классом по три цифры в каждом)

(Пример на экране: слайд 22)

2571₈=10.101.111.001₂

Задание № 7: (Выполняются в тетрадях)                    

702₈ =111.000.010₂                                     слайд 23

Вспомните правило  перехода из двоичной системы счисления в шестнадцатеричную.

(Разбить двоичное число на классы справа налево по четыре цифры в каждом. Заменить каждый класс соответствующей шестнадцатеричной цифрой.)

(Пример на экране: слайд 24)

1.1011.1000.1101₂=1B8D₁₆

Задание № 8: (Выполняются в тетрадях)

11001100111₂=667₁₆                               слайд 25

Вспомните правило  перехода из шестнадцатеричной системы счисления в двоичную.

(Каждую шестнадцатеричную цифру заменить двоичным классом по четыре цифры в каждом)

(Пример на экране: слайд 26)

 F54D0₁₆=1111.0101.0100.1101.0000₂

Задание № 9: (Выполняются в тетрадях)

B096₁₆=1011.0000.1001.0110₂,                  слайд 27

   V.  Закрепление

Задание №10 (слайд 28)

Переведите координаты точек в десятичную систему счисления. Отметьте точки на координатной плоскости и определите получившийся рисунок

Задание № 11 (слайд29)

Перед вами таблица, состоящая из 7 строк и 19 столбцов. В первом столбце записаны числа в разных системах счисления. Осуществите перевод этих чисел в двоичную систему счисления. Напротив каждого числа в нужной строке таблицы закрасьте те клетки, которые соответствуют единицам в получившемся двоичном числе. В итоге внутри вашей таблицы получится аббревиатура из букв – ключевое слово. Запишите это слово.

VI.             Домашнее задание (слайд 30)

Задача№1.

Существует ли такая система счисления, в которой 3+4=7, 3*4=13 и 39+29=70

Задача№2.

Переведите числа, записанные в различных системах счисления, в десятичную систему счисления; затем полученные после вычисления числа замените буквами русского алфавита, которые имеют  соответствующие порядковые номера; запишите полученное слово. (Ответ: ДИСКОВОД)