Открытый урок по теме «Прогрессии в окружающей нас жизни»

Открытый урок по теме «Прогрессии в окружающей нас жизни».

Тип урока: комбинированный.

Цели урока:

1) образовательные:

- продолжить работу над определениями арифметической, геометрической прогрессий; характеристическими свойствами, которым обладают члены прогрессий; выработать общие рекомендации по выполнению заданий, содержащих данные прогрессии;

- Выяснить, какое место в нашей жизни имеют арифметическая и геометрическая прогрессии, уловить взаимосвязь прогрессий и кредитования.

- убедится, что раздел математики «Прогрессии» являются неотъемлемой частью общечеловеческой культуры;
- продолжать формировать навыки применения прогрессии к решению прикладных задач;

-  обобщить и систематизировать знания учащихся по данной теме.

2) воспитательные:

- содействовать воспитанию интереса к математике и ее приложениям, активности, умению общаться, аргументировано отстаивать свои взгляды.

3) развивающие:

- продолжить дальнейшую работу по выработке умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности;

- учиться проводить рассуждения по аналогии; формировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.

Ход урока:

1. Организационный момент:

Здравствуйте, ребята! Отгадайте загадку:

Оно длиннее всего на свете — и короче.
Быстрее всего — и медленнее.
Самое дробное — и самое неразрывное.
Его меньше всего ценят, но больше всего сожалеют о его отсутствии.
Без него ничего не может быть сделано. 

Конечно же это время. И это понятие относительное. А у нас с вами времени 45 минут. Давайте научимся его ценить. Итак, начнем урок!!!

- Скоро вам предстоит сдавать выпускные экзамены, а чтобы успешно их сдать, нужно регулярно готовиться. Психологи рекомендуют начать подготовку с занятий 15 мин в день, увеличивая каждую неделю время занятий на 5 мин в день, но не превышая время 1час 35 мин.

Сколько времени следует уделить подготовке к экзамену на 5-й неделе? И на какой неделе ученик достигнет максимального времени подготовки?

У вас есть идеи?

- ученики предлагают идеи (фиксирую их на доске)

Например, узнаем сначала на второй неделе, затем на третьей…

-Что получили? (последовательность)

15, 20, 25, 30, 35…95мин

-На 5й неделе время 35 мин.

- И на какой неделе ученик достигнет максимального времени подготовки?

(17 неделе)

Как вы думаете, о чем идет речь?

-Давайте определим тему сегодняшнего урока.

-Какая же тема нашего сегодняшнего урока.

Итак, тема нашего урока «Прогрессии в окружающей нас жизни».

-Откройте свои тетради, запишите число, классная работа и тему нашего урока. Как вы думаете, чем мы будем заниматься на нашем уроке сегодня?

2. Актуализация знаний:

- Сегодня у нас заключительный урок по прогрессиям. Мы с вами изучили много формул, написали контрольную работу. А самое интересное я специально оставила для этого урока.

Часто вы задаете вопрос, где в дальнейшем вы сможете применить полученные знания. На этом уроке мы узнаем в каких областях знаний используется арифметическая и геометрическая прогрессии.

Почти весь месяц мы всем классом готовили исследовательский проект по теме «Прогрессии». Основанием для этой работы послужили два момента: противоречия, возникшие между нами. Одни считали, что прогрессии абсолютно не пригодятся в жизни, другие же были уверены в обратном. Второй момент заключается в том, некоторые задачи, связанные с прогрессиями, вызвали у многих неподдельный интерес.

Мы назвали наш проект «Прогрессии в окружающей нас жизни».

-Что обозначает слово «прогрессия»?

Ответ: движение вперед.

-Сегодня мы будем двигаться вперед и еще раз убедимся, и убедим всех присутствующих гостей в том, что…

- что раздел математики «Прогрессии» является неотъемлемой частью общечеловеческой культуры;

- прогрессия – это не просто математическая «игрушка», а мощный инструмент для решения реальных задач в различных сферах человеческой жизни;

- что знания по прогрессиям необходимы в банковских расчетах, в микробиологии и медицине, в строительстве и даже спорте.

- что задания по прогрессиям встречаются в олимпиадных задачах.

Проблемный вопрос: Зачем нужно изучать прогрессии? Действительно ли прогрессии играют большую роль в повседневной жизни? 

Над проектом у нас работали три группы. (историки, микробиологи и медики, экономисты и математики). Каждая группа готовила теоретический материал и задачи в своем направлении. Слово предоставляется группе историков. Они скажут несколько слов о появлении прогрессий и предложат нашему вниманию интересные исторические задачи на прогрессии.

1. История. Ученик: Термин «прогрессия» имеет латинское происхождение и был введен римским автором Боэцием в 6 веке. Первые представления об арифметической и геометрической прогрессиях были еще у древних народов. Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.

В развитие теории о прогрессиях внесли свой вклад такие ученые, как Архимед, Пифагор и его ученики, французские математики Леонард Фибоначчи , немецкие математики М. Штифель, К. Гаусс.

Мы предложим вам очень интересные исторические задачи.

Рассмотрим задачу из старинного учебника арифметики Магницкого.

Задача №1 (из учебника Магнитского):

Богач-миллионер возвратился из отлучки необычайно радостный: у него была по дороге счастливая встреча, сулившая большие выгоды.

Рассказывает он домашним: «Вот и на мою деньгу денежка бежит. Повстречался мне в пути незнакомец, из себя не видный. Предложил выгодное дельце, что у меня дух захватывает».

«Сделаем,- говорит, - такой уговор. Я буду целый месяц приносить тебе ежедневно по сотне тысяч рублей. Недаром, разумеется, но плата пустяшная. В первый день я должен по уговору заплатить – всего 1 копейку. А за вторую сотню тысяч – 2 копейки. И так целый месяц, каждый день вдвое больше предыдущего. Находим выгодность сделки.

Решение: Деньги, отданные богачом незнакомцу, составляют геометрическую прогрессию, например, (b ).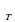

Сумма, отданная богачом незнакомцу в последний день

b₁ = 0,01; q = 2

b₃₀ = b₁  q²⁹ = 0,01  2 ²⁹ = 5 368 709, 12 =5 368 709 рублей 12 копеек

Сумма, полученная незнакомцем от миллионера за 30 дней

S = 2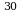 – 1 =10737418,23копеек 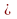11 миллионов рублей.

Незнакомец заплатил богачу: 30∙100 тыс = 3000 тыс. = 3000000 рублей.

Убыток 11000000 – 3000000=8000000 рублей.

Спасибо историкам. Пришла очередь экономистам показать, чем они занимались в рамках нашего проекта.

1. Экономика. Самые два распространенные вопроса в современной жизни это если взять кредит, сколько денег придется вернуть через несколько лет и, конечно если держать деньги в банке сколько я получу через какое-то время.

Прогрессия имеет очень широкое применение в экономике. Изучая материалы, связанные с прогрессиями, мы нашли большое количество задач с экономическим содержанием. Это задачи на банковские проценты на вклад, изменение оплаты труда и увеличение производства на предприятии, изменение цены товара и т. д.

Давайте решим задачу (Задания из сборника, предназначенного для подготовки к ОГЭ по алгебре в 9 классе.)

Задача №2: Предприниматель взял в банке кредит 500000 рублей под 20% годовых ( к сумме вклада , лежащей на счету в начале года, добавляется 20% от этой суммы в конце года). Какую сумму должен он вернуть через 3 года?

Решение. Давайте обозначим 500 000 через а т.е. а= 500000, тогда

-в конце первого года он должен будет отдать, а+0,2а=1,2а

-в конце второго года 1,2а+0,2∙1,2а=1,2а(1+0,2)=1,2²∙а =1,44а

-в конце третьего года он должен будет вернуть

1,44а+0,2∙1,44а=1,44а(1+0,2)= 1,2³∙а=1,728∙500000=864000 рублей

Вопрос: Какая получается прогрессия?

Ответ: геометрическая

Вывод: значит если вы решите когда-нибудь взять кредит, то вспомните что вам отдать надо будет сумму, которая вырастет в геометрической прогрессии.

Спасибо экономистам за хорошую задачу. Пришла очередь третей группы, группы микробиологов и медиков.

3. Микробиологи и медики

Ученик: - Самым показательным примером прогрессий может служить природа. Ученые-биологи обнаружили, что одноклеточные микроорганизмы размножаются с геометрической прогрессией.

- Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. (геометрическая прогрессия). Результат каждого удвоения называется поколением. Рассмотрим следующую задачу.

Задача 3 Каждое простейшее одноклеточное животное инфузория–туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 1920?

Решение:

b₁ - первоначальное количество инфузорий;

b₂ - Количество инфузорий после первого деления;

b₃ - количество инфузорий после второго деления;

...

b₇ = 1920 - количество инфузорий после шестого деления.

Количество инфузорий постоянно увеличивается в 2 раза, значит мы имеем дело с геометрической прогрессией со знаменателем q = 2.

Запишем формулу n-ого члена геометрической прогрессии и подставим в нее всё, что нам известно.

b_n = b₁q^n-1     (n = 7);

1920 = b₁ · 2^7-1

b₁ = 1920 : 64 = 30.

Ответ: 30.

-А так же прогрессии применяются и в медицине. 

Ученик: Гомеопатия — терапевтический метод лечения, разработанный великим немецким врачом и ученым Самуилом Ганеманом (1755-1843). В основе гомеопатии лежит принцип подобия — вещество, способное в больших дозах вызывать определённые симптомы в организме, в малых дозах способно похожие симптомы лечить, т.е. подобное лечится подобным.

Задача №4: Больной принимает гомеопатическое лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Решение: (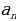 )- арифметическая прогрессия

На первом этапе приёма капель число принимаемых капель в день представляет собой возрастающую арифметическую прогрессию с первым членом, равным 5, разностью, равной 5 и последним членом, равным 40.

На втором этапе приёма капель число принимаемых капель в день представляет собой убывающую арифметическую прогрессию с первым членом, равным 40, разностью, равной 5 и последним членом, равным 5.

 = 5, d=5  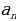, : 5, 10, 15,…,40, 40, 40, 35, 30,…,5
Найти : n-?, если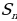 =180
Решение : а_n = а₁+d(n-1)  
40=5+5(n-1),     

n=8 

S_n=  n    
S₈ = (5+40)·8:2=180 ; 

180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400 (капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.

Ответ: 2 пузырька.

 Бытовая задачка. С ней может столкнуться в жизни любой человек. Зачем покупать лишнее дорогостоящее лекарство, когда достаточно всё просчитать.

5. В математике

И наконец, мы подошли к вопросу о том, где можно применить арифметическую и геометрическую прогрессию в математике. Вы можете встретить данные вопросы в олимпиаде или при поступлении в высшие учебные заведения, также вы должны видеть применение данной темы в других темах математики.

Давайте рассмотрим следующее олимпиадное задание:

Надо решить уравнение 5² *5⁴ *5⁶ *... * 5^2x =0,04^-28

вопрос: Что происходит при умножении степеней с одинаковыми основаниями?

ответ: Складываются их показатели.

2+4+6+...+2х=56

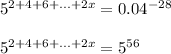
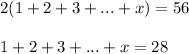
Левая часть уравнения это арифметическая прогрессия с первым членом   и разностью  . Найдем сумму



Подставим в уравнение

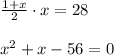
 Учитель: Так как мы ограниченны во времени, то не можем показать все разнообразие задач по прогрессиям на одном уроке. Хочется лишь отметить, что задачи на прогрессии встречаются во многих сферах человеческой жизни. Прогрессии действительно везде вокруг нас. С помощью прогрессий можно проводить вычисления результатов в спорте, в компьютерной игре, решения физических и геометрических задач. Можно объяснить суть финансовых пирамид. Прогрессии существуют даже в литературе!

Спасибо всем группам за отличную работу и интересные задачи.

4. Подведение итога урока. Рефлексия

- На этом уроке я постаралась вам показать, что необходимо очень внимательно относится к изучению тем по математике, так как эти знания вам могут пригодится в жизни. И не только чтобы успешно сдать экзамены.

Мне хочется, чтобы вы ответили на два вопроса:

1. Пригодятся ли мне в жизни знания о прогрессиях. Если да, то в каких областях.

2. Достаточно ли у Вас знаний по данной теме или Вам хочется узнать что-то еще

5. ДЗ

Дополнительные задачи.

Задача №: Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 р., а после двенадцатого повышения - 1650 р. Через сколько повышений первоначальная цена удвоилась? ( слайд 15)

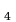Решение: (b )- арифметическая прогрессия, b =1200; b =1650;

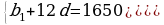
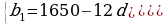
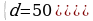
Так как цена товара увеличилась в два раза, то она стала равна 2100 рублей.

b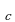 = 2b ; 2100 = 1050+50(n-1)

50(n-1) = 1050

n-1 = 21

n = 20

Ответ: через 20 повышений.

Задача№: Человек, заболевший гриппом, может заразить четырех человек. Через сколько дней заболеет все население поселка в количестве 341 человека?

Решение: (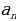 )- геометрическая прогрессия.
 = 1; q= 4. 
Найти 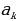=341, где k – порядковый номер дня, когда все в поселке заболеют.
=
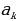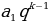
341=1
=341
Так как, 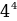=256, а =1024, то человек заразит всех в поселке уже вначале 5-го дня .
Ответ: 5 дней.

Задача № .Дима на перемене съел булочку. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 мин. происходит деление бактерий (они удваиваются). Сколько дизентерийных палочек будет в кишечнике через 6 часов? (Ответ: 7864290 шт.) (Решение: а₁=30; q=2; n=18; S₁₈-?)

Задача №: Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 р., а после двенадцатого повышения - 1650 р. Через сколько повышений первоначальная цена удвоилась? ( слайд 15)

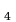Решение: (b )- арифметическая прогрессия, b =1200; b =1650;

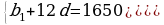
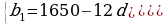
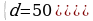
Так как цена товара увеличилась в два раза, то она стала равна 2100 рублей.

b = 2b ; 2100 = 1050+50(n-1)

50(n-1) = 1050 n-1 = 21 n = 20

Ответ: через 20 повышений.

Задача.Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв в день 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Решение. На первом этапе приёма капель число принимаемых капель в день представляет собой возрастающую арифметическую прогрессию с первым членом, равным 3, разностью, равной 3 и последним членом, равным 30. Следовательно,

этап, когда число капель в день возрастает продолжается   Суммарное число капель, принятых в этот период, представляет собой сумму арифметической прогрессии:

Затем в течение трёх дней пациент принимает ещё 

Последний этап приёма начинается с того момента, когда пациент уменьшит число принимаемых капель на 3, то есть примет в день 27 капель. Этот этап длится   Аналогично первому этапу:

Таким образом, за весь курс приёма пациенту нужно принять 165 + 90 + 135 = 390 капель. То есть нужно приобрести не меньше   пузырьков лекарства. Минимальное количество пузырьков лекарства — 2.

Ответ: 2.

Задача №

Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Население поселка 2200 человек. Через сколько дней заболеют гриппом все жители поселка? (Ответ: через 7 дней.) (Решение: b₁=1; bn=2200, q=4, n-?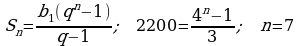

После решения задачи и её обсуждения учащийся выступает с докладом о профилактике гриппа и простудных заболеваний.

Задача №

Дима на перемене съел булочку. Во время еды в кишечник попало 30 дизентерийных палочек. Через каждые 20 мин. происходит деление бактерий (они удваиваются). Сколько дизентерийных палочек будет в кишечнике через 6 часов? (Ответ: 7864290 шт.) (Решение: а₁=30; q=2; n=18; S₁₈-?)

Задача №

В нормальном состоянии объем печени человека равен 2,2 дм³. Через 25 дней с момента заражения вирусным гепатитом она увеличивается до 3,4 дм³. На сколько увеличивается печень ежедневно? (Ответ: 0,05 дм³= 50 см³) (Решение: а₁=2,2; n=25; а_n=3,4; d-?)

Задача №

Каждый курильщик выкуривает в день в среднем 8 сигарет. После выкуривания первой сигареты в легких оседает 0,0002 г. никотина и табачного дегтя. С каждой последующей сигаретой это количество увеличивается на 0,000001 г. Какое количество вредных веществ оседает в легких за год? (Ответ: 4,846 г.). (Решение: d=0,000001; a₁=0,0002; n=365*8=2920; S₂₉₂₀-?)

Задача № 4 Высота саженца 60 см,

первые полгода она увеличивается

ежемесячно в среднем на 4 см. Каким

будет высота саженца через 6 месяцев?

- И еще одна ступень: «биология».

Дано: (а_n) – арифм. прогр.; a₁=60 см; d= 4

см

Найдите S₆=?

Решение: a_n=a₁+d (n−1)

a₆=60+4 (6−1 )=80

6. Рефлексия

: Отгадайте загадку

• Оно длиннее всего на свете — и короче. Быстрее всего — и медленнее. Самое дробное — и самое неразрывное. Его меньше всего ценят, но больше всего сожалеют о его отсутствии. Без него ничего не может быть сделано . 

• Скоро вам предстоит сдавать выпускные экзамены, а чтобы успешно их сдать, нужно регулярно готовиться. Психологи рекомендуют начать подготовку с занятий 15 мин в день, увеличивая каждую неделю время занятий на 5 мин в день, но не превышая время 1час 35 мин.
• Сколько времени следует уделить подготовке к экзамену на 5-й неделе?
• И на какой неделе ученик достигнет максимального времени подготовки?

15 мин,20 мин,25 мин,30 мин, 35 мин , 40 мин,45 мин,50 мин,55 мин,60 мин, 65 мин,70 мин,75 мин,80 мин, 85 мин, 90 мин, 95 мин

« Прогрессии в окружающей нас жизни »

Проблемный вопрос

Зачем нужно изучать прогрессии?

--Действительно ли прогрессии играют большую роль в повседневной жизни?

--Действительно ли прогрессия является инструментом для решения реальных задач в различных сферах человеческой жизни?

Прогрессия – движение вперед

Цели урока:

• Убедиться в том…
• что раздел математики «Прогрессии» является неотъемлемой частью общечеловеческой культуры;
• прогрессия – это не просто математическая «игрушка», а мощный инструмент для решения реальных задач в различных сферах человеческой жизни;
• что знания о прогрессиях были известны еще в древнем мире;
• что знания по прогрессиям необходимы в банковских расчетах, в микробиологии и медицине, в строительстве и даже спорте.
• - что задания по прогрессиям встречаются в олимпиадных заданиях .

Для какой прогрессии записаны формулы в каждом из столбцов?  

История

• Термин «прогрессия» имеет латинское происхождение и был введен римским автором Боэцием в 6 веке.

• В развитие теории о прогрессиях внесли свой вклад такие ученые, как Архимед, Пифагор и его ученики, французские математики Леонард Фибоначчи и Баше де Мезириак, немецкие математики М. Штифель, Н.Шюке и К. Гаусс.

В трудах АРХИМЕДА (ок. 287-212 гг. до н.э.) излагаются первые сведения о прогрессиях.

Пифагор ( IV в. до н. э.) и его ученики рассматривали последовательности, связанные с геометрическими фигурами.

Архимед

Вопросами последовательности занимался Леонардо Пизанский (Фибоначчи). Наиболее известной из сформулированных Фибоначчи задач является "задача о размножении кроликов", которая привела к открытию числовой последовательности 1, 1, 2, 3, 5, 8, 13, ..., именуемой впоследствии "рядом Фибоначчи".

Леонардо Пизанский

(Фибоначчи)

• Задача №1 (из учебника Магнитского):

Богач-миллионер возвратился из отлучки необычайно радостный: у него была по дороге счастливая встреча, сулившая большие выгоды. Рассказывает он домашним: «Вот и на мою деньгу денежка бежит. Повстречался мне в пути незнакомец, из себя не видный. Предложил выгодное дельце, что у меня дух захватывает». «Сделаем,- говорит, - такой уговор. Я буду целый месяц приносить тебе ежедневно по сотне тысяч рублей. Недаром, разумеется, но плата пустяшная. В первый день я должен по уговору заплатить – смешно сказать – всего 1 копейку. А за вторую сотню тысяч – 2 копейки. И так целый месяц, каждый день вдвое больше предыдущего. Находим выгодность сделки.

Кому выгодна сделка?

Приходит как-то раз к одному богатому

купцу мужик и предлагает сделку.

«Давай, говорит, в течение месяца я

буду приносить тебе каждое утро по

100 000 руб., а ты мне взамен в первый

день отдашь 1 коп., а в каждый последующий в 2 раза больше. Во второй день - 2 коп.,

в третий - 4 коп. и т.д.»

Подумал купец и подписал договор.

10

Сумма, которую получит богач

S =100 000руб*30дней=3 000 000руб

Сумма, которую получит незнакомец

1-ый день- 1 коп

2-ой день- 2 коп

3-ий день- 4 коп

4-ый день- 8 коп

5-ый день- 16 коп

6-ой день- 32 коп

7-ой день- 64 коп

8-ой день- 128 коп

9-ый день- 256 коп

10-ый день- 512 коп

11-ый день- 1 024 коп

12-ый день- 2 048 коп

13-ый день- 4 096 коп

14-ый день- 8 192 коп

15-ый день- 16 384 коп

…………………………………… ..

Путь не рациональный.

13

Дано: b 1 =1; q =2

Найти: S 30 - ?

Решение

Сумма, отданная незнакомцу в последний день

b 1 = 0,01; q = 2

b 30 = b 1  q 29 = 0,01  2 29 = 5 368 709,12 =5 368 709 рублей 12 копеек

Сумма, полученная незнакомцем от миллионера за 30 дней

• b 1 = 0,01; q = 2
• S = 10 737 418 р. 23 к. = 11 млн. руб
• . Незнакомец заплатил богачу: 30∙100 тыс = 3000 тыс. = 3000000 рублей .
• Убыток 11000000 – 3000000=8000000 рублей.

S =

b 1 (q n -1)

=

q - 1

0,01 (2 30 – 1)

2 - 1

Сравним доходы

Купец получил – 3 000 000 р.

Мужик – 10 737 418 р. 23 к.

Разница составляет – 7 737 418 руб. 23 коп.

.

Группа экономистов

Группа экономистов

Задача №2: Предприниматель взял в банке кредит 500000 рублей под 20% годовых. Какую сумму должен он вернуть через 3 года?

.

Группа экономистов

Задача №2: Предприниматель взял в банке кредит 500000 рублей под 20% годовых. Какую сумму должен он вернуть через 3 года?

Решение. Давайте обозначим а= 500000 , тогда

• -в конце первого года он должен будет отдать , а+0,2а=1,2а
• -в конце второго года 1,2а+0,2∙1,2а=1,2а(1+0,2)=1,2²∙а =1,44а
• -в конце третьего года он должен будет вернуть
• 1,44а+0,2∙1,44а=1,44а(1+0,2)= 1,2³∙а=1,728∙500000=864000 рублей
• Вопрос: Какая получается прогрессия?
• Ответ : геометрическая
• Вывод : значит если вы решите когда-нибудь взять кредит, то вспомните что вам отдать надо будет сумму, которая вырастет в геометрической прогрессии.

Группа экономистов

Задача №3:

Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 р., а после двенадцатого повышения - 1650 р. Через сколько повышений первоначальная цена удвоилась?

Первоначальная цена товара на торгах повышалась несколько раз на одно и то же количество рублей. После третьего повышения цена равнялась 1200 р., а после двенадцатого повышения - 1650 р. Через сколько повышений первоначальная цена удвоилась?

Физкультминутка для глаз

Группа микробиологов и медиков

Группа микробиологов

• Задача№5: Каждое простейшее одноклеточное животное инфузория–туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 1920?

• Задача№5: Каждое простейшее одноклеточное животное инфузория–туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 1920?

Решение:

b1 - первоначальное количество инфузорий;

b2 - Количество инфузорий после первого деления;

b3 - количество инфузорий после второго деления;

...

b7 = 1920 - количество инфузорий после шестого деления.

Количество инфузорий постоянно увеличивается в 2 раза, значит мы имеем дело с геометрической прогрессией со знаменателем q = 2.

Запишем формулу n-ого члена геометрической прогрессии и подставим в нее всё, что нам известно.

b n  = b 1 q n-1     (n = 7);

1920 = b 1  · 2 7-1

b1 = 1920 : 64 = 30.

Ответ: 30.

Группа микробиологов и медиков

Задача № 6: Задача из сборника ОГЭ Больной принимает гомеопатическое лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Решение. Составим математическую модель задачи : 5, 10, 15, … ,40, 40, 40, 35, 30, … ,5

возрастающая

арифметическая

прогрессия

а 1 =5, d= 5

убывающая

арифметическая

прогрессия

с 1 =40, d= -5

Решение. Составим математическую модель задачи : 5, 10, 15,20,25,30,35,40, 40, 40, 35, 30, … ,5

убывающая

арифметическая

прогрессия

с 1 =40, d= -5

возрастающая

арифметическая

прогрессия

а 1 =5, d= 5

а п =а 1 + d(n-1) , 40=5+5(п-1), п=8, S п = (( a 1 +a п )n)/2 ,

S 8 =(5+40) · 8:2=180 ,

Решение. Составим математическую модель задачи : 5, 10, 15,20,25,30,35,40, 40, 40, 35, 30, … ,5

возрастающая

арифметическая

прогрессия

а 1 =5, d= 5

убывающая

арифметическая

прогрессия

с 1 =40, d= -5

а п =а 1 + d(n-1) , 40=5+5(п-1), п=8, S п = (( a 1 +a п )n)/2 ,

S 8 =(5+40) · 8:2=180 ,

а п =а 1 + d(n-1) , 5=40-5(п-1), п=8, S п = (( a 1 +a п )n)/2 ,

S 8 =(5+40) · 8:2=180

Решение. Составим математическую модель задачи : 5, 10, 15, … ,40, 40, 40, 35, 30, … ,5

возрастающая

арифметическая

прогрессия

а 1 =5, d= 5

убывающая

арифметическая

прогрессия

с 1 =40, d= -5

а п =а 1 + d(n-1) , 40=5+5(п-1), п=8, S п = (( a 1 +a п )n)/2 ,

S 8 =(5+40) · 8:2=180 ,

180 капель больной принимал по схеме в первый период и столько же второй период. И еще 40 капель. Всего он принял 180+4+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства

а п =а 1 + d(n-1) , 5=40-5(п-1), п=8, S п = (( a 1 +a п )n)/2 ,

S 8 =(5+40) · 8:2=180

Прогрессия в олимпиадных задачах

• Решите уравнение

5 2 *5 4 *5 6 *... * 5 2 x =0,04 -28

Интересные факты

• Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растет по геометрической прогрессии.
• Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.
• Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
• Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.
• Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.

Рефлексия

Работая над проектом, я понял …

Работая над проектом, я узнал …

Работая над проектом, мне понравилось …

Работая над проектом, я научился …

Понравилась работа ?

Какие трудности были во время коллективной работы?

Физкультминутка для глаз

Берегите зрение!