Основы теории множеств

Раздел «Основы теории множества»

Тема: Понятие Множества. Подмножество.

Дискретная математика – область математики, изучающая дискретные математические объекты и структуры.

Раздел 1. Основы теории множеств. Теория множеств — раздел математики, в котором изучаются общие свойства множеств. Любые объекты, которые мы мыслим вместе и которые мы можем объединить либо списком, либо при помощи общего признака, будут составлять множество.

Для сокращенной записи будем использовать следующие символы:

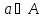– а является элементом множества А;

– пустое множество;

{a, d, с} – множество, состоящее из трех элементов a, d и с;

{x|Р(x)} – множество, состоящее из таких элементов х, для которых истинно утверждение Р(х);

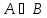– объединение множеств A и В;

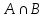– пересечение множеств А и В;

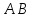– А является подмножеством В;

А \ В – разность множеств А и В;

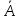– дополнение множества А до универсального множества;

U – универсальное множество;

A*B – декартово произведение множеств А и B;

a R b – между a и b существует бинарное отношение R.

Множество – основное понятие математики и поэтому не определяется через другие. Обычно под множеством понимают совокупность предметов, объединенных по общему признаку. Так, можно говорить о множестве студентов в группе, множестве букв русского алфавита и т.д. 

Множества принято обозначать прописными буквами латинского алфавита: А, В, С, ..., Z.

Множество считается заданным, если относительно каждого объекта можно сказать, принадлежит он данному множеству или нет. Поэтому обычно говорят о множестве как о наборе предметов (элементов множества), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

Пустое множество ( ) не содержит ни одного элемента и обозначается буквой Ø.

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Примеры: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Объекты, из которых образовано множество, называют его элементами. Количество элементов конечного множества называют его мощностью.

Мощность конечного множества  – число его элементов. Мощность бесконечного множества равна ∞.

Способы задания множеств.

Если объект a является элементом множества A, то говорят, что a принадлежит A, и записывают.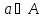

Множество может быть задано следующим образом:

1. Перечислением всех его элементов по их названиям (так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

Множество можно задать перечислением всех его элементов в любом порядке. Если множество A, например, состоит из первых четырех букв русского алфавита, то записывают A = {а, б, в, г}.

1. Заданием общей характеристики (общих свойств) элементов данного множества (например, множество рациональных чисел, собаки, семейство кошачьих и т.д.);

Множество может быть задано с помощью характеристического свойства, т.е. такого свойства, которым обладают все элементы данного множества и не обладают никакие другие объекты. При данном способе задания множество может быть записано так: в фигурных скобках пишут сначала обозначение элемента, затем проводят вертикальную черту, после которой записывают свойство, которым обладают элементы данного множества. Например, множество А натуральных чисел, меньших 5, запишется так: А = {ххN, х 

Круглая скобка, прилегающая к числу, означает, что это число не включено в промежуток, а квадратная – что число включено. Если промежуток связан с бесконечностью, то с символом бесконечности ставят круглую скобку.

Например, запись 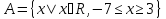означает, что множество A состоит из всех действительных чисел, больших или равных −7 и меньших 3.

Множество, состоящее из чисел, называют числовым множеством. Для числовых множеств в математике приняты специальные обозначения:

N – множество натуральных чисел;

N₀ – множество целых неотрицательных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

R – множество действительных чисел.

Если элемент x является одним из элементов множества A, то пишут x  A, если все элементы множества A являются также и элементами множества B, то говорят, что множество A является подмножеством множества B и пишут A  B.

Пустое множество является подмножеством любого множества: Ø  A, любое множество является своим собственным подмножеством: A  A.

Булеаном множества М назовем множество всех его подмножеств.

Задание1.

Используя понятие характеристического свойства, зададим следующие множества:

A = {б, в, г, д, ж, з, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ};

B = {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый};

C = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}.

Решение. Множества A, B и C заданы способом перечисления элементов. Используя характеристические свойства, указанные множества можно задать следующим образом:

A – множество согласных букв русского алфавита;

B – множество цветов радуги;

C – множество дней недели.

Задание2.

Рассмотрим множество 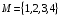. Составим все подмножества множества М.

, , ,

, , , , , ,

, , , ,

.

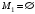
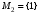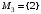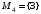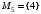
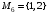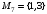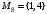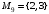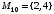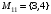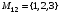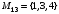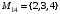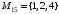Подмножества 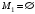и являются несобственными подмножествами множества М, остальные – собственные подмножества. Всего мы нашли 16 различных подмножеств множества М. Это число равно .

Доказано, что если множество состоит из п элементов, то у него 2^п различных подмножеств.

Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.

Каждый элемент входит в множество только один раз. Например, множество различных букв в слове «математика» запишется так: {м, а, т, е, и, к}.

Задание3.

Рассмотрим множества, состоящие из букв слов:

; ; ; .

Множества А, В и С имеют равные мощности: , а мощность множества D меньше . При этом множества А и В равны, а множества А и С – эквивалентны.

Задание4.

Изобразим на числовой прямой элементы следующих множеств:

а) ;

б) ;

в) ;

г) .

Решение.

а) Элементами множества A являются натуральные числа от 3 до 10, т.е. A = {3, 4, 5, 6, 7, 8, 9, 10}. Изобразим эти числа точками на числовой прямой.

б) Множество B состоит из всех целых чисел, находящихся в промежутке от −4 до 6, т.е. B = {−4,−3,−2,−1, 0, 1, 2, 3, 4, 5}. Число 6 не принадлежит множеству B, поскольку x B изображается так, как показано на рисунке

в) Множество C состоит из всех действительных чисел, принадлежащих промежутку от −5 до 8. Причем число −5 принадлежит множеству C, а число 8 не принадлежит. Изобразим множество C = [−5, 8) на числовой прямой.

г) Чтобы найти множество D, решим неравенство . Данное неравенство равносильно следующему: . Точки и являются критическими точками, поскольку в них выражение, стоящее в левой части неравенства, меняет знак. Изобразим эти точки на числовой прямой. Далее, применяя метод интервалов, находим, что неравенству удовлетворяют числа x2 или x 2.

Таким образом, множество D состоит из двух промежутков .

Задание5.

Задайте множество другим способом (если это возможно):

а) А = {х| xN, х ≤ 9};

б) А = {-4, -3, -2, -1, 0, 1, 2, 3, 4};

в) А = {х| xR, – 3 = 0}.

Решение:

а) Элементами множества А являются натуральные числа, которые меньше 9 и само число 9, значит, А = {1, 2, 3, 4, 5, 6, 7, 8, 9};

б) А = {х| xZ, |x| ≤ 4} – множество целых чисел, модуль которых не больше четырех;

в) Элементами множества А являются корни уравнения – 3 = 0, значит, А = {}.

Тема: Диаграммы Венна. Отношения между множествами.

Для наглядного представления множеств, отношений между множествами и операции над ними применяют своего рода диаграммы. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него – кругов Эйлера, представляющих множества.

Вместо кругов Эйлера определенные множества изображают любые другие замкнутые фигуры, и такую иллюстрацию называют диаграммами Венна.

Для рассуждений, связанных с множествами, будем использовать язык диаграмм Эйлера Венна.

Область, представляющую то подмножество, которое нас интересует, отметим штрихами.

Рис.1 Первая диаграмма соответствует универсальному множеству U, вторая – его пустому подмножеству, третья – произвольному множеству А.

Пусть имеем множества A и B. Элемент x называют общим элементом этих множеств, если xA и xB. Если множества A и B имеют общие элементы (хотя бы один), то говорят, что они пересекаются или находятся в отношении пересечения.AB

Если каждый элемент множества B принадлежит множеству A, то записывают BA.

Если AB и BA, то множества A и B называют равными и обозначают A = B. Равные множества состоят из одних и тех же элементов. Все возможные случаи отношений между пересекающимися множествами представлены на рисунке 2.

Рис.2 Отношений между пересекающимися множествами

Если множества A и B не имеют общих элементов, то их называют непересекающимися. Диаграммы Эйлера–Венна для этого случая представлены на рисунке 3.

Рис.3 Непересекающиеся множества

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно множествам А и В, то говорят, что эти множества пересекаются.

Например, множества А = {1, 2, 3, 4} и В = {0, 3, 5} пересекаются, т.к. имеют общий элемент 3.

Множества А и В не пересекаются, если не имеют общих элементов. Множества А = {1, 2, 3, 4} и В = {0, 8, 5} не пересекаются.

Например, множества А = {1, 2, 3} и В = {2, 3, 1} равны, т.к. состоят из одинаковых элементов. Таким образом, множество не изменится, если переставить его элементы.

Объединение множеств A  B – множество, составленное из всех элементов обоих множеств A и B.

Например, Пусть А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7}, тогда А  В = {1, 2, 3, 4, 5, 6, 7}.

Рис.4 Объединение множеств

Разность множеств A \ B – множество, составленное из тех элементов A, которые не входят в B. Если А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7}, тогда А \ В = {1, 2, 3}..A\B=A∩

Рис.5 Разность множеств

Дополнение = U \ A – множество элементов универсального множества, не принадлежащих A. Например, если U – множество цифр, а множество А = {1, 2, 3, 4, 5}, то A’= {6, 7, 8, 9, 0}. Двойное дополнение А=А

Рис.6 Дополнение множеств

Симметрической разностью А и В называется множество , состоящее из элементов множеств А или В, но не принадлежащих этим множествам одновременно.

Рис.7 Симметрическая разность множеств

Пример: Если , , то .

Задание1. Определим, в каких отношениях находятся множества A и B. Изобразим эти отношения при помощи диаграмм Эйлера–Венна, если:

а) A – множество гласных букв русского алфавита; B – множество звонких согласных.

б) A – множество натуральных чисел, кратных 3; B – множество натуральных чисел, кратных 9.

Решение.

а) Поскольку множества A и B не имеют общих элементов, то они не пересекаются.

Поэтому на диаграммах Эйлера–Венна они будут изображаться так, как показано выше.

б) Представим множества A и B в следующем виде:

A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36,...}; B = {9, 18, 27, 36, ...}.

Из приведенных записей очевидно, что множества A и B пересекаются. Кроме того, каждый элемент множества B принадлежит множеству A, т.е. BA. Соответствующая диаграмма представлена на рисунке.

Задание2. Приведем примеры множеств, находящихся в отношениях, представленных на диаграммах.

Решение. 1. Для случая, представленного на рисунке а, можно рассмотреть:

1. – множество чисел, кратных 2;

2. – множество чисел, кратных 3;

C – множество чисел, кратных 5.

Множества A и B пересекаются, так как содержат общие элементы – числа, кратные 6. Аналогично, множества B и C пересекаются, так как содержат числа, кратные 15. Множества A и C также содержат общие элементы – числа, кратные 10. Общими элементами для всех трех множеств A, B и C являются числа, кратные 30.

2. Примерами множеств, представленных на диаграмме б, могут служить:

1. – множество частей речи;

2. - множество существительных;

C – множество предлогов.

3. Диаграммы Эйлера–Венна будут иметь вид, представленный на рисунке в, если, например:

A – множество многоугольников;

B – множество равносторонних треугольников; C – множество равнобедренных треугольников; D – множество четырехугольников.

Задание3. О каких множествах говорится в утверждении «Все студенты нашей группы участвовали в праздничной линейки»? Выделите эти множества и установите, в каких отношениях они находятся.

Решение. Выделим и обозначим множества, о которых идет речь в данном утверждении: это множество A – студентов некоторой группы и множество B – участников праздничной демонстрации. В данном утверждении сообщается, что все элементы множества A являются также элементами множества B. По определению отношения включения это означает, что AB.

Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А.

Задание4.

Рассмотрим множество M{2,5,6,7,10,11}. Составим все подмножества множества М.

Задание5.

Задать с помощью перечисления элементов множества A U B, A ∩ B, A \ B, B \ A, если A = {3, 7, 2, 4,1}, B = {5, 2, 8, 3}.

Решение. Пользуясь только определениями операций объединения, пересечения, разности множеств, получаем: A U B = {1, 2, 3, 4, 5, 7,8}, A ∩ B = {2, 3}, A \ B = {1, 4, 7}, B \ A = {5,8}.

Задание6.

Вычислить:

_А)

_Б)

_В)

_Г)

Задание7.

Запишите множество дробей , числителем которых являются числа из множества , а знаменателем – числа из множества

Задание8.

Даны множества A₁ = {a, b, c}; A₂ = {c, d, e, f}; U = {a, b, c, d, e, f}. Осуществить над множествами операции: а) объединения; б) пересечения; в) разности; г) дополнения.

Решение. а) объединение множеств А1 и А2 содержит все элементы, принадлежащие множествам А1 и А2: A₁ A₂ ={a,b,c,d,e, f};

б) пересечение множеств А1 и А2 содержит только элементы, принадлежащие и первому, и второму множествам: A₁ A₂ ={c};

в) используя определение разности множеств, получаем: A₁ \ A₂ ={a,b}, A₂ \ A₁ ={d,e, f};

г) дополнение A₁ содержит только те элементы множества U, которые не принадлежат А1: A₁ =U \ A₁ ={d,e, f}. Аналогично, =U \ A₂={a,b}.

Задание9. Даны множества А = { a , b , c , d , e , f , k } и  В = { a , c , e , k , m , p }. Найдите       А ∪ В ,  А ∩ В ,   А \ В , В \ А .

Ответ: А ∪ В={ a , b , c , d , e , f , k  , m , p  }

А ∩ В ={ a , c , e , k }

А \ В={  b , d , f  }

В \ А = {m , p }.

Задание10. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.

Решение:  Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.

Тема: Операции над множествами.

Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел. Используя эти операции можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только затем операции объединения и разности. Для изменения порядка в выражении используют скобки.

Задание1. Определите порядок выполнения действий в следующих выражениях: а) А  В  С; б) А  В  С  D; в) А  В  С; г) А  В  С  D.

Задание2. Постройте три круга, представляющие попарно пересекающиеся множества А, В и С, и отметьте штриховкой области, изображающие множества: а) А  В  С; б) (А  В)  С; в) А  В  С; г) А  В  С; д) (А  В)  С; е) (А  С)  (В  С). Для каждого случая сделайте отдельный рисунок.

Задание3. Среди следующих выражений найдите такие, которые представляют собой равные множества: а) Р  М  К; б) Р  (М  К); в) Р  М  Р  К; г) (Р  М)  К; д) Р  (М  К); е) (М  Р )  (Р  К).

Задание4. Найдите разность множеств А и В, если: а) А = 1, 2, 3, 4, 5, 6, В =  2, 4, 6, 8, 10; б) А = 1, 2, 3, 4, 5, 6, В = ; в) А = 1, 2, 3, 4, 5, 6, А = 1, 2, 3, 4, 5, 6; г) А = 1, 2, 3, 4, 5, 6, В = 6, 2, 3, 4, 5, 1.

Задание5. Доказать справедливость следующего равенства и проверить результат на диаграмме Эйлера-Венна

Решение: Преобразуем по очереди левую и правую части данного равенства:

. Заменили разность на пересечение с дополнением.

= ) = =

Задание6. Используя свойства операций, упростите выражения и проверьте правильность с помощью диаграмм Эйлера-Венна:

2.

3. А\(А\С)

4.

5.

6. В

Тема: Теоретико-множественные преобразования. Декартово произведение множеств.

Используя две цифры, например, 3 и 5, можно записать четыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов a и b, принято записывать, используя круглые скобки: (a, b). Элемент а называют первой координатой (компонентой) пары, а элемент b – второй координатой (компонентой) пары.

Пары (а; b) и (с; d) равны в том и только в том случае, когда а = с и b = d.

В упорядоченной паре (а; b) может быть, что а = b. Так, запись чисел 33 и 55 можно рассматривать как упорядоченные пары (3; 3) и (5; 5).

Упорядоченные пары можно образовывать как из элементов одного множества, так и двух множеств. Такие упорядоченные наборы называют кортежами. Так, набор {1, 5, 6} есть кортеж длины 3, так как в нем три элемента.

Пусть, например, А = {1, 2, 3}, В = {3, 5}. Образуем упорядоченные пары так, чтобы первая компонента принадлежала множеству А, а вторая – множеству В. Если мы перечислим все такие пары, то получим множество: {(1; 3), (1; 5), (2; 3), (2; 5), (3; 3), (3; 5)}.

Видим, что имея два множества А и В, мы получили новое множество, элементами которого являются упорядоченные пары чисел. Это множество называют декартовым произведением множеств А и В.

Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают АхВ. Используя это обозначение, определение декартова произведения можно записать так: АВ = {(x;y) | xA, yB}.

Декартовым квадратом множества А называют декартово произведение множества А на множество А (т.е. само на себя).

Задание1. Известно, что АВ={(2, 3), (2, 5),    (2, 6), (3, 3), (3, 5), (3, 6)}. Установим, из каких элементов состоят множества А и В. Так как первая компонента пары декартового произведения принадлежит множеству  А, а вторая – множеству  В, то данные множества имеют следующий вид:  А={2, 3}, B={3, 5, 6}.

Перечислим элементы, принадлежащие множеству АхВ, если 
А={a, b, c, d},   B=A. Декартово произведение АхВ={(a, a), (a, b), (a, c), 
(a, d), (b, a), (b, b), (b, c), (b, d), (c, a), (c, b), (c, c), (c, d), (d, a), (d, b) ,(d, c), (d, d)}.

Задание2.

Пусть даны множества А={2, 3}; А={3, 4, 5}; A={7, 8}. Декартово произведение ААА={ (2, 3, 7), (2, 3, 8), (2, 4, 7), (2, 4, 8), (2, 5, 7), 
(2, 5, 8),(3, 3, 7), (3, 4, 7), (3, 3, 8), (3, 4, 8), (3, 5, 7), (3, 5, 8)}.

Задание3.

Даны множества: А₁= 2, 3, А₂= 3, 4, 5, А₃ = 6, 7. Найти А₁ А₂ А₃.

Решение: Элементами множества А₁ А₂ А₃ будут кортежи длины 3 такие, что первая их компонента принадлежит множеству А_1, вторая – множеству А₂, третья – множеству А₃.

А₁ А₂ А₃ =(2,3,6), (2,3,7), (2,4,6), (2,4,7), (2,5,6), (2,5,7), (3,3,6), (3,3,7),(3,4,6), (3,4,7), (3,4,7),(3,5,6), (3,5,7).

Задание4. Элементами множеств А и В являются пары чисел: А = (1,12), (2, 9), (3,6), (4, 3), (5, 0), В = (1,9), (2,7),(3,6), (4,7), (5,0). Найдите пересечение и объединение данных множеств.

Задание5.

Запишите различные двузначные числа, используя цифры 3, 4 и 5. Сколько среди них таких, запись которых начинается с цифры 3? 

Задание6.

Перечислите элементы декартова произведения   В, если: а) А = a,b,c, d, B =  b, k, l; б) А = В = a, b, c; в) А = a, b, c, В = .(Декартово произведение пустого множества на любое множество равно пустому множеству.)

Задание7.

Даны множества А = 1, 3, 5 и В = 2, 4. Перечислите элементы множеств   В и В  А. Верно ли, что: а) Множества   В и В  А содержат одинаковое число элементов; б) Множества   В и В  А равны?

Задание8. Найдите декартово произведение множеств А и В, если: а) A = {т; р}, В = {e, f, k}; 6) A = B = {3, 5}.

Задание9. Даны множества А = 1, 3, 5 и В = 2, 4. Перечислите элементы множеств   В и В  А. Верно ли, что: а) Множества   В и В  А содержат одинаковое число элементов; б) Множества   В и В  А равны?

Задание10. Перечислите элементы декартова произведения   В, если: а) А = a,b,c, d, B =  b, k, l; б) А = В = a, b, c; в) А = a, b, c, В = .

Тема: Бинарные отношения. Соответствия между множествами

Отношения – один из способов задания взаимосвязей между элементами множества.

При этом отношения отдельных объектов называются унарными отношениями, отношения, относящиеся к парам объектов, - бинарными отношениями, отношения, относящиеся к наборам из n объектов, - n-арными отношениями. Ниже мы ограничимся рассмотрением лишь бинарных отношений.

Всякое подмножество декартова произведения АхВ называется бинарным отношением.

Для обозначения бинарного отношения принимают знак R. Поскольку R – это подмножество множества AxB, то можно записать .

Задание 1. Выпишите упорядоченные пары, принадлежащие бинарным отношениямR₁ и R₂, заданными на множествах A={1.3.5.7} и B={2.4.6}:

R₁ ={(x,y):х+у=9}, R₂ ={(x,y):хy}

R₁ состоит из пар:{(3,6),(5,4),(7,2)} .

Подмножество R₂ ={(1,2),(1,4),(1,6),(3,4),(3,6),(5,6)}

Задание 2. Пусть А={1,2,3,4,5,6,7}, В={1,2,3} .

Пусть R₁ задано на АхВ перечислением упорядоченных пар:

R₁ ={(1,2),(1,3),(4,2),(6,1)}

Бинарное отношение R₂ на множестве АхВ задано с помощью правила: упорядочена пара (а,b) принадлежит R₂, если a делится на b.

Тогда R₂ состоит из пар: {(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),(7,1),(2,2),(4,2),(6,2),(3,3),(6,3)}.

Свойства бинарных отношений:

• Бинарное отношение R на множестве МхМ называется рефлексивным, если для любого элемента a из M пара (a, a) принадлежит R, т.е. имеет место аRа для любого a изM:.

• Симметрия отношений. Пусть между элементами аи b имеется отношение R. Переставим местами a и b. Если при этом отношение R сохранится, то такое отношение симметричное. т.е. (a, b) принадлежит R и (b, a)принадлежит R.

• Транзитивность отношений. Отношение R в множестве М называется транзитивным, если из aRb и bRc следует aRc.

• Отношения эквивалентности. Если отношение R в множестве М обладает свойствами рефлексивности, симметричности и транзитивности, то оно называется отношением эквивалентности.

Задание3.

На множестве Х=0, 3, 6, 9, 12, 15, 18 задано отношение R. Перечислите пары чисел, связанных этим отношением

а) R – « х больше у в 3 раза»; б) R – « х больше у на 3».

Задание4.

На множестве Х = 2, 4, 6, 8 рассматриваются отношения «х = у», «ху» и «х больше у на 2». Какое из приведенных ниже подмножеств множества Х  Х задает данные отношения:

а) (4,2),(6,2),(8, 4),(8,6),(2,2),(4,4),(6,6),(8,8);

б) (4,2),(6,4),(8, 6);

в) (2,2),(4,4),(6,6),(8,8).

Задание5.

Задайте следующие соответствия для множеств хХ, у У, парами (х;у). Где Х={1, 2, 3, 4, 5}; У={6, 7, 8, 9, 10, 11, 12}:

а) x делит y (без остатка),

б) x меньше y,

в) x равно y,

г) у-х=2

Задание6.

Найдите декартов квадрат множества X = {6, 4, 3, 2}. Задайте бинарное отношение "первое число делится на второе" парами.

Задание7.

Найдите декартов квадрат множества X = {8, 4, 3, 1}. Задайте бинарное отношение "первое число делит второе" парами

Задание8.

На множестве M=[1,5] построить бинарное отношение R, такое что а делится на b без остатка.

Ответ: Получаем R={(1,1), (2,2), (3,3), (4,4), (5,5), (2,1), (3,1), (4,1), (5,1), (4,2)}.

Задание9. Выпишите упорядоченные пары, принадлежащие бинарным отношениямR₁ и R₂, заданными на множествах A={2,6,8,12} и B={3,6,8,9}:

R₁ ={(x,y):х+у=11}, R₂ ={(x,y):хy}

Задание10. На множестве Х=0, 3, 6, 9, 12, 15, 18 задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R – « х больше у в 3 раза»; б) R – « х больше у на 3».

Понятие соответствия между множествами

В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств.

Пример 1. а) (17 – 1) : 4; б) (12 + 18) : (6-6); в) 27 + 6.

Пример 2. 1) 2+х =6; 2) х-7=4; 3) 2х=8.

В первом примере мы установили соответствие между заданными выражениями и их числовыми значениями. Во втором выяснили, какое число является решением уравнения.

Все эти соответствия имеют общее – во обоих случаях мы имеем два множества: в первом – это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором – это множество из трех уравнений и множество N натуральных чисел.

Связь (соответствие) между этими множества можно представить наглядно, при помощи графов.

1 2

Полученные множества показывают, что любое соответствие между двумя множествами Х и У можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упорядоченные пары – это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.

Определение. Соответствием между множествами Х и У называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами S.

Способы задания соответствий

Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристическое свойство элементов этого подмножества.

Задание 11. Соответствие между множествами Х = 1, 2, 4, 6 и У = 3, 5 можно задать: 1) при помощи предложения с двумя переменными: а  в при условии, что а  Х, в  У; 2) перечислив пары чисел, принадлежащих подмножеству декартова произведения ХУ: (1,3),(1,5),(2,3),(2,5),(4,5). К этому способу задания относят также задание соответствия при помощи графа и графика.

у

Х У 5   

3  

1 2 4 х

Соответствие обратное данному

Задание 12. Пусть S – соответствие «больше на 2» между множествами Х = 4, 5, 8, 10 и У = 2, 3, 6. Тогда S = (4,2), (5,3), (8,6) и его граф будет как на рисунке.

Соответствие обратное данному, - это соответствие «меньше на 2». Оно рассматривается между множествами У и Х, и чтобы его представить наглядно, достаточно на графе соответствия S

направление стрелок поменять на противоположное (См. рисунок).

Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: х S у.

Определение. Пусть S – соответствие между множествами Х и У. Соответствие S^-1 между множествами У и Х называется обратным данному, если у S^-1х тогда и только тогда, когда х S у. Соответствия S и S^-1 называют взаимно обратными.

Задание 13. А) Множества Х = 1,3,4,6 и Y = 0,1 находятся в соответствии S = (1,1), (3,0), (3,1), (4,0), (4,1), (6,1). Задайте соответствие S^-1, обратное соответствию S, и постройте на одном чертеже их графики.

Б) Задайте при помощи графа соответствия между множествами Х = а, б, с и Y = 2, 4, 6, а так же обратное соответствие.

В) Пусть даны множества A = {2,4,6,8}, B = {3,5,7}, C = {6,9,12,15} и соответствия S= { (a,b) a b } A xB, = {(b,c) c = 3b } Bx C. Представить соответствия графически.

Задание 14. Изобразите на координатной плоскости декартово произведение А_В, если;

а) А = {1, 2, 3}, В = [3, 5]; б) А = [1, 3], В = [3, 5];

в) А = R, В = [3, 5]; г) А = R, В = R.

Решение. а) Так как множество А состоит из трех элементов, а, множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декартово произведений А_В будет состоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо 3, а вторая – любое действительное число из промежутка [3, 5]. Такое множество пар действительных чисел на координатной плоскости изобразится тремя отрезками (рис. 3).

Рис. 3

Задание 15. Даны множества: A₁ = {2, 3}, А₂ = {3, 4, 5}, A₃ = {6, 7}. Найти A_1хА_2хA₃.

Решение. Элементами множества A1_А2_A3 будут кортежи длины 3 такие, что первая их компонента принадлежит множеству A1, вторая – множеству A2, третья – множеству A3.

A_1хА_2хA₃ = {(2, 3, 6), (2, 3, 7), (2, 4, 6), (2, 4, 7), (2, 5, 6), (2, 5, 7), (3, 3, 6), (3, 3, 7), (3, 4, 6), (3, 4, 7), (3, 5, 6), (3, 5, 7)}.

8