Факультативный курс
«Математика в образах»
«Предмет математики настолько серьезен,
что полезно не упускать случая
сделать его немного занимательным».
Паскаль
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данный факультативный курс посвящен роли и месту идей современной математике в школьном курсе. Даже при беглом просмотре наших учебников заметить появление в них вопросов, относящихся к разделам современной математике: теории множеств и математической логики теоретико-множественные и логические основы школьной математики неоднократно обсуждалось на страницах методических журналов и газет.
«Содержание образования является одним из факторов экономического и социального прогресса общества и должно быть ориентировано на обеспечение самоопределение личности, создание условий для ее самореализации». ( Закон РФ «Об образовании», ст. 14)
«Реализация идеи профиля старшей ступени ставит выпускника основной ступени перед необходимостью совершения ответственного выбора – предварительного самоопределения в отношении профилирующего направления собственной деятельности». (Концепция профильного обучения).
Основные цели предпрофильной подготовки по математике
1. Выявление и формирование средствами математики направленности личности, ее профессиональных интересов.
2. Формирование деятельностных способностей к самореализации, самоопределению, рефлексии собственной деятельности.
3. Формирование и развитие мышления.
4. Овладение комплексом математических знаний, умений и навыков.
Поэтому считаю целесообразным включение предметно-ориентированного факультативного курса «Математика в образах» в систему предпрофильной подготовки учащихся по математике. Этот курс дополняет базовую программу, не нарушая ее целостности.
Математика возникла из практической деятельности человечества, здесь ее корни, стало быть, основные понятия математики можно пояснять на обыденных, общеизвестных примерах. Предлагаемый курс проводит эту мысль последовательно, демонстрируя ряд основополагающих концепций высшей математики с помощью простых доходчивых образов. Разговор о множествах начинается с игры в слова (алфавит-это множество букв), идея координат возникла из рассмотрения прямоугольной сети, свойства функций иллюстрируются через пословицы и т.п. Однако при всей кажущейся нестрогости изложения в основе данного курса лежит строгая логика предмета.
Описываемые понятия появляются в продуманной последовательности, их образы соответствуют точным определениям и складываются в систематическую картину.
Математика в образах, без строгих доказательств, без формул? Ведь это что-то вроде географии без карты или оперы без музыки! Что ж, опера без музыки в самом деле ничто. А что касается карт… Разве в них соль географии? Когда мы смотрим фильм, слушаем бывалого путешественника или путешествуем сами- разве мы не пополняем свои географические познания? К тому же это глубже воспринимается и гораздо интереснее, чем карты, хотя они подают информацию в предельно концентрированном виде.
Так и формулы. При всей их гибкости и емкости - не в них душа математики. В чем же загадочная душа математики? Обратимся к авторитету. Софья Ковалевская: «В математических работах, главное – содержание, идеи, понятия, а затем, для их выражения у математиков существует свой язык – это формулы».
Итак, содержание, идеи, понятия – первичны, а формулы – вторичны. Формулы – родной язык математики.
Программа курса содержит 8 блоков, связанных единой идеей. Построены они по модульному принципу.
При составлении данного курса учтены дидактические принципы организации учебно-воспитательного процесса предпрофильной подготовке:
Принцип деятельности. В процессе предпрофильной подготовки учащийся является не объектом, а субъектом деятельности.
Принцип вариативности. Самостоятельный выбор учащимися вариантов своего профиля.
Принцип минимакса. Разведение уровня подачи материала и уровня требований к его освоению. Разноуровневое содержание курсов по выбору.
Принцип психологической комфортности. Снятие стрессовых факторов учебного процесса, создание доброжелательной атмосферы, ориентированной на реализацию идей педагогики сотрудничесва.
Принцип творчества. Максимальная ориентация на творческое начало в учебной деятельности учащихся, приобретение им собственного опыта творческой деятельности.
ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЙ РАЗДЕЛ
ЦЕЛИ КУРСА:
1. Показать, что любая наука начинается с накопления экспериментальных факторов, установление устойчивых связей между явлениями, обычно называемых законами, Показать, что математика создала богатый арсенал методов, доказавших свою эффективность в разных отраслях знаний.
2. В соответствии с «Законом РФ «Об образовании» в деятельности учащихся на занятиях творческая сторона должна преобладать над практической. Использовать поисковый и исследовательский методы обучения.
ЗАДАЧИ КУРСА:
1. Познакомить учащихся с математической логикой.
2. Показать, что теория множеств, служит прочным фундаментом математизации разнообразных наук: экономики, биологии, лингвистики…
3. Сформировать понятие упорядоченных пар.
4. На конкретных примерах сформировать понятие функциональной зависимости и свойств функции.
ТЕМАТИЧЕСКИЙ ПЛАН КУРСА ДЛЯ 5-го класса
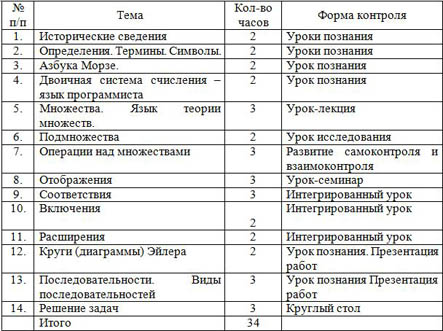
| № п/п | Тема | Кол-во часов | Форма контроля |
| 1. | Исторические сведения | 2 | Уроки познания |
| 2. | Определения. Термины. Символы. | 2 | Уроки познания |
| 3. | Азбука Морзе. | 2 | Урок познания |
| 4. | Двоичная система счисления – язык программиста | 2 | Урок познания |
| 5. | Множества. Язык теории множеств. | 3 | Урок-лекция |
| 6. | Подмножества | 2 | Урок исследования |
| 7. | Операции над множествами | 3 | Развитие самоконтроля и взаимоконтроля |
| 8. | Отображения | 3 | Урок-семинар |
| 9. | Соответствия | 3 | Интегрированный урок |
| 10. | Включения |
2 | Интегрированный урок |
| 11. | Расширения | 2 | Интегрированный урок |
| 12. | Круги (диаграммы) Эйлера | 2 | Урок познания. Презентация работ |
| 13. | Последовательности. Виды последовательностей | 3 | Урок познания Презентация работ |
| 14. | Решение задач | 3 | Круглый стол |
|
| Итого | 34 |
|
ТЕМАТИЧЕСКИЙ ПЛАН КУРСА 6-го класса
| № п/п | Тема | Кол-во часов | Форма контроля |
| 1. | Исторические сведения | 2 | Урок познания |
| 2. | Ряды. Последовательности | 3 | Урок исследования |
| 3. | Способы задания пос-ти | 3 | Интегрированный урок |
| 4. | Признак Коши. Признак Даламбера. | 3 | Интегрированный урок |
| 5. | Ряды Фурье | 3 | Урок исследования |
| 6. | Прогрессии | 4 | Презентация работ |
| 7. | Банковские расчеты | 4 | Интегрированный урок |
| 9. | Функциональные ряды | 3 | Поисково-исследовательский |
| 10 | Функциональные последовательности | 3 | Поисково-исследовательский |
| 8. | Представление о функции | 3 | Урок познания |
| 11. | Решение задач | 3 | Круглый стол |
|
| Итого | 34 |
|
ТЕМАТИЧЕСКИЙ ПЛАН КУРСА 7-го класса
| № п/п | Тема | Кол-во часов | Форма контроля |
| 1. | Исторические сведения | 2 | Урок познания |
| 2. | Функциональные зависимости | 3 | Поисково-исследовательский |
| 3. | Способы задания функций | 3 | Урок познания |
| 4. | Прямая и обратная зависимости | 3 | Исследовательский |
| 5. | Степенная функция | 3 | Исследовательский |
| 6. | Показательная функция | 6 | Исследовательский |
| 7. | Свойства функций | 4 | Урок познания |
| 8. | Бесконечно большие и бесконечно малые функции | 3 |
|
| 9. | Задачи на оптимизацию | 4 | Поисково-исследовательский |
| 10. | Математика, лишенная формул | 3 | Круглый стол |
|
| Итого | 34 |
|
СОДЕРЖАНИЕ ПРОГРАММЫ 5-го класса
1. Исторические сведения (2 часа)
Показать на конкретных примерах, что математические понятия – понятия отвлеченные, абстрактные, и они лишь слепок с реального мира. Что же такое математика? Что в ней самое главное? Что, прежде всего, характерно для любого из ее разделов, любой ее теории?
Люди с древности пытались отобразить мир символами: палочки, кружочки, фигурки зверей и птиц и т.д. Так возникли цифры – арабские, китайские, римские, даже числа племен майя и ацтеков.
2. Определения. Термины. Символы (2 часа)
Первый урок – это урок познания. Это урок вопросов и сомнений, озарений и открытий. В результате изучения темы учащимся будет несложно ответить, что такое определения, теоремы, аксиомы, что для краткости записи необходимы символы, а что бы нас понимали на другом конце земного шара, то нужны особые, математические термины.
3. Азбука Морзе (2 часа)
Итак, первый язык – язык радистов. Не секрет, что из точек и тире складываются буквы, а из букв – слова, из слов – фразы, из фраз – тексты, посылаемые в эфир.
4. Двоичная система счисления (2 часа)
Двоичная система счисления – язык программистов. Как записать любое число с помощью двух символов: 0 и 1? Перевод чисел из десятичной системы в двоичную систему, и обратно.
5. Множества (3 часа)
Человеческому мышлению свойственно трактовать то или иное собрание предметов, родственных по какому-либо признаку, как самостоятельный объект.
А, Б, В, Г, Д… - все вместе – алфавит.
1, 2, 3, 4, 5… - все вместе – натуральный ряд чисел.
Кофейник, молочник, сахарница, несколько чашек и блюдец. А все вместе – сервиз. Идея объединения проглядывается в каждом примере.
В современной математике понятие множества является одним из основных. Так или иначе, с него начинается изложение традиционных математических теорий, возникающих по мере расширения сферы применения математики.
Рассмотреть простейшие понятия и обозначения языка теории множеств. Который вот уже 100 лет составляет фундамент современного математического языка.
6. Подмножество (2 часа)
Элементы, образующие данное множество, можно объединять не сразу все вместе, а группируя их в разных комбинациях. Так можно получать различные подмножества данного множества.
7. Операции над множествами (3 часа)
Пересечения и объединения множеств – вот главные операции!
Вот классический пример из русской литературы, связанный с одновременным выполнением нескольких условий. В комедии Н.В. Гоголя «Женитьба» главная героиня, невеста Агафья Тихоновна, рассуждает так: «…если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять бы сколько-нибудь развязности, какая у Балтазара Балтазарыча, да, пожалуй. Прибавить к этому еще дородности Ивана Павловича – я бы тогда тотчас бы решилась…»
У четырех разных женихов есть разные свойства, и невеста мечтает о том, чтобы молодой человек обладал сразу всеми свойствами. С точки зрения множеств Агафья Тихоновна исследует вопрос о пересечении множеств.
Использование операции пересечения множеств в математике соответствует использованию союза «и» в русском языке, Родственный союз «или» связан с другой операцией над множествами – операцией объединения.
8. Отображения (3 часа)
Сформировать понятие отображения с помощью примеров.
1) Заселяется новый дом – устанавливается соответствие между жильцами и номерами квартир.
2) Идет экзамен, и каждому отвечающему ставится оценка: двойка, тройка, четверка, пятерка.
3) Представьте себе, что вы в другой стране. Вам надо как-то ориентироваться. Для этой цели придуманы информационные средства: медпункт – крест, камера хранения – чемодан, почта – конверт и т.д.
9. Соответствия (3 часа)
Рассматривается понятие упорядоченных пар, бинарное отношение. Например, разобраться в тонкостях родственных отношений. Брат моей жены – кто он мне? Деверь? Шурин? А кто токая свояченица?
Описанные отношения характеризуются числовыми парами (1,1), (1,2), (1,3) и т.д.
10. Включения (2 часа)
Если каждый элемент множества В является элементом множества А, то множество В включено в множество А. Данную операцию можно рассмотреть на геометрических фигурах.
11. Расширение множества (3 часа)
Если заглянуть в глубокое прошлое человечества, то можно предположить возникновение натуральных чисел, как чисел необходимых для подсчета собранного урожая, подсчета домашней птицы и скота и т.д., т.е. прибыли. Взятый в долг мешок пшеницы должен был обозначаться другим числом. Возникла историческая необходимость расширения множества натуральных чисел до целых.
12. Круги (диаграммы) Эйлера (2 часа)
Изображение множеств в виде плоских фигур очень удобно для наглядного объяснения различных операций над множествами. Эти множества изображают в виде некоторых кругов. Такие круги называют кругами Эйлера в честь великого швейцарского математика Леонардо Эйлера (1707 -1783).
13. Последовательности (3 часа)
Как по-честному разделить конфету? Конечно как в песне: тебе половину и мне половину. А если делить на большее количество, то, что получится?
14. Решение задач (3 часа)
Итоговое занятие можно посвятить презентациям учеников по различным темам курса «Математика в образах».
СОДЕРЖАНИЕ ПРОГРАММЫ 6-го класса
1. Исторические сведения (2 часа)
Как по-честному разделить конфету? Конечно как в песне: тебе половину и мне половину. А если делить на большее количество, то, что получится?
Одна четвертая, одна восьмая, одна шестнадцатая… От долей конфет незаметно переходим к числам.
2. Ряды. Последовательности (3 часа)
Классический пример из геометрии, в котором используется теорема Вейерштрасса. Начертим окружность, и будем последовательно вписывать в нее правильные многоугольники: 4-угольник, 8-угольник, 16зугольник и т.д. Последовательность площадей (периметров) этих многоугольников возрастает и ограничена: снизу числом 0, а сверху, например, числом, выражающим площадь (периметр) описанного около окружности квадрата. Значит, построенная последовательность сходится, ее предел принимается за площадь круга (за длину окружности). Именно с помощью таких рассуждений и получена формула площади круга и формула длины окружности.
Решение задачи Гаусса о нахождении суммы чисел от 1 до 100.
3. Способы задания последовательности (3часа)
Рассмотреть словесный, аналитический, рекуррентный способы задания последовательностей. Рассмотреть последовательность Фибоначчи: 1,1,2,3,5,8,13,21,34,55…
4. Признак Коши. Признак Даламбера (3 часа)
Если числа достаточно малы (дроби), то ряд сходится к единицы, а если велики, то расходится.
5. Ряды Фурье (3часа)
Многие явления природы протекают периодически, т.е. повторяются в определенном порядке по истечении некоторого промежутка времени, называемого в математике периодом. Возникает вопрос: Как описать такие явления с помощью математики?
Прогрессии (4часа)
Рассмотреть особые последовательности: арифметическая и геометрическая прогрессии.
7. Банковские расчеты (4 часа)
Представьте себе, что Вы открыли вклад в банке в некоторой сумме, под проценты на несколько лет. У Вас есть две стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, т.е. получать прибыль, либо прийти в банк один раз – в конце срока хранения вклада. Какой доход вы получите в том и другом случаях? Рассмотрение формулы простых процентов и формулы сложных процентов.
8. Представление о функции (3 часа)
С помощью нехитрых примеров продемонстрировать важное достоинство функциональной зависимости: проблема – «Человек и окружающая среда».
9. Функциональные ряды (3 часа)
10.Функциональные последовательности (3 часа)
11. Решение задач (3 часа)
Итоговое занятие можно посвятить презентациям учеников по различным темам курса «Математика в образах».
СОДЕРЖАНИЕ ПРОГРАММЫ 7-го класса
Исторические сведения (2 часа)
С помощью нехитрых примеров продемонстрировать важное достоинство функциональной зависимости: проблема – «Человек и окружающая среда».
Функциональные зависимости (3 часа)
Когда человек приходит устраиваться на новую работу часто можно слышать такие слова: «Ваши функциональные обязанности будут заключаться в следующем…» Или в медицинском кабинете: «У Вас функциональное расстройство кишечника». Итак, в чем же смысл функциональных зависимостей этих ситуаций и какова их связь с математикой? Изучая какой-либо реальный процесс. Обычно обращают внимание на две величины, участвующие в нем. Одна из них меняется как бы сама по себе, независимо ни от чего, а другая принимает значения, каждое из которых каким-то образом зависит от выбранного.
Способы задания функций (3 часа)
Задать функцию – это значит указать правило. Чаще всего правило записывают формулой или несколькими формулами. Это аналитический способ задания. А если на координатной плоскости задана какая-нибудь кривая, то говорят, что функция задана графическим способом. Так же существуют табличный и графический способы задания функции.
Прямая и обратная зависимости (3 часа)
Данная тема легко разбирается на житейских примерах.
Степенная функция (3 часа)
По свойствам данная функция частично совпадает с функцией обратной пропорциональности, но отображает более сложные процессы в математике.
6.Показательная функция (6 часов)
Данную функцию называют – экспонентой. Достаточно много реальных ситуаций, где данная функция используется, как математическая модель. Например, в физике известен закон радиоактивного распада вещества – период полураспада.
Предположим, что колония живых организмов находится в благоприятных условиях: пространство и пищевые ресурсы не ограничены, а хищников, питающихся данными организмами нет, благодаря чему рождаемость выше, чем смертность. С какой скоростью увеличивается колония? Закон показательного роста. Примерно по такому же закону изменяется величина вклада в банковской структуре.
В комнату с температурой 20 С внесли кипящий чайник. Как изменятся их температуры? Процессы подобного рода называют процессами выравнивания.
7.Свойства функций (4 часа)
Перечислить свойства функций. Данную тему можно рассмотреть в ходе проведения деловой игры. Функции – это математические портреты устойчивых закономерностей, познаваемых человеком
Проиллюстрировать характерные свойства функций можно на пословицах и поговорках, т.к. пословицы – это отражение устойчивых закономерностей, проверенных многовековым опытом народа.
«Чем дальше в лес, тем больше дров», «Кашу маслом не испортишь» и т.д. Построить графики каждого из высказываний.
8.Бесконечно большие и бесконечно малые функции (3 часа)
9.Задачи на оптимизацию (4 часа)
На практике всем нам часто приходится решать так называемые задачи на оптимизацию (optimum – наилучший). Инженеры-технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции; конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей; экономисты стараются спланировать связи завода с источником сырья так, чтобы транспортные расходы оказались минимальными, и т.д.
В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение второй величины, при котором первая принимает свое наименьшее или наибольшее значение.
10. Математика, лишенная формул (3 часа)
Итоговое занятие по знакомству с математикой, лишенной формул и строгих доказательств. Последнее занятие можно провести в форме круглого стола, предоставив возможность каждому из учащихся поделиться своими наработками по данной теме. Через все выступления красной нитью должна проходить мысль, что математика создала богатый арсенал методов, доказавших свою эффективность во всех сферах жизни человека, и во всех областях науки.
Список литературы
1.Калужин А.А. «Элементы теории множеств и математической логики в школьном курсе математики» - Москва, «Просвещение», 1978 г.
2.Эрдниев П.М. «Методика упражнений по математике» - Москва, «Просвещение», 1970 г.
3.Шуба М.Ю. «Занимательные задания в обучении математике». Книга для учителя. – Москва, «Просвещение», 1994 г.
4.Попов Ю.П. «Математика в образах» - Москва, «Знание», 1989 г.
5.Петраков И.С. «Математические кружки» - Москва, «Просвещение», 1987 г.
6.Пичурин Л.Ф. «Воспитание учащихся при обучении математике». Книга для учителя. – Москва, «Просвещение», 1987 г.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Факультативный курс "Математика в образах" (0.11 MB)
Факультативный курс "Математика в образах" (0.11 MB)
 0
0 681
681 39
39 Нравится
0
Нравится
0







