Педагогическая разработка
Адаптационная программа
факультативного курса по математике
для обучающихся 2 класса
«ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА»
Автор программы:
Бухарова Наталья Сергеевна
Учитель начальных классов
2012 г.
Содержание
Пояснительная записка 3
Описание разделов программы 7
Учебно-тематическое планирование 9
Требования к уровню усвоения курса 12
Список литературы 16
Приложение
Пояснительная записка.
Настоящая программа разработана на основе государственной программы факультативного курса «Занимательная математика» Е.Э.Кочуровой [1], авторской программы для начальной школы «Юным умникам и умницам. Развитие познавательных способностей» О.А.Холодовой [2], рекомендованной Министерством образования науки РФ. Программа курса составлена в соответствии с требованиями Концепции ФГОС второго поколения и предназначена для учащихся 2 класса[12].
Структура данной программы была разделена на 5 модулей. Занятия программы Е.Э.Кочуровой были объединены в модули «Занимательная геометрия» и «Очень важную науку постигаем мы без скуки». Следует заметить то, что не все занятия внесены в адаптационную программу, так как схожие занятия по целям и задачам с программой О.А.Холодовой, целесообразно было не дублировать. Как отмечают психологи (А.Г.Асмолов, Л.С.Выготский), большую роль в процессе учебной деятельности школьников начальных классов играет уровень познавательных процессов: внимание, память, мышление, восприятие. Поэтому в данной программе был внесен модуль «Развитие познавательных процессов», за основу которого взята программа О.А.Холодовой «Умники и умницы». Модули «Что дала математика людям? Зачем ее изучать» и «Из истории математики» были внесены в программу курса для расширения и углубления знаний программного материала, а также для знакомства с некоторыми общими идеями современной математики и применения этих знаний в жизни.
Актуальность программы факультативного курса «Занимательная математика».
Программа предусматривает включение задач и заданий, трудность которых определяется не столько математическим содержанием, сколько новизной и необычностью математической ситуации. Это способствует появлению желания отказаться от образца, проявить самостоятельность, формированию умений работать в условиях поиска, развитию сообразительности, любознательности. Предлагаемый факультатив разработан в соответствии ФГОС второго поколения и предназначен для развития математических способностей учащихся, для формирования элементов логической и алгоритмической грамотности, коммуникативных умений младших школьников с применением коллективных форм организации занятий и использованием современных средств обучения. Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности позволят обучающимся реализовать свои возможности, приобрести уверенность в своих силах.
Новизна программы состоит в том, что данный факультативный курс дополняет и расширяет математические знания, прививает интерес к предмету и позволяет использовать эти решения на практике, а также направлен на развитие познавательных процессов. Материал программы подобран и размещен в соответствии с тематикой модулей.
Значимость данного курса заключается в том, что изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений. Изучение математики развивает воображение, пространственные представления. История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Но также важно показать детям, что математика не только нужна в жизни, но еще и интересна.
Новая парадигма образования 21 века – вооружение школьников умениями самостоятельно учиться: приобретать знания, умения, навыки УУД, способы деятельности (познавательные, информационно-коммуникативные, рефлексивные).
На этой методологии основываются стандарты нового поколения для начальной и основной школы. Основой реализации стандартов нового поколения является системно-деятельностный подход. Программа занятий строится с учетом компонентов данного подхода:
мотивационный, на котором ставится учебная задача, с актуализацией ЗУН;
планирование и организация деятельности, здесь нужны учебные действия с созданием ситуации успеха, именно на этом этапе вырабатываются УУД;
самоконтроль и самооценка, такая последовательность необходима на любом системно - деятельностном уроке.
Цель курса: развитие математического образа мышления и устойчивого интереса к предмету «Математика».
Программа призвана способствовать решению следующих задач:
Формировать представления о математике как части общечеловеческой культуры.
Предоставить дополнительные возможности для развития творческих способностей учащихся.
Научить решать текстовые задачи (занимательного, исторического характера), работать с научной и справочной литературой, с измерительными инструментами.
Закрепить навыки устных и письменных вычислений.
Создать условия для формирования и поддержания устойчивого интереса к математике.
Воспитывать ответственность, усидчивость, целеустремлённость, способность к взаимопомощи и сотрудничеству.
Программа факультатива рассчитана на год. Занятия проводятся 1 раз в неделю. Продолжительность каждого занятия не превышает 30-40 минут. Всего 34 часа в течение года.
Работа факультативного курса строится на принципах:
Регулярности – еженедельно;
Параллельности – 1) проведение факультативных занятий в значительной степени близко к урокам. Сходство занятий определяется организационной формой коллективной учебной работы, когда учитель ведет занятие с группой учащихся, проводит необходимые пояснения, спрашивает учащихся. При этом целесообразно учащимся предоставлять собственные суждения по обсуждаемому вопросу. 2) связь с учебным материалом, так как без занимательных задач преподавание не бывает успешным, поскольку занимательность повышает интерес к предмету и способствует осмыслению важной идеи: математика окружает нас, она везде. Систематичность изложения материала должна быть направлена на общее умственное развитие учащихся.
Самостоятельности – значительная часть практического материала выполняется учащимися самостоятельно.
Вариативности и самоконтроля – набор задач различного уровня сложности и проверка решений по образцу, алгоритму, ключу.
При проведении занятий применяются личностно-ориентированные технологии обучения, такие как:
1) технология полного усвоения знаний, когда все обучаемые способны полностью усвоить необходимый учебный материал при рациональной организации учебного процесса;
2) технология разноуровневого обучения или «технология обучения базису без отстающих»;
3) технология коллективного взаимообучения, которая позволяет плодотворно развивать у обучаемых самостоятельность и коммуникативные умения.
В процессе выполнения заданий дети учатся видеть сходства и различия, замечать изменения, выявлять причины и характер этих изменений, на этой основе формулировать выводы. Совместное с учителем движение от вопроса к ответу – это возможность научить ученика рассуждать, сомневаться, задумываться, стараться и самому найти выход – ответ.
Программа учитывает возрастные особенности младших школьников и поэтому предусматривает организацию подвижной деятельности учащихся, которая не мешает умственной работе. С этой целью включены подвижные математические игры, предусмотрена последовательная смена учеником «центров» деятельности в течение одного занятия; передвижения по классу в ходе выполнения математических заданий на листах бумаги, расположенных на стенах классной комнаты и др. Во время занятий важно поддерживать прямое общение между детьми (возможность подходить друг к другу, переговариваться, обмениваться мыслями). При организации занятий целесообразно использовать принцип игр «Ручеек», «Пересадки», принцип свободного перемещения по классу, работу в парах постоянного и сменного состава, работу в группах, некоторые математические игры и задания могут принимать форму состязаний, соревнований между командами («Веселый счет», «Математическое путешествие» и др.)
Дополнительные занятия по математике, предусмотренные данной программой, носят, прежде всего, не оценочный, а обучающий и развивающий характер. Программа рассчитана на работу с учащимися вторых классов, что отражается на приоритете учебных задач, возникающих в ходе проведении занятий. Во втором классе много внимания уделяется самостоятельной деятельности учеников, равно как и их навыкам самоконтроля; кроме того, второклассникам предлагается значительный объём разнообразных нестандартных текстовых задач. Это связано с необходимостью их подготовки к участию в математических конкурсах и олимпиадах. Кроме того, учебная программа второго класса по математике предполагает формирование большого количества различных вычислительных навыков. Это рутинная, но необходимая работа, и занятия данной программы позволяют вносить разнообразие в математическое образование второклассников, поскольку содержат большое количество игр и занимательных заданий.
Факультативные занятия построены так, чтобы быть для учащихся интересными, увлекательными и занимательными. Умело использовать естественную любознательность школьников для формирования устойчивого интереса к математике. Занимательность помогает учащимся освоить факультативный курс, содержащиеся в нем идеи и методы математической науки, логику и приемы творческой деятельности.
Учащимся, увлеченным математикой, мало тех знаний, которые они получают на уроках математики. Они хотят знать о прикладной ее стороне, решать более сложные задачи.
Методика проведения занятий основана на создании обучающей ситуации, в которой математические идеи и факты вырабатываются самими школьниками в процессе решения разнообразных задач.
В приложении представлены примеры занятий, а также виды заданий.
Формы подведения итогов реализации программы
Итоговый контроль осуществляется в формах:
- тестирование;
- практические работы;
- творческие работы учащихся;
- контрольные задания.
Самооценка и самоконтроль определение учеником границ своего «знания - незнания», своих потенциальных возможностей, а также осознание тех проблем, которые ещё предстоит решить в ходе осуществления деятельности.
Содержательный контроль и оценка результатов учащихся предусматривает выявление индивидуальной динамики качества усвоения предмета ребёнком и не допускает сравнения его с другими детьми.
Результаты проверки фиксируются в зачётном листе учителя. В рамках накопительной системы, создание портфолио и отражаются в индивидуальном образовательном маршруте (Приложение 15).
Описание разделов программы
Каждое занятие наполнено богатым историческим материалом, энциклопедическими сведениями в математических заданиях. Задания с природоведческим и историческим сюжетом позволяют детям увидеть неразрывную связь математики с окружающим миром, расширяют их кругозор, обогащают активный словарный запас.
В процессе проведения занятий решается проблема дифференциации обучения, расширяются рамки учебной программы, появляется реальная возможность, работая в зоне ближайшего развития каждого ребенка, поднять авторитет даже самого слабого ученика. В зависимости от целей конкретного урока и специфики темы формы занятий могут быть различны:
уроки - исследования,
ролевые игры,
уроки - путешествия,
уроки –праздники.
Основные виды деятельности учащихся:
решение занимательных и игровых задач;
оформление математических газет;
знакомство с научно-популярной литературой, связанной с математикой;
проектная деятельность
самостоятельная работа;
работа в парах, в группах;
творческие работы.
Основное содержание программы
Модуль 1. Что дала математика людям? Зачем её изучать? – 2ч
Математика вокруг нас. Логическая последовательность. Родственные ряды. Волшебные звёзды. Поиск лишнего ряда. Числовые головоломки: соединение чисел знаками действия так, чтобы в ответе получилось заданное число и др. Поиск нескольких решений.
Восстановление примеров: поиск цифры, которая скрыта. Последовательное
выполнение арифметических действий: отгадывание задуманных чисел.
Модуль 2. Из истории математики - 5ч
История возникновения счета числами, запись числа у разных народов древности, римская нумерация, магия числа – 5. Занимательные задания с римскими цифрами.
Модуль 3. Развитие познавательных способностей – 16ч
Игры на развитие познавательных процессов, мозговая гимнастика, решение творческо-поисковых и творческих задач, коррегирующая гимнастика для глаз, логические задачи на развитие аналитических способностей и способности рассуждать.
Модуль 4. Занимательная геометрия - 7 ч
Геометрические узоры. Закономерности в узорах. Симметрия. Фигуры,
имеющие одну и несколько осей симметрии. Расположение деталей фигуры в исходной конструкции. Части фигуры. Место заданной фигуры в конструкции.
Расположение деталей. Выбор деталей в соответствии с заданным контуром
конструкции. Поиск нескольких возможных вариантов решения. Составление и
зарисовка фигур по собственному замыслу. Разрезание и составление фигур. Деление заданной фигуры на равные по площади части. Поиск заданных фигур в фигурах сложной конфигурации. Решение задач, формирующих геометрическую наблюдательность. Распознавание (нахождение) окружности на орнаменте. Составление (вычерчивание) орнамента с использованием циркуля (по образцу, по собственному замыслу).
Модуль 5. Очень важную науку постигаем мы без скуки – 4ч
Головоломки с цифрами, числовые ребусы, магические квадраты, загадки с использованием чисел, логические задачи, сочинение. «Веселый счёт» – игра-соревнование; игры с игральными кубиками. Игры «Чья сумма больше?», «Лучший лодочник», «Русское лото», «Математическое домино», «Не собьюсь!», «Задумай число», «Отгадай задуманное число», «Отгадай число и месяц рождения». Игры «Волшебная палочка», «Лучший счётчик», «Не подведи друга», «День и ночь», «Счастливый случай», «Сбор плодов», «Гонки с зонтиками», «Магазин», «Какой ряд дружнее?». Игры с мячом: «Наоборот», «Не урони мяч».
Учебно-тематическое планирование
| №
| Содержание (модули, темы) | Кол-во Часов | Виды деятельности | Форма контроля |
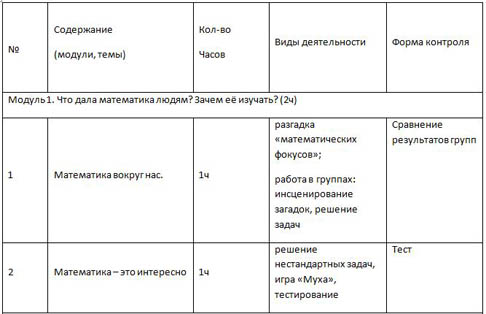
| Модуль 1. Что дала математика людям? Зачем её изучать? (2ч) |
| 1 | Математика вокруг нас. | 1ч | разгадка «математических фокусов»; работа в группах: инсценирование загадок, решение задач | Сравнение результатов групп |
| 2 | Математика – это интересно | 1ч | решение нестандартных задач, игра «Муха», тестирование | Тест |
| Модуль 2. Из истории математики. (5ч) |
| 1 | Из истории чисел и цифр. Как люди учились считать. Презентация «Как люди научились считать» | 1ч | работа со словарями, энциклопедиями; выполнение заданий презентации | Сравнение результатов групп |
| 2 | Удивительное рядом или старинные меры длины. | 1ч | работа со словарями, энциклопедиями | викторина |
| 3 | Из истории математических открытий. Архимед – гений математики и изобретений.
| 1ч | работа с энциклопедиями и справочной литературой
| Сравнение результатов групп |
| 4 | Научный мир Пифагора. Презентация «Знакомьтесь: Пифагор!» | 1ч | работа с информацией презентации | Проект - математическая газета «Великие математики» |
| 5 | Танграм – древняя китайская головоломка. | 1ч | составление картинки с заданным разбиением на части; с частично заданным разбиением на части; без заданного разбиения. | демонстрация выполненных работ |
| Модуль 3. Развитие познавательных способностей. (16ч) |
| 1 | Диагностика уровня РПС | 1ч | выполнение заданий диагностируемых уровень РПС | карта уровня развития РПС |
| 2-3 | Развитие концентрации внимания.
| 2ч | решение логических упражнений и задач. | проверка выполненной работы |
| 4-5 | Тренировка внимания.
| 2ч | работа в парах по решению задач; схематическое изображение задач | проект «Математический ребус» |
| 6-7 | Тренировка слуховой памяти |
2ч | работа в парах; устный счёт | проверка выполненной работы |
| 8-9 | Тренировка зрительной памяти | 2ч | решение задач повышенной сложности | проверка выполненной работы |
| 10-11 | Поиск закономерностей | 2ч | индивидуальная работа; решение нестандартных задач | проверка выполненной работы |
| 12-13 | Совершенствование воображения | 2ч | инсценирование задач | конкурс на лучшее инсценирование математической задачи |
| 14-15 | Развитие быстроты реакций | 2ч | работа в группах | Сравнение результатов групп |
| 16 | Конкурс эрудитов | 1ч | выполнение заданий диагностируемых уровень РПС | карта уровня РПС (итоговое) |
| Модуль 4. Занимательная геометрия. (7ч) |
| 1 | Занимательная геометрия. Презентация «Узоры геометрии» | 1ч | создание мини-альбома «Узоры геометрии» | выставка альбомов «Узоры геометрии» |
| 2 | Волшебная линейка | 1ч | изучение шкалы линейки, сведения из истории математики, работа в парах | Сравнение результатов |
| 3-4 | Конструирование многоугольников из деталей танграма | 2ч | составление многоугольников с заданным разбиением на части; с частично заданным разбиением на части; без заданного разбиения. | проверка выполненной работы |
| 5 | Прятки с фигурами | 1ч | поиск заданных фигур в фигурах сложных конфигурациях, работа в парах | взаимопроверка |
| 6 | Веселая геометрия | 1ч | решение задач, формирующих геометричекую наблюдательность | проверка выполненной работы |
|
7 |
Турнир по геометрии
|
1ч | запись геометрических понятий, решение геометрических заданий | проверка выполненной работы |
| Модуль 5. Очень важную науку постигаем мы без скуки. (4ч) |
| 1 | Математическая карусель | 1ч | работа в «центрах» деятельности «Танграм», «Математические головоломки», «Занимательные задачи», работа в малых группах | Сравнение результатов групп |
| 2 | Игра-соревнование «Веселый счет» | 1ч | решение игровых заданий
| проверка выполненной работы |
| 3 | Познавательная конкурсно-игровая программа «В гостях у Царицы Математики» Презентация. | 1ч | решение игровых заданий | Сравнение результатов групп |
| 4 | Сочинение «Место математики в моей жизни». | 1ч | творческая работа | выставка рисунков «Математика вокруг нас» |
|
| Всего | 34 |
|
|
|
|
|
|
|
|
Материально-техническая база
Справочно-энциклопедическая литература.
Детские книги разных типов из круга детского чтения.
Компьютер.
Мультимедийное оборудование.
Слайды. Презентации.
Требования к уровню усвоения курса
Учащиеся, посещающие факультатив, в конце учебного года могут научиться:
находить наиболее рациональные способы решения логических задач, используя при решении таблицы и «графы»;
оценивать логическую правильность рассуждений;
распознавать плоские геометрические фигуры, уметь применять их свойства при решении различных задач;
решать простейшие комбинаторные задачи путём систематического перебора возможных вариантов;
уметь составлять занимательные задачи;
применять некоторые приёмы быстрых устных вычислений при решении задач;
применять полученные знания при построении геометрических фигур и использованием линейки и циркуля.
Сформированные действия
В ходе реализации программы у младших школьников могут быть сформированы следующие способности:
Рефлексировать (видеть проблему; анализировать сделанное – почему получилось, почему не получилось, видеть трудности, ошибки);
Целеполагать (ставить и удерживать цели);
Планировать (составлять план своей деятельности);
Моделировать (представлять способ действия в виде модели-схемы, выделяя все существенное и главное);
Проявлять инициативу при поиске способа (способов) решения задачи;
Вступать в коммуникацию (взаимодействовать при решении задачи, отстаивать свою позицию, принимать или аргументировано отклонять точки зрения других).
Ожидаемые результаты и способы их проверки
Личностными результатами изучения курса является формирование следующих умений:
- Определять и высказывать под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы).
- В предложенных педагогом ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, при поддержке других участников группы и педагога, как поступить.
Для оценки формирования и развития личностных характеристик воспитанников (ценности, интересы, склонности, уровень притязаний положение ребенка в объединении, деловые качества воспитанника) используется
Межпредметными результатами изучения курса во 2-м классе являются связи:
с уроками изобразительного искусства: оформление творческих работ, участие в выставках рисунков при защите проектов;
Для отслеживания уровня усвоения программы и своевременного внесения коррекции целесообразно использовать следующие формы контроля:
занятия-конкурсы на повторение практических умений,
занятия на повторение и обобщение (после прохождения основных разделов программы),
самопрезентация (просмотр работ с их одновременной защитой ребенком),
участие в математических олимпиадах и конкурсах различного уровня.
Кроме того, необходимо систематическое наблюдение за воспитанниками в течение учебного года, включающее:
результативность и самостоятельную деятельность ребенка,
активность,
аккуратность,
творческий подход к знаниям,
степень самостоятельности в их решении и выполнении и т.д.
Предметными результатами изучения курса являются формирование следующих умений.
- описывать признаки предметов и узнавать предметы по их признакам;
- выделять существенные признаки предметов;
- сравнивать между собой предметы, явления;
- обобщать, делать несложные выводы;
- классифицировать явления, предметы;
- определять последовательность событий;
- судить о противоположных явлениях;
- давать определения тем или иным понятиям;
- определять отношения между предметами типа «род» - «вид»;
- выявлять функциональные отношения между понятиями;
- выявлять закономерности и проводить аналогии.
Проверка результатов проходит в форме:
игровых занятий на повторение теоретических понятий (конкурсы, викторины, составление кроссвордов и др.),
собеседования (индивидуальное и групповое),
опросников,
тестирования,
проведения самостоятельных работ репродуктивного характера и др. [9]
Метапредметные результаты:
Определять цель деятельности на уроке с помощью учителя и самостоятельно.
Учиться совместно с учителем обнаруживать и формулировать учебную проблему совместно с учителем.
Учиться планировать учебную деятельность на уроке.
Высказывать свою версию, пытаться предлагать способ её проверки (на основе продуктивных заданий ).
Работая по предложенному плану, использовать необходимые средства (учебник, простейшие приборы и инструменты).
Средством формирования этих действий служит технология проблемного диалога на этапе изучения нового материала.
Для оценки эффективности занятий по РПС можно использовать следующие показатели:
степень помощи, которую оказывает взрослый учащимся при выполнении заданий: чем помощь взрослого меньше, тем выше самостоятельность учеников и, следовательно, выше развивающий эффект занятий;
поведение учащихся на занятиях: живость, активность, заинтересованность школьников обеспечивают положительные результаты занятий;
результаты выполнения тестовых заданий и заданий из конкурса эрудитов, при выполнении которых выявляется, справляются ли ученики с этими заданиями самостоятельно;
косвенным показателем эффективности данных занятий может быть повышение успеваемости по разным школьным дисциплинам, а также наблюдения учителей за работой учащихся на других уроках (повышение активности, работоспособности, внимательности, улучшение мыслительной деятельности).
Занятия рассчитаны на групповую и индивидуальную работу. Они построены таким образом, что один вид деятельности сменяется другим. Это позволяет сделать работу динамичной, насыщенной и менее утомительной, при этом принимать во внимание способности каждого ученика в отдельности, включая его по мере возможности в групповую работу, моделировать и воспроизводить ситуации, трудные для ученика, но возможные в обыденной жизни; их анализ и проигрывание могут стать основой для позитивных сдвигов в развитии личности ребёнка.
Список литературы для учителя:
Кочурова Е.Э. Программа факультативного курса «Занимательная математика». М.: Росткнига, 2010.
Холодова О.А. «Юным умникам и умницам: Задания по развитию познавательных способностей 7-8 лет (2 класс). Курс «РПС». М.: Росткнига, 2004.
Холодова О. Юным умникам и умницам: Задания по развитию познавательных способностей (7-8 лет). - Методическое пособие, 2 класс. Курс «РПС». М.: Росткнига, 2008 .
Дик Н. Ф. 1000 олимпиадных заданий по математике в начальной школе: учебное пособие. – Ростов-на-Дону: Феникс, 2010.
Список дополнительной литературы для учителя:
Агаркова Н. В. Нескучная математика. 1 – 4 классы. Занимательная математика. Волгоград: Учитель, 2007.
Асарина Е. Ю., Фрид М. Е. Секреты квадрата и кубика. М.: Контекст, 1995.
Агафонова И. Учимся думать. Занимательные логические задачи, тесты и упражнения для детей 8 – 11 лет. СПб,: МиМ-Экспресс1996.
Лавриненко Т. А. Задания развивающего характера по математике. Саратов: Лицей, 2002.
Методика работы с задачами повышенной трудности в начальной школе. М.: Панорама, 2006.
«Начальная школа» Ежемесячный научно-методический журнал
Сахаров И. П. Аменицын Н. Н. Забавная арифметика. СПб.: Лань, 1995.
Симановский А. Э. Развитие творческого мышления детей. М.: Академкнига/Учебник, 2002.
Стандарты второго поколения. Оценка достижения планируемых результаов в начальной школе.Ч.1 – М.: Просвещение, 2010.
Сухин И. Г. Занимательные материалы. М.: Вако, 2004.
Узорова О. В., Нефёдова Е. А. «Вся математика с контрольными вопросами и великолепными игровыми задачами. 1 – 4 классы. М.: АСТ, 2004.
Федеральный государственный образовательный стандарт начального общего образования – М.: Просвещение, 2011.
Шкляров Т. В. Как научить вашего ребёнка решать задачи. М.: Грамотей, 2004.
Список литературы для учащихся:
Вахновецкий Б.А. Логическая математика для младших школьников. М.: Новый учебник, 2002.
Зак А. 500 занимательных логических задач для школьников. М.: Юнвес, 2002.
Левитас Г.Г. Нестандартные задачи 1-4 классы. М.: Илекса, 2002.
Лихтарников Л.М. Числовые ребусы. СПб.: Лань, Мик, 1996.
Савин А.П. Математические миниатюры. М.: Детская литература, 1998.
Сборник. Логические игры и задачи на уроках математики. Ярославль: Академия развития, 1997.
Сборник. Занимательные задачи для маленьких. М.: Омега, 1994.
Труднев В. Считай, смекай, отгадывай. СПб.: Лань, Мик, 1996.
Холодова О. Юным умникам и умницам. Рабочая тетрадь. М.: Росткнига, 2011.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Адаптационная программа "Занимательная математика" (2 класс) (59.44 КB)
Адаптационная программа "Занимательная математика" (2 класс) (59.44 КB)
 1
1 2429
2429 422
422 Нравится
0
Нравится
0


