Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Джордж Буль
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Пример:
« Трава зеленая » -истинное высказывание.
« Лев – птица » - ложное высказывание.
Не всякое предложение является логическим высказыванием. Пример: «ученик десятого класса» «информатика — интересный предмет».
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, н азываются составными. Высказывания, не являющиеся составными, называются элементарными .
Пример:
Элементарные высказывания:
« Петров — врач »,
« Петров — шахматист »
Составные высказывания:
- " Петров — врач и шахматист ", понимаемое как " Петров — врач, хорошо играющий в шахматы ".
- " Петров — врач или шахматист ", понимаемое в алгебре логики как " Петров или врач, или шахматист, или и врач и шахматист одновременно ".
Чтобы обращаться к логическим высказываниям, их обозначают буквами.
Пример:
А = «Луна – спутник Земли», А = 1
В = « 3* 2 = 5», В = 0
Пример:
А = "Тимур поедет летом на море",
В = "Тимур летом отправится в горы".
А и В = "Тимур летом побывает и на море, и в горах»
Операции над логическими
высказываниями
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логическое « отрицание »
( инверсия или НЕ) обозначается чертой над высказыванием Ā .
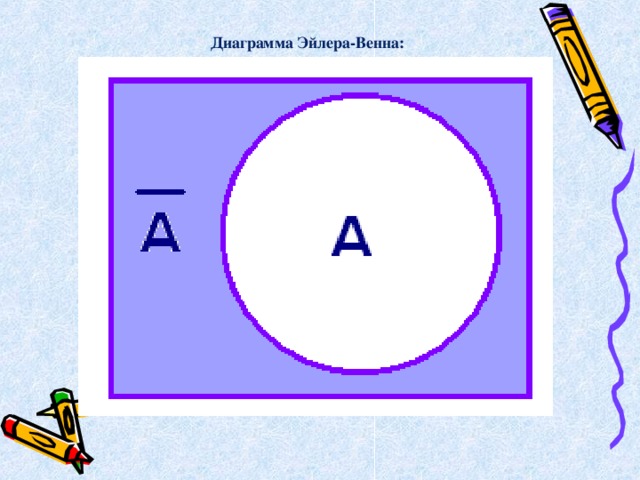
Диаграмма Эйлера-Венна:
Пример:
А = « Луна — спутник Земли »
А = " Луна — не спутник Земли "
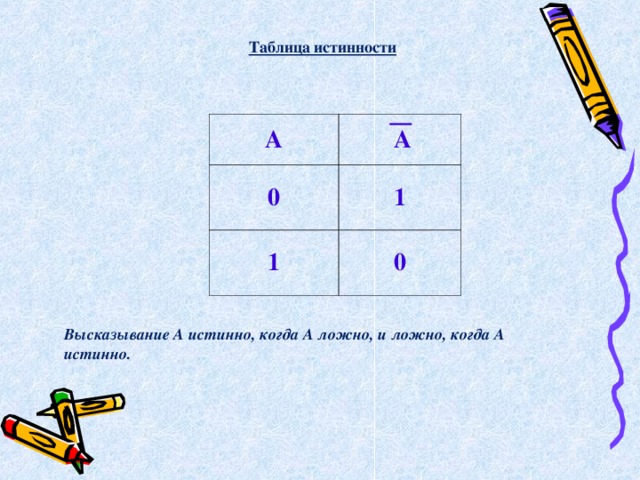
Таблица истинности
А
А
0
1
1
0
Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Логическое умножение
( « и », конъюнкция (лат. conjunctio — соединение)) обозначается точкой " . " (может также обозначаться знаками /\ или & ).
А . В, А /\ В, А & В
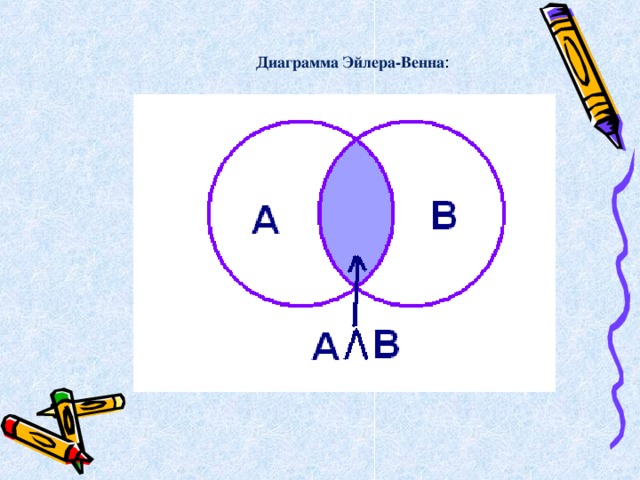
Диаграмма Эйлера-Венна
Пример:
А = «10 делится на 2», А= 1
В = «5 больше 3», В = 1
С = « 4 – нечётное число», С = 0
А & В = «10 делится на 2 и 5 больше 3», А & В = 1
А & С = « 10 делится на 2 и 4 – чётное число», А & С = 0
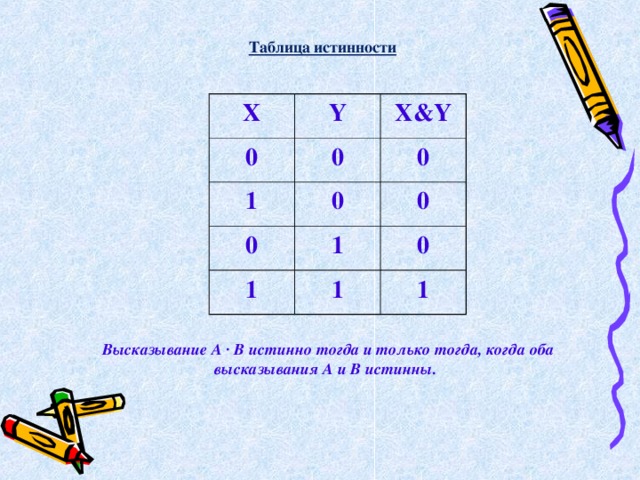
Таблица истинности
X
Y
0
1
X&Y
0
0
0
0
0
1
1
1
0
1
Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Логическое сложение
( « или » , дизъюнкция (лат. disjunctio — разделение) обозначается знаком v или + .
А V В, А + В
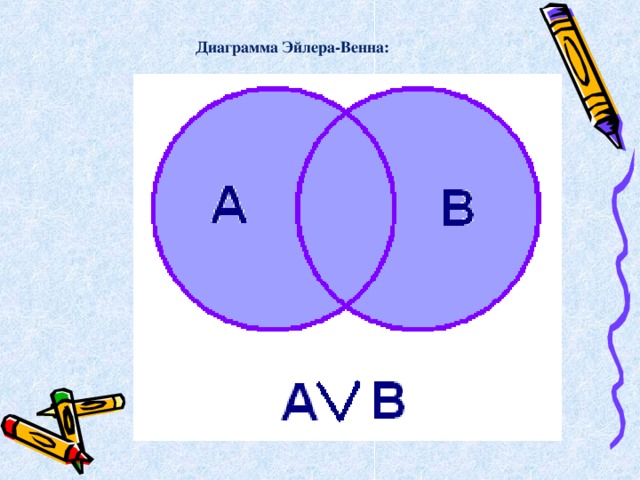
Диаграмма Эйлера-Венна:
Таблица истинности
X
Y
0
X + Y
0
1
0
0
0
1
1
1
1
1
1
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Импликация (лат. implico — тесно связаны)
-операция, выражаемая связками «если ..., то…», «из ... следует…», «... влечет ...».
Обозначается знаком .
А В
.
Таблица истинности
А
В
0
А В
0
0
1
1
0
1
0
1
1
1
1
Высказывание А В ложно тогда и только тогда, когда А истинно, а В – ложно.
Эквиваленция (двойная импликация)
- операция, выражаемая связками « тогда и только тогда », « необходимо и достаточно », «... равносильно ...» Обозначается знаком или ~.
А В, А ~ В.
Таблица истинности
А
В
0
0
А В
0
1
1
1
0
0
1
1
0
1
- Высказывание А В истинно тогда и только тогда, когда значения А и В совпадают.
Пример:
А = «10 делится на 2», А= 1
В = «5 больше 3», В = 1
С = « 4 – нечётное число», С = 0
К = « 3 – чётное число», К = 0
А + В = «10 делится на 2 или 5 больше 3», А + В = 1
А + С = « 10 делится на 2 или 4 – чётное число», А + С = 1
С + К = « 4 – нечётное число или 3 – чётное число», С+К = 0
Порядок выполнения логических операций
1 .Сначала выполняется операция отрицания (“не”),
2. Затем конъюнкция (“и”),
3. После конъюнкции — дизъюнкция (“или”),
4. В последнюю очередь — импликация и эквиваленция.
¬B " width="640"
Законы логики.
- A → B = ¬ A B
- Законы де Моргана ¬ (A B) = ¬ A ¬ B
¬ (A B) = ¬ A ¬ B
3. Законы коммутативности А &B B&A
AVB BVA
4. Законы ассоциативности ( А &B)&C A&(B&C)
( А VB)VC AV(BVC)
5. Законы дистрибутивности А & ( BVC) (A&B)V(A&C)
А V ( B&C) (AVB)&(AVC)
6. Законы поглощения A&(AVB) A
AV(A&B) A
7. Законы противоречия A&¬A=0
8. Закон исключения третьего AV¬A=1
9. Закон двойного отрицания ¬¬A=A
10. Закон контрапозиции A-›B ¬A - ¬B
Получите свидетельство
Вход
Основы логики (презентация) (0.46 MB)
0
648
74
Нравится
0
