Основы логики. Таблицы истиности

Основы логики.

Таблицы истинности.

Законы алгебры логики.

Задачи, решаемые с использованием таблиц истинности

АЛГЕБРА ЛОГИКИ

Алгебра логики – это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

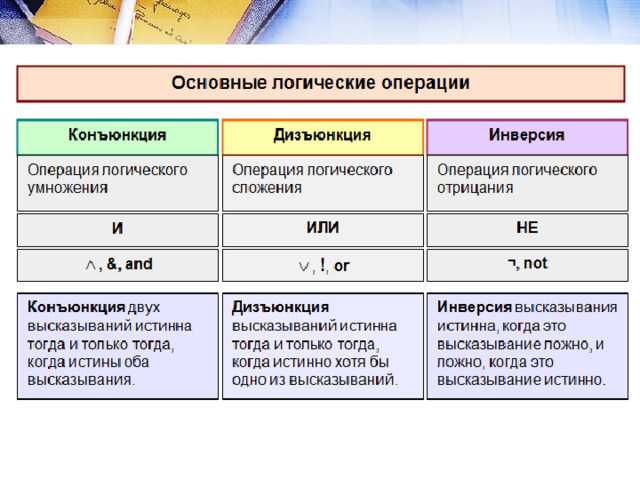
В алгебре логики изучаются логические операции, производимые над высказываниями.

ПРИМЕР ПРОСТЫХ ВЫСКАЗЫВАНИЙ

• На улице идет дождь.
• На улице светит солнце.
• На улице пасмурная погода.
• На улице идет снег.

ПРИМЕР СЛОЖНОГО ВЫСКАЗЫВАНИЯ

“ Тимур поедет летом на море” – высказывание А,

“ Тимур летом отправится в горы”- высказывание B.

Тогда составное высказывание “обозначаемые, соответственно, “1” и “0”.

ЗАКРЕПЛЕНИЕ

• 2*2=4.
• Волга впадает в черное море.
• Книга-источник знаний.
• Сейчас месяц апрель.
• Идет урок информатики.
• 16-8=9

истина

ложь

истина

истина

истина

ложь

ОБОЗНАЧЕНИЕ ВЫСКАЗЫВАНИЯ

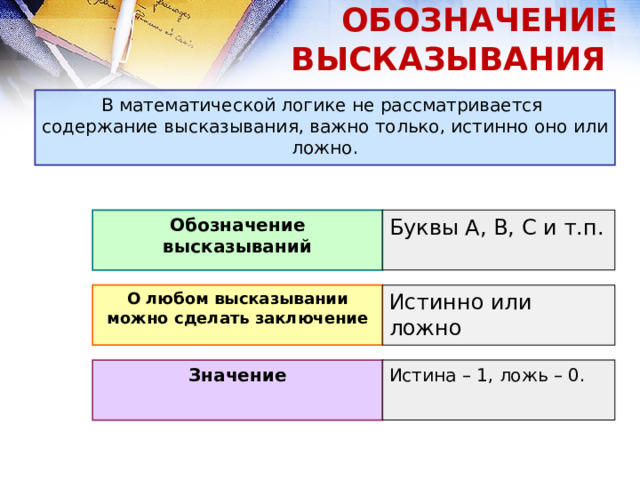
В математической логике не рассматривается содержание высказывания, важно только, истинно оно или ложно.

Обозначение высказываний

Буквы A, B, C и т.п.

О любом высказывании можно сделать заключение

Истинно или ложно

Значение

Истина – 1, ложь – 0.

ПРИМЕР

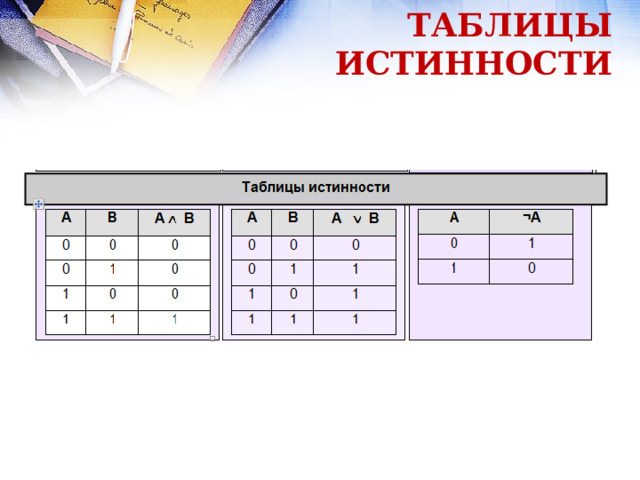
ТАБЛИЦЫ ИСТИННОСТИ

ПРИМЕР

ОБЩЕЕ ПРАВИЛО ПОСТРОЕНИЯ ТАБЛИЦ ИСТИННОСТИ

ОБЩЕЕ ПРАВИЛО ПОСТРОЕНИЯ ТАБЛИЦ ИСТИННОСТИ

ОБЩЕЕ ПРАВИЛО ПОСТРОЕНИЯ ТАБЛИЦ ИСТИННОСТИ

ОБЩЕЕ ПРАВИЛО ПОСТРОЕНИЯ ТАБЛИЦ ИСТИННОСТИ

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

• Выражение в скобках
• Логическое НЕ
• Логическое И (конъюнкция)

• Л огическое ИЛИ (дизъюнкция)

ПРИМЕР

F=  A  B

N=2

Количество переменных -

Q=2 2 =4

Количество строк в таблице- Q=2 N

F=  A  B

Количество операций и их последовательность

К=2

1

2

4

Количество столбцов в таблице- К+N

A

B

1

2

1

1

0

1

1

0

0

0

0

0

1

1

1

1

0

1