Основное свойство рациональной дроби
7 класс
Цели:
Формировать умение сокращать дроби и приводить дроби к новому знаменателю
Способствовать формированию познавательной активности, умению логически мыслить, рационально работать.
Воспитательные цели:
Формирование чувства ответственности;
Воспитание аккуратности, усидчивости, прилежности;
Привитие интереса к изучаемому предмету;
Воспитание обязательного отношения к обучению.
Развивающие цели:
Формирование умения выделять главное;
Развитие логического мышления;
Развитие мыслительной деятельности.
Используемые технологии:
Игровая технология;
Здоровьесберегающая технология.
Тип урока: обобщение знаний
Оборудование: плакат для рефлексии, шпаргалки.
Ход урока
1.Организационный момент.
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
В алгебры мир отправимся смело,
В мир примеров и разных задач.
2.Мотивация урока.
А Эпиграфом урока буду слова греческого философа и математика Пифагора, жившего 500 л. до н. э. «Не делай никогда того, чего не знаешь, но научись всему, что нужно знать».
Я рада приветствовать вас на уроке математики. Вы должны сами угадать тему урока.
Подсказка - ребус.
 (дробь)
(дробь)
2)Какой вид дроби сейчас изучаете? (рациональную дробь)
Сегодня, продолжаем работать над темой «Основное свойство рациональной дроби». На уроке закрепим знания в сокращении дробей и научимся приводить рациональные дроби к новому знаменателю.
3. Актуализация знаний. Игра "ЧТО ЭТО ТАКОЕ?"
1)Выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля. (Целые выражение)
2) Целые и дробные выражения (Рациональные выражения)
3) Значения переменных, при которых выражение имеет смысл. (Допустимые значения переменных - ОДЗ)
4) Дробь, числителем и знаменателем которой являются многочлены. (Рациональная дробь)
5) Если числитель и знаменатель некоторой рациональной дроби умножить на один и тот же многочлен, не равный нулю, то получится дробь, равная исходной. (Основное свойство дроби)
6) Деление числителя и знаменателя дроби на одно и то же число, многочлен (Сокращение дроби)
4.Устная работа.
а) Определите какие из выражений являются целыми, какие дробными. Распределите по группам.
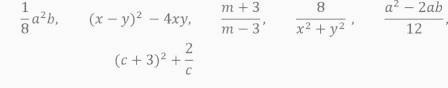
б) Ответьте на вопросы.
![]()
1) Найдите значение переменной, при которой дробь равна нулю.
2) Найдите значение переменной, при которой дробь не имеет смысла.
3) Найдите допустимые значения переменной для дроби.
в) Какие способы сокращение дробей вы знаете? (шпаргалка №1)
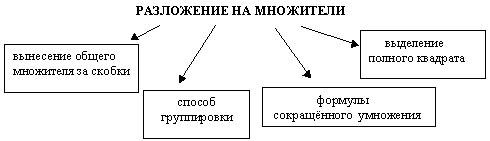
5.Закрепление
1)Укажите общий множитель числителя и знаменателя и сократите дробь. И узнаете имя великого древнего математика, который первый ввел обозначения для переменных.
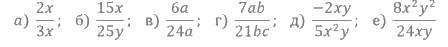
ё) 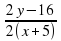
| 7b | х | 6а | 8ху | 5 | ху | 2 |
| ф | д | о | н | и | а | т |
- Вы получили имя ДИОФАНТ. Чем же знаменит он? Почему именно его имя я зашифровала в таблице?
ИСТОРИЧЕСКАЯ СПРАВКА (сообщение ученика)
Диофант Александрийский – один из величайших древнегреческих математиков, живший предположительно в III веке и заслуженно считающийся «отцом алгебры». Основное произведение Диофанта - Арифметика в 13 книгах. К сожалению, сохранились только 6 первых книг из 13. В сохранившихся книгах Диофанта содержится 189 задач с решениями. В пяти книгах содержатся методы решения неопределенных уравнений. Первая книга начинается с обширного введения, в котором описаны используемые Диофантом обозначения. Неизвестную Диофант называет "числом" и обозначает буквой ς, квадрат неизвестной - символом ∆γ "степень". Предусмотрены специальные знаки для следующих степеней неизвестного, вплоть до шестой, называемой кубо - кубом, и для противоположных им степеней. Знака сложения у Диофанта нет: он просто пишет рядом положительные члены, причём в каждом члене сначала записывается степень неизвестного, а затем численный коэффициент. Вычитаемые члены также записываются рядом, а перед всей их группой ставится специальный знак в виде перевёрнутой буквы Ш. Знак равенства обозначается двумя буквами ﺎ "равный"). Сформулированы правило приведения подобных членов и правило прибавления или вычитания к обеим частям уравнения одного и того же числа или выражения. В "Арифметике" Диофанта содержится много примеров действий над алгебраическими дробями. Преобразование выражений так же встречается в его трудах.

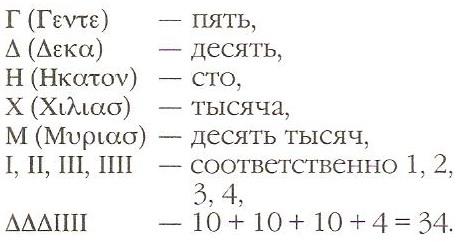
6. Самостоятельная работа. Сократите дробь:
Вариант I Вариант II
1)  1)
1) 
2)  2)
2) 
3)  3)
3) 
7. ФИЗКУЛЬТМИНУТКА
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
Налево, направо, вокруг посмотрели,
Открыли глаза, и снова за дело!
7. Объяснение новой темы.
Множители, на которые нужно умножить числитель и знаменатель каждой дроби, называются дополнительными множителями.
(Шпаргалка №2) Для того, чтобы привести несколько рациональных дробей к общему знаменателю, нужно:
разложить числитель и знаменатель каждой дроби на множители;
найти общий знаменатель всех этих дробей;
найти дополнительные множители для каждой дроби, они получаются путем деления общего знаменателя на знаменатель каждой из дробей;
умножить каждую из дробей на свой дополнительный множитель.
Пример 1. Приведите дробь  к знаменателю 35у3 .
к знаменателю 35у3 .
Решение. Так как 35у3 =7у · 5у2 , то, умножив числитель и знаменатель дроби на 5у2 , получим:
на 5у2 , получим: .
.
Первичное закрепление темы.
 1. Приведите дробь
1. Приведите дробь  к знаменателю х-2у.
к знаменателю х-2у.
2. Восстановите частично стертые записи:
8. Итоги урока. Рефлексия. Д/з.
- Какую цель мы поставили в начале урока?
-Мы достигли цели?
-Какие знания, полученные ранее, нам позволили «открыть» новое знание?
-Проанализируйте результат своей работы.
«Гора» Перед вами карточка с изображением горы. Если вы считаете, что хорошо усвоили на уроке, разобрались в изученной теме, то нарисуйте себя на вершине горы. Если осталось что-то неясно, нарисуйте себя ниже, а слева или справа решите сами.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Основное свойство дроби (258.79 KB)
Основное свойство дроби (258.79 KB)
 0
0 881
881 88
88 Нравится
0
Нравится
0









