| Предмет | Алгебра |
| Класс | 8 |
| Тема | Основное свойство дроби |
| Базовый учебник | Макарычев Ю.Н. и др. Алгебра. Учебник для 8 класса общеобразовательных учреждений. М.: Просвещение, 2013. 287 с. |
| Тип урока | Урок изучения нового материала |
| Оборудование | Классная доска, учебник, тетради, карточки с заданиями |
Цели урока:
Формирование знаний и умений по теме «Основное свойство дроби»:
а) объяснение и первичное закрепление материала;
б) отработка умений и навыков;
Повторение знания способов разложения на множители, формул сокращённого умножения;
Отработка навыков самоконтроля с целью освоения знаниями для выполнения различного вида заданий работы с выражениями;
Развитие вычислительных навыков;
Воспитание интереса к предмету, аккуратности и умения организовывать свое рабочее место.
Формы работы учащихся: фронтальная, индивидуальная, групповая
Технологическая карта урока:
| Этап урока | Деятельность учителя | Деятельность учеников | Время (мин.) |
| 1. Орг. момент
| Приветствует учащихся, проверяет готовность к уроку, включает в деловой ритм, зачитывает цитату | Приветствуют учителя, записывают тему урока, объясняют смысл цитаты | 2 |
| 2. Повторение учебного материала
| Проверяет готовность к восприятию новой темы | Записывают ответы в тетрадях, устно отвечают на вопросы учителя, работают с карточками, вспоминают способы разложения многочленов на множители | 8 |
| 3. Изучение нового материала
| Помогает сформулировать правило, исправляет ошибки и зачитывает притчу про «Забывчивого парикмахера» | Выполняют задания, с помощью учителя делают вывод, записывают правило, слушают доклад, работают с карточками | 10 |
| 4. Исследовательская работа
| Задает наводящие вопросы, объясняет полученные формулы | Отвечают на вопросы, записывают дополнительные формулы | 3 |
| 5. Работа у доски по заданиям учебника | Проверяет правильность выполнения заданий | Выполняют задания около доски и в тетрадях | 10 |
| 6. Самостоятельная работа (с самопроверкой) | Организует самостоятельное выполнение заданий и проверку | Самостоятельно выполняют задания в тетрадях. Проверяют свои работы и ставят оценки | 7 |
| 7. Подведение итогов урока | Организует деятельность учащихся по подведению итога урока, выставляет оценки | Отвечают на вопросы учителя | 2 |
| 8. Информация о домашнем задании | Информирует о домашнем задании, дает рекомендации по его выполнению | Записывают домашнее задание, выслушивают инструкции учителя по выполнению работы | 1 |
| 9. Рефлексия деятельности | Организует рефлексию | Осознают, что усвоено и выявляют возможные пробелы | 2 |
Итого: 45 мин.
Ход урока:
Организационный момент
«Знание только тогда знание, когда оно приобретено усилиями своей
мысли».
(Л. Н. Толстой)
– Как вы понимаете эти слова?
Повторение учебного материала:
а) – Среди данных дробей найдите рациональные. Запишите их в тетради.
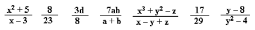
| – Какая дробь называется рациональной? |
|
| – Когда рациональная дробь равна нулю? | Разбор на примере последней дроби |
| – Когда рациональная дробь не имеет смысла? Почему? | |
| – Как найти допустимые значения дроби? |
Задания с кодовой записью ответов:
| Задания по вариантам | Ответы | Код | |
| Первый | Второй | ||
| № 1. Найдите значение переменной, при которой дробь равна нулю.
| № 1. Найдите значение переменной, при которой дробь равна нулю.
| 0 | 1 |
| 3 | 2 | ||
| –3 | 3 | ||
| вcе числа, кроме 0 | 4 | ||
| вcе числа, кроме –3 | 5 | ||
| вcе числа, кроме 3 | 6 | ||
| № 2. Найдите значение переменной, при которой дробь не имеет смысла.
| № 2. Найдите значение переменной, при которой дробь не имеет смысла.
| 0 | 7 |
| 3 | 8 | ||
| –3 | 9 | ||
| вcе числа, кроме 0 | 0 | ||
| вcе числа, кроме –3 | 1 | ||
| вcе числа, кроме 3 | 2 | ||
| № 3. Найдите допустимые значения переменной для дроби:
| № 3. Найдите допустимые значения переменной для дроби:
| 0 | 3 |
| 3 | 4 | ||
| –3 | 5 | ||
| вcе числа, кроме 0 | 6 | ||
| вcе числа, кроме –3 | 7 | ||
| вcе числа, кроме 3 | 8 | ||
Проверка правильности найденных ответов. (Самопроверка)
(1 вариант: 376; 2 вариант: 188)
б) – Сегодня на уроке нам потребуется умение раскладывать многочлены на множители. Как это можно сделать? (Применить способ вынесения общего множителя за скобки, способ группировки, знания формул сокращённого умножения.)
Вынесите за скобки общий множитель:
ab + ac = . . . 10xy2 – 6xy = . . .
Разложите на множители, используя способ группировки:
ax – bx + ay – by = . . .3a + 3b + ac + bc = . . .
Чтобы вспомнить способ разложения на множители с помощью формул сокращённого умножения, проверьте правильность формул, записанных на доске, и запишите в тетради код правильных ответов.
1) a2 + b2 – 2ab = (a – b)2
2) m2 + 2mn – n2 = (m – n)2
3) 2pt – p2 – t2 = (p – t)2
4) 2cd + c2 + d2 = (c + d)2
5) b2 + c2 = (b + c)(b – c)
6) x2 – y2 = (x – y)(x + y)
Изучение нового материала:
а) Подготовительная работа
Среди данных дробей есть равные. Конечно же, дроби не торопятся сообщить нам о своём “родстве”. Мы должны сами его обнаружить.
3/6, 1/2, 2/4, 1/3, 4/8, 2/5, 1/4, 3/9
– Как вы определили, что дроби равны? Каким правилом пользовались?
– Так в чём заключается основное свойство дроби?
б) Новая тема
А теперь попробуем применить это свойство для алгебраических дробей.
Запишите дроби, равные данной: 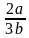 , со знаменателем 9b, с числителем 2а2.
, со знаменателем 9b, с числителем 2а2.
В тетрадях и на доске – запись:
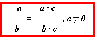
Дополните равенства:
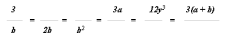
Проверка: 1-й числитель = 6, 2-й числитель = 3b, 1-й знаменатель = ab, 2-й знаменатель = 4by3, 3-й знаменатель = b(a + b) или ab + b2.
в) Сокращение дробей
– Проведём этот этап урока в игровой форме. Послушайте притчу про “Забывчивого парикмахера”.
Парикмахер по растерянности постриг волосы только с половины вашей головы. Если Вы, сокращая дроби, забудете разложить на множители её числитель и знаменатель, то Вы будете очень похожи на этого горе-мастера.
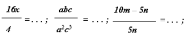
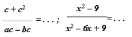
г) Задания с кодовой записью ответов
| Задания по вариантам. Сократите дроби: | Ответы | Код | |||
| Первый | Второй | ||||
| № 1.
a2 / (а2 – 3а) | № 1.
х2 / (х + ху) | 1 /(– 3а) | 0 | ||
| х2 /(х + у) | 1 | ||||
| х /(1 + ху) | 2 | ||||
| а /(а – 3) | 3 | ||||
| а /(а2 – 3) | 4 | ||||
| х /(1 + у) | 5 | ||||
| № 2.
(х2 – у2) / (х2 + ху) | № 2.
(2a – 2b) / (a2 – b2) | (– у2) / (ху) | 6 | ||
| 2 / (a – b) | 7 | ||||
| 2 / (– 1 ) | 8 | ||||
| (x – y ) /(x) | 9 | ||||
| (– y ) / x | 0 | ||||
| 2 / (a + b) | 1 | ||||
| № 3
39x7 / 13x3 | № 3.
17x5 / 34x6 | 2х | 2 | ||
| 3х | 3 | ||||
| 1 / 2х | 4 | ||||
| 1 / 17х | 5 | ||||
| 26 / х4 | 6 | ||||
| 3х4 | 7 | ||||
| 1 / 3х4 | 8 | ||||
| 26х4 | 9 | ||||
Проверка кодов:1 вариант: 397; 2 вариант: 514.
Исследовательская работа
– Как получена вторая дробь из первой?
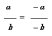
(Умножением и числителя, и знаменателя на –1.)
Последнюю дробь можно переписать, поставив один из минусов перед дробью:
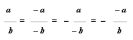
Работа у доски по заданиям учебника:
№ 27, № 29 (1-3), № 30 (1,2).
Самостоятельная работа (с самопроверкой)
№ 32 (1,2), 33(1). (Обсуждение ошибок, допущенных учащимися)
Подведение итогов урока, выставление оценок
Домашнее задание:
Учебник § 2, № 28 (1-2), 31 (1-5)
Рефлексия
«Микрофон»: Продолжите фразу: «Сегодня я узнал (а)». Поставьте себе оценку за урок.
9

 Получите свидетельство
Получите свидетельство Вход
Вход


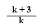
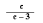









 Основное свойство дроби (42.87 KB)
Основное свойство дроби (42.87 KB)
 0
0 191
191 3
3 Нравится
0
Нравится
0


