Определители 2 порядка

• Определители

Определители широко применяются во многих разделах высшей математики, в теоретической механике, физике и т.д. для сокращения записей и удобства вычислений.

Определение.   Определитель матрицы   — это алгебраическая сумма  n!  слагаемых, составленных следующим образом. Каждое слагаемое — это произведение  элементов матрицы, взятых по одному из каждой строки и каждого столбца, со знаком плюс или минус, в зависимости от четности или нечетности перестановки

Правила вычисления определителей

Матрица первого порядка

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка

Равный самому элементу

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка =

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка =

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка =

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка =

Матрица первого порядка

Ей ставится в соответствие определитель первого порядка =

7

Определители 2 порядка

Определитель 2 - го порядка это число, равное произведению элементов главной диагонали минус произведение побочной диагонали

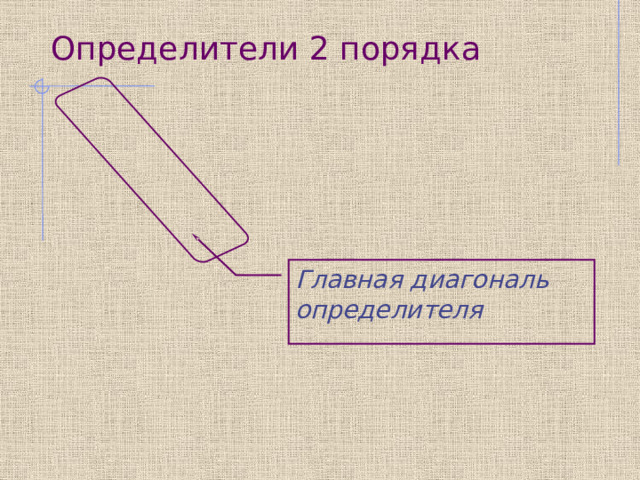
Определители 2 порядка

Главная диагональ определителя

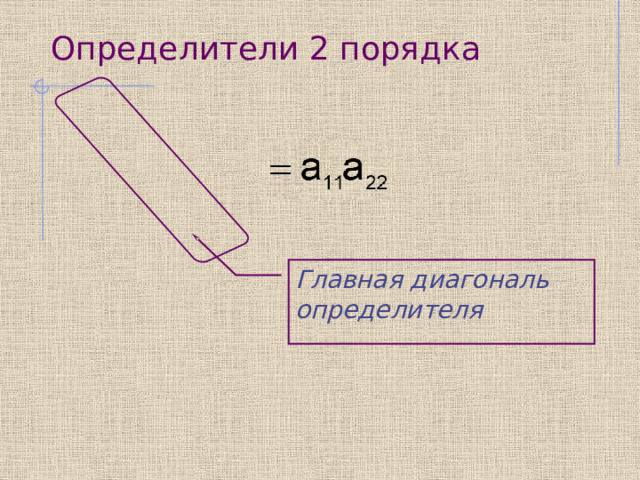
Определители 2 порядка

Главная диагональ определителя

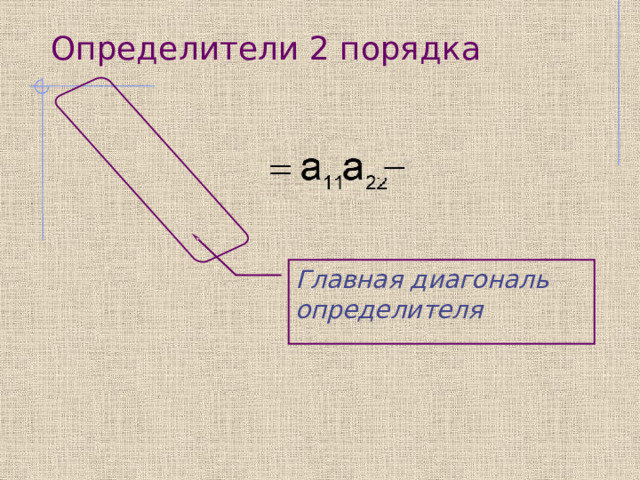
Определители 2 порядка

Главная диагональ определителя

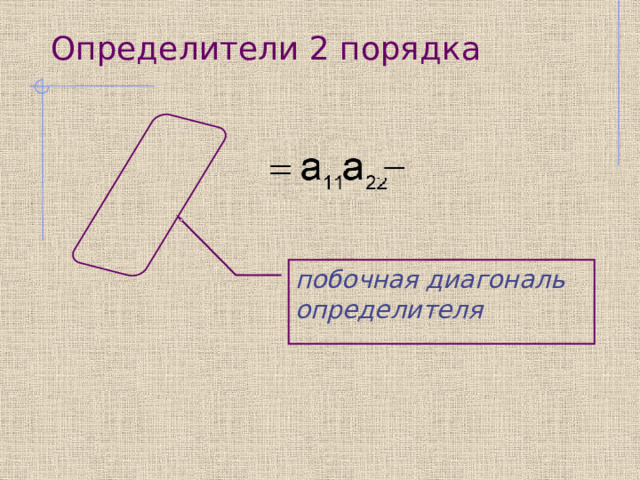
Определители 2 порядка

побочная диагональ определителя

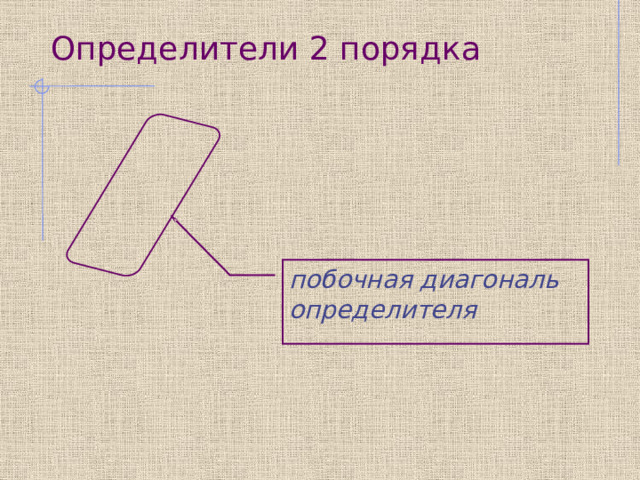
Определители 2 порядка

побочная диагональ определителя

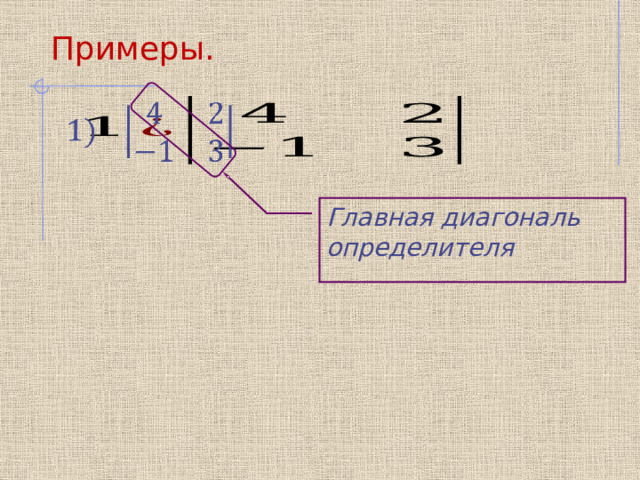
Примеры.

Главная диагональ определителя

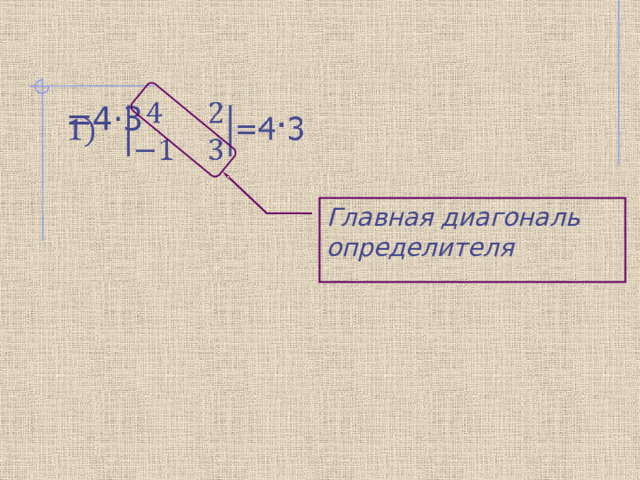
=4·3

Главная диагональ определителя

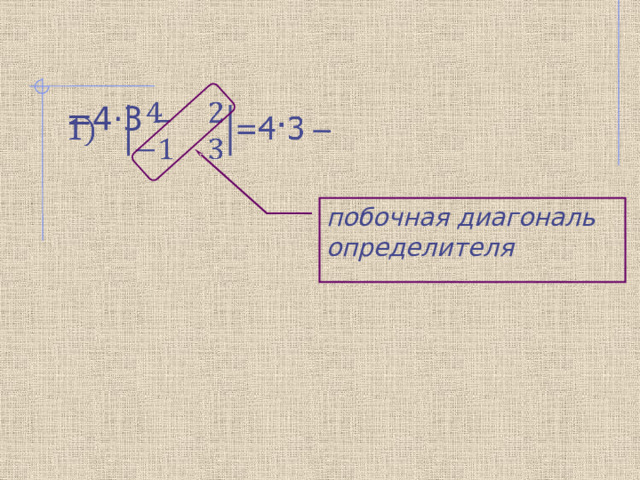
=4·3 –

побочная диагональ определителя

=4·3 – ( – 1)·2=14

Побочная диагональ определителя

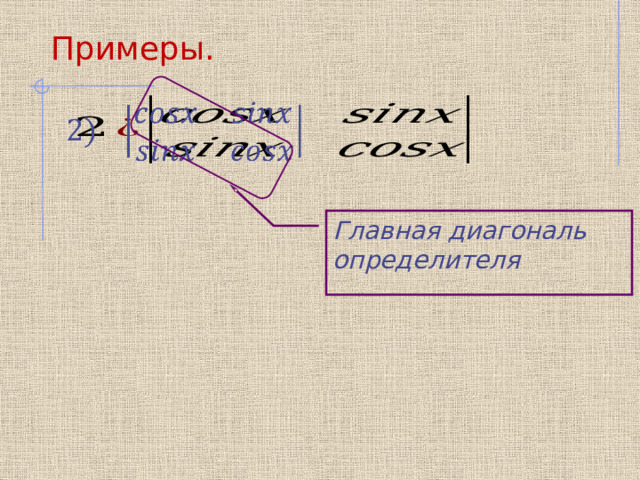
Примеры.

Главная диагональ определителя

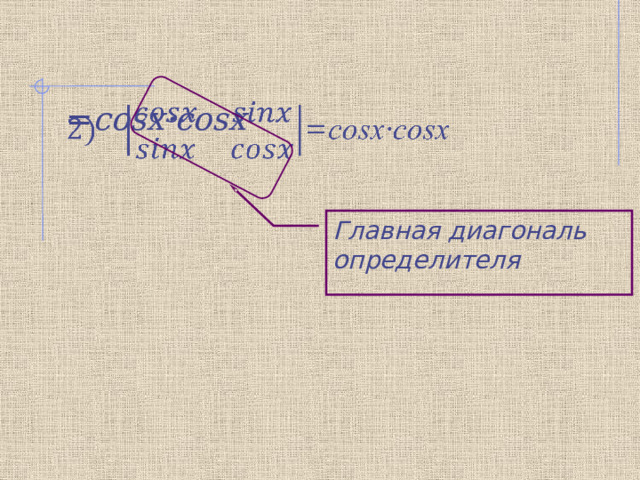
= cosx·cosx

Главная диагональ определителя

= cosx·cosx -

Побочная диагональ определителя

= cosx·cosx - sinx·sinx

Побочная диагональ определителя

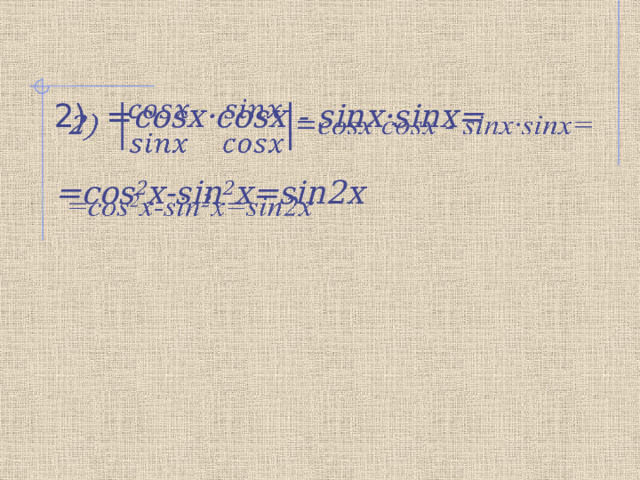
• = cosx·cosx - sinx·sinx=

=cos 2 x-sin 2 x=sin2x

Вычислить самостоятельно

1) 2) 3)

4) 5)