Олимпиадные задания по математике
(4 класс)
1. Сказала Баба-Яга Алёнушке: «Не сваришь к утру 100 кг каши – не видать тебе братца Иванушку». Заплакала Алёнушка: ведь она только 5 кг за час приготовить успевает. Но добрая мышка подарила девочке волшебный горшок, который варит каждый час 15 кг каши. За какое время справится Алёнушка с заданием, если и сама варить кашу будет, и горшок ей поможет?
2. Схватила лиса петушка и побежала в дремучий лес со скоростью 18 км/ч. Пришел кот домой через 2 часа, а петушка-то и нет. Бросился кот вдогонку со скоростью 24 км/ч. Через сколько времени спасет кот петушка?
3. Старик, имевший трех сыновей, распорядился, чтобы они после его смерти принадлежавшее ему стадо верблюдов так, чтобы старший взял половину всех верблюдов, средний – треть, а младший – девятую часть всех верблюдов. Старик умер и оставил 17 верблюдов. Сыновья начали дележ, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. Тогда братья обратились за советом к мудрецу. Тот приехал к ним на собственном верблюде и разделил по завещанию. Как он это сделал?
4. У тебя есть весы и две гири – на 2 г и на 5 г. Как с помощью этих гирь за три взвешивания разделить кусок масла весом 80 грамм на два куска весом 13 г и 67 г?
5. Борис, Андрей, Миша и Слава гуляли по парку с родителями и попросили их купить по стакану сока. Все ребята разного возраста (8Ю 9Ю 10 и 11 лет) и любят разные соки – грушевый, яблочный, вишневый и томатный. Определите их возраст и вкус, исходя из следующего:
1. Андрей старше Миши и мальчика, который любит яблочный сок, но младше того, кто любит томатный сок.
2. Мальчик, который любит яблочный сок – самый младший.
3. Борис и Андрей не любят грушевый сок.
4. Борис – не самый старший из мальчиков.
6. Найди неизвестное число.
| 13 | 11 | 15 |
| 7 | 1 | 13 |
| 15 | 10 | ? |
7. В зоопарке Толя видел двугорбых и одногорбых верблюдов, а также нерп. Он насчитал 16 животных, имеющих в общей сложности 44 ноги и 17 горбов. Скажите, сколько видел Толя одногорбых и двугорбых верблюдов и сколько нерп?
Ключи к ответам.
Если сразу будет варить в двух горшках, то за 1 час сварит:
5 + 15 = 20 (кг)
100 : 20 = 5 (ч)
Ответ: за 5 часов.
2.
1) 18 х 2 = 36 (км) – между ними, когда кот за лисой бросился вдогонку
2) 24 – 18 = 6 (км/ч) – за 1 час кот приближается (разность скоростей)
3) за 1 час кот приближается на 6 км
за 2 ч – на 12 км
за 3 ч – на 18 км
36 : 6 = 6 (ч) – за это время кот догонит лису.
Ответ: через 6 часов.
3.
1) 17 + 1 = 18 (в.)
2) 18 : 2 = 9 (в.) – часть старшего брата
3) 18 : 3 = 6 (в.) – часть среднего брата
4) 18 : 9 = 2 (в.) – часть младшего брата.
Своего верблюда мудрец забрал обратно.
4.
Разделим кусок мыла на два одинаковых куска по 40 г (первое взвешивание). Разделим один из кусков еще раз пополам на куски по 20 г (второе взвешивание). Теперь положим на одну чашу весов кусок по 20 г, на другую - обе гири (2 г + 5 г = 7 г). Чтобы уравновесить весы надо убрать 13 г. Осталось соединить куски: 40 г + 20 г + 7 г = 67 г.
5.
|
| 8 | 9 | 10 | 11 | груша | вишня | яблоко | томат |
| Борис | + |
|
|
|
|
| + |
|
| Андрей |
|
| + |
|
| + |
|
|
| Миша |
| + |
|
| + |
|
|
|
| Слава |
|
|
| + |
|
|
| + |
6.
(13 – 11) + 13 = 15
(7 – 1) + 7 = 13
(15 – 10) + 15 = 20
7. У нерп ног нет, значит44 ноги принадлежат 11 верблюдам. Их было 6 двугорбых и 5 одногорбых. Нерп было 5.
1. Марина и Наташа купили фрукты.
Марина купила 3 яблока и 4 груши и уплатила 18 рублей. Наташа купила 6 яблок и 12 груш и уплатила 48 рублей. Сколько стоит 1 яблоко? Сколько стоит 1 груша?
(5 баллов)
2. На трех деревьях 36 галок. Когда с первого дерева перелетели на второе 6 галок, а со второго перелетели на третье 4 галки, то на всех деревьях галок оказалось поровну. Сколько галок первоначально сидело на каждом дереве?
(5 баллов)
3. В оранжерее были срезаны гвоздики: белых и розовых – 400 штук, розовых и красных - 300 штук, белых и красных – 440 штук. Сколько гвоздик каждого цвета срезали в оранжерее?
(5 баллов)
4. В саду росли яблони и вишни. Если взять ½ всех вишен и ¼ всех яблонь, то тех и других деревьев будет поровну, а всего деревьев в саду 360. Сколько яблонь и вишен было в саду?
(5 баллов)
5. Периметр нижнего квадрата 24 см. Периметр верхнего – на 8 см меньше. Найдите площадь наименьшего квадрата, если известно, что сторона нижнего квадрата при пересечении со стороной верхнего квадрата делит его сторону пополам.
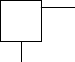
6. Расставь скобки.
7 х 9 + 12 : 3 – 2 = 23
7 х 9 + 12 : 3 – 2 = 75
7 х 9 + 12 : 3 – 2 = 47
(по 1 баллу за каждое равенство)
Ключи к ответам.
1. Рысь съедает 600 кг мяса за 6 часов, а тигр – в 2 раза быстрее. За какое время они съедят это мясо вместе?
2.Как разделить пирог четырехугольной формы двумя разрезами на 4 части так, чтобы две части были четырехугольные, а две – треугольные? А три арбуза на четверых? Нарисуй.
3. Пять учеников купили 100 тетрадей. Коля и Вася купили 52 тетради. Вася и Юра – 43 тетради. Юра и Саша – 34 тетради, Саша и Сережа – 30. Сколько тетрадей купил каждый из них?
4. Сколько ведер воды находится в 9 одинаковых бочках, если в 21 такую же бочку налито 98 ведер воды?
5. В соревнованиях по лыжам участвовали Юра, Миша, Володя, Саша и Олег. Юра пришел к финишу раньше Миши, но позже Олега. Володя и Олег не пришли друг за другом, а Саша не пришел друг за другом ни с Олегом, ни с Володей. В каком порядке пришли к финишу мальчики?
6. Восстанови запись. Одинаковые буквы обозначают одинаковые цифры.
| А + | Б | В | Г | Б | 9 |
|
| А | Б | В | Г | Б |
| 3 | 0 | 6 | 2 | 1 | 6 |
Ключи к ответам
1) 600 : 6 = 100 (кг) – за час съедает рысь.
6 : 2 = 3 (ч) – ел тигр.
100 + 200 = 300 ( кг) – за час съедают тигр и рысь вместе.
600 : 300 = 2 (ч)
Ответ: 2 ч.
2.
3. 1) 52 + 34 = 86 (т.) – купили Коля, Вася, Юра и Саша.
2) 100 – 86 = 14 (т.) – купил Сережа.
3) 30 – 14 = 16 (т.) – купил Саша.
4) 34 – 16 = 18 (т.) – купил Юра.
5) 43 – 18 = 25 (т.) – купил Вася.
6) 52 – 25 = 27 (т.) – купил Коля.
Ответ: Юра – 18 т., Вася – 25 т., Коля – 27 т., Саша – 16 т., Сережа – 14 т.
4. Если в 21 бочке находится 98 ведер воды, то в 3-х бочках их в 7 раз меньше, то есть 98 : 7 = 14 ведер. Поэтому в 9 бочках воды в три раза больше, то есть 13 х 3 = 42 ведра.
Ответ: 42 ведра.
5. Первым к финишу пришел Олег, за ним Юра, за Юрой – Володя, заием – Миша. Последним пришел Саша.
6.
| 2 | 7 | 8 | 3 | 7 | 9 |
|
| 2 | 3 | 8 | 7 | 7 |
| 3 | 0 | 6 | 2 | 1 | 6 |
Способы оценивания.
Представлено верное решение и дан ответ – 4 балла. Верное решение, но нет пояснений и (или) ответа – 3 балла. За ошибки вычислительного характера снимается 1 балл. Ход решения верный, но решение не доведено до конца – 1 балл.
Правильно разделен прямоугольник и арбузы – 3 балла. Правильно разделены арбузы – 2 балла.
Представлено верное решение и дан ответ – 3 балла. Представлен верный ход решения, но нет пояснения или ответа – 3 бала. За ошибки вычислительного характера снимается 1 балл. Ход решения верный, но решение не доведено до конца – 1 балл.
Представлено верное решение и дан ответ – 6 балла. Верное решение, но нет пояснений и (или) ответа – 5 балла. Дан только ответ- 3 балла. Ход решения верный, но решение не доведено до конца – 1 балл.
Представлено верное решение с пояснением. – 5 баллов. Дан ответ без пояснений схем и рисунков – 3 балла. За каждую ошибку снимается 1 балл.
По одному баллу за расшифровку каждой из букв (А, Б, В, Г) – 4 балла.
1. Савва, Руслан, Митя и Игорь шили шапки: двое - из лисы, двое – из кролика. Руслан и Савва, Савва и Игорь шили из разного меха. Митя – из лисы. Из чего шил Игорь?
(2 балла)
2. Таня и Зоя засушили васильки и ромашки. Таня засушила ромашек на две меньше, чем васильков, которых у неё было на один больше, чем у Зои. У Зои васильков было на 2 больше, чем ромашек. У кого цветов было засушено больше?
(3 балла)
3. Если год возникновения Москвы увеличить на две единицы и полученное число уменьшить в три раза, то в частном получим число, которое меньше 400 на 17. В каком году возникла Москва?
(4 балла)
4. Каменщик укладывает 4000 кирпичей за 8 ч, а монтажник краном укладывает один блок, заменяющий 800 кирпичей, за 16 минут. Во сколько раз меньше времени требуется монтажнику, чтобы уложить блоки, заменяющие 4000 кирпичей?
(4 балла)
5. В пакете имеются конфеты двух сортов: ириски и карамели. Карамелька тяжелее ириски в 2 раза, но зато ирисок в пакете в 6 раз больше. Сколько весят конфеты, если общий вес карамели равен 500граммам?
(5 баллов)
6. Отцу 45 лет, сыну 18 лет. Через сколько лет отец будет вдвое старше сына?
(5 баллов)
7. На скотном дворе гуляли гуси и поросята. Сын спросил у отца: «Папа, сколько у нас гусей и сколько поросят?»
Папа ответил: «А вот угадай-ка сам: число всех голов - 30, число всех ног – 84». Сын подумал и решил задачу. Как он решал её?
(5 баллов)
Ключи к ответам.
Игорь шил из кролика.
У Тани цветов больше.
1147 г. Решение: 1) 400 – 17 = 383; 2) 383 х 3 = 1149; 3) 1149 – 2 = 1147
В 6 раз.
2000 г.
Через 9 лет.
1) 2 ноги х 30 = 60 ног; 2) 84 ноги – 60 ноги = 24 ноги; 3)4 ноги – 2 ноги = 2 ноги; 4) 24 : 2 ноги = 12 поросят; 5) 30 голов – 12 голов = 18 голов (гусей)
1. В кошельке у Миши три монеты: 5 рублей, 2 рубля, 1 рубль. Какую сумму он не сможет заплатить без сдачи?
А – 3 рубля В – 4 рубля С – 7 рублей Д – 8 рублей
Выбери правильный ответ
(2 балла)
2. На заседании присутствуют 29 академиков, 12 из них имеют бороды, а 18 усы. У трёх академиков нет ни бороды, ни усов. Сколько академиков имеют и бороды и усы?
(5 баллов)
3. Цифрами 0 1 2 3 запиши наибольшее и наименьшее шестизначное число так, чтобы в записи числа участвовала каждая из заданных цифр не менее одного раза
(2 балла)
4. Пирог прямоугольной формы двумя разрезами разделите на 4 части так, чтобы две из них были четырёхугольной формы, а две – треугольной формы.
(4 балла)
5. Три черепахи – Анди, Банди, Канди – соревнуются в беге на дистанцию 300 м. Они стартовали одновременно. Когда Анди финишировала, Банди оставалось до финиша 10 м, а Канди была на 4 м впереди Банди. На каком расстоянии до финиша будет Банди, когда Канди закончит дистанцию, если каждая черепаха движется с постоянной скоростью?
(6 баллов)
6. В цветочный магазин привезли розы: белых и розовых – 400 штук, розовых и красных – 300 штук, белых и красных – 440 штук. Сколько роз каждого цвета завезли в магазин?
(5 баллов)
Ключи к ответам.
1. 4 рубля.
2.
29 – 3 = 26(ак.)
26 – 18 = 8 (ак.)
12 – 8 = 4 (ак.)
29 – 3 = 26 (ак.)
12 + 18 = 30 (ак.)
30 – 26 = 4 (ак.)
3. 333210, 100023
4.
5. 5 метров.
1) 400 + 440 = 840 (р.) – двойное количество белых роз, розовых и красных..
2) 840 – 300 = 540 (р.) – двойное количество белых.
3) 540 : 2 = 270 (р.) – белых.
4) 400 – 270 = 130 (р.) – розовых.
5) 300 – 130 = 170 (р.) – красных.
1. В столовую привезли карпов, сазанов, судаков и лещей. Карпов было 46 кг, сазанов – 30 кг, а судаков в 3 раза больше, чем лещей. Когда половину всей рыбы израсходовали, то осталось ещё 90 кг. Сколько килограммов судака привезли в столовую?
(5 баллов)
2. Восстанови запись. Одинаковые буквы обозначают одинаковые цифры.
(2 балла)

3. Расшифруй запись: ☻ ☻ + ☻ ☻ ☻ = ☻ ☻ ☻ ☻, если известно, что оба слагаемые не изменятся, если прочитать их справа налево.
(1 балл)
4. Мать для трёх сыновей оставила тарелку слив. Первым проснулся старший сын. Он съел 1/3 часть и ушёл. Второй, думая, что его братья ещё не ели слив, съел 1/3 часть и ушёл. Трети сын съел 1/3 часть оставшихся слив. Когда пришла мама, то насчитала 8 слив. Сколько слив было сначала?
(3 балла)
На столе лежат 4 фигуры.
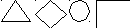
5. Цвета этих фигур: жёлтый, синий, красный. Фигура красного цвета лежит между зелёной и синей. Справа от жёлтой фигуры лежит ромб. Круг лежит правее треугольника и ромба, причём треугольник лежит не с кругом. Фигура синего цвета не лежит рядом с фигурой жёлтого цвета. В каком порядке лежат фигуры, какого цвета каждая из них?
(4 балла)
6. квадратный участок земли (длина стороны – 40 м) состоит из 16 квадратных грядок. Для орошения участка надо проложить трубу между грядками от т. А. Эта труба длиной 100 м должна разделить на 2 равные части участок. Как её проложить?
(4 балла)

 Получите свидетельство
Получите свидетельство Вход
Вход











 Олимпиада по математике (87.5 KB)
Олимпиада по математике (87.5 KB)
 0
0 474
474 1
1 Нравится
0
Нравится
0




