Октаэдр представляетс собой пересечение двух тетраэдров.
Внутренняя (общая) часть конфигурации из двух двойственных тетраэдров является октаэдром, а сама эта конфигурация называется звёздчатым октаэдром (лат.: stella octangula).
Конфигурация является единственнойзвёздчатой формой октаэдра. Соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырёх правильных тетраэдров с половиной длины ребра (то есть полного усечения[en] тетраэдра).
Вершины октаэдра лежат на серединах рёбер тетраэдра и октаэдр связан с тетраэдром тем же образом, каккубооктаэдр и икосододекаэдр связаны с остальными платоновыми телами.
Можно разделить рёбра октаэдра в отношении золотого сечения для определения вершин икосаэдра. Для этого следует расположить вектора на рёбрах, так, чтобы все грани были окружены циклами.
Затем делим каждое ребро в золотом отношении вдоль векторов. Полученные точки являются вершинами икосаэдра.
Октаэдры и тетраэдры[en] можно чередовать, чтобы построить однородные относительно вершин, рёбер и гранейсоты, которые Фуллер назвал октетной связкой[en].
Это единственные соты, позволяющие регулярную укладку в кубе, и они являются одним из 28 видов выпуклых однородных сот[en].
Октаэдр уникален среди платоновых тел в том, что только он имеет чётное число граней при каждой вершине.
Кроме того, это единственный член этой группы, который имеет плоскости симметрии, не пересекающие ни одну грань.
Если использовать стандартную терминологию многогранников Джонсона, октаэдр можно назвать квадратной бипирамидой. Усечение двух противоположных вершин приводит к усечённой бипирамиде[en].

Октаэдр является 4-связным. Это значит, что нужно удалить четыре вершины, чтобы разъединить оставшиеся.
Это один из всего лишь четырёх 4-связныхсимплициальных[en] хорошо покрытых многогранников, что означает, что все наибольшие независимые множества вершин имеют один и тот же размер.
Другие три многогранника с этим свойством — пятиугольная бипирамида[en], плосконосый равногранный тетраэдр[en] и нерегулярный многогранник с 12 вершинами и 20 треугольными гранями [2].
Октаэдр можно вписать в тетраэдр, притом четыре из восьми граней октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести ребер тетраэдра.
Октаэдр можно вписать в куб, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
В октаэдр можно вписать куб, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
Однородное раскрашивание и симметрия [править | править вики-текст]
Имеется 3 однородных раскрашивания[en] октаэдра, названных по их цветам граней: 1212, 1112, 1111.
Группой симметрии октаэдра является Oh с порядком 48, трёхмерная гипероктаэдральная группа[en].
В подгруппы этой группы входят D3d (порядка 12), группа симметрии треугольной антипризмы, D4h (порядка 16), группа симметрии квадратной бипирамиды, и Td (порядка 24), группа симметрииполностью усечённого тетраэдра.
Эти симметрии можно подчеркнуть путём различного раскрашивания граней.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход






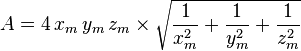
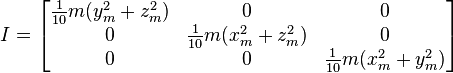









 Октаэдр - правильные многогранники (методическая разработка) (0.12 MB)
Октаэдр - правильные многогранники (методическая разработка) (0.12 MB)
 0
0 1809
1809 91
91 Нравится
0
Нравится
0



