Обратные функции

Обратная функция

Задачи урока:

Сформировать умения оперировать понятиями обратимой функции, взаимно обратных функций; применять свойства взаимно обратных функций; находить функцию, обратную данной.

Актуализация знаний:

Выполнить №№ 2.13; 2.14.

Практическая работа

Постройте в одной системе координат графики функций:

Выразите переменную x из второго и третьего равенств

Что заметили?

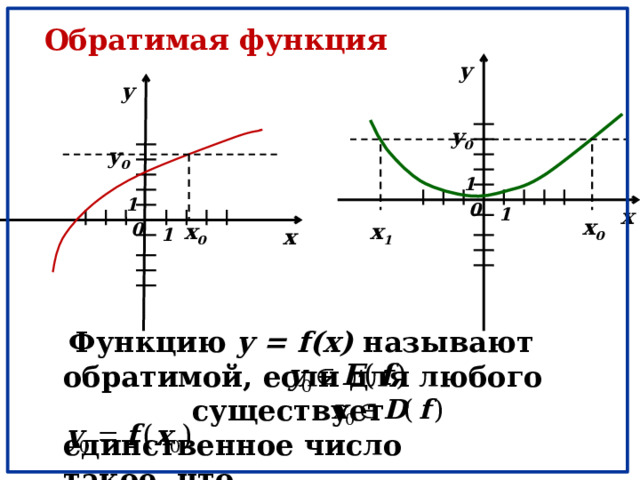
Обратимая функция

y

y

y 0

y 0

1

1

0

x

1

x 0

x 1

0

x 0

1

x

Функцию y = f(x) называют обратимой, если для любого существует единственное число такое, что

Обратимая функция

Если функция является возрастающей (убывающей) на всей области определения, то она является обратимой.

Примеры обратимых функций:

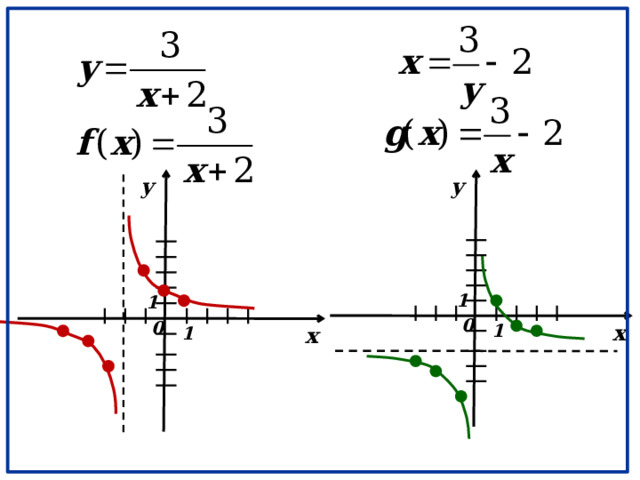
y

y

1

1

0

0

1

x

x

1

Свойства функций:

1

2

Взаимно обратные функции

Функции f и g называются взаимно обратными, если:

1.

2. Для любого из равенства

следует, что , то есть .

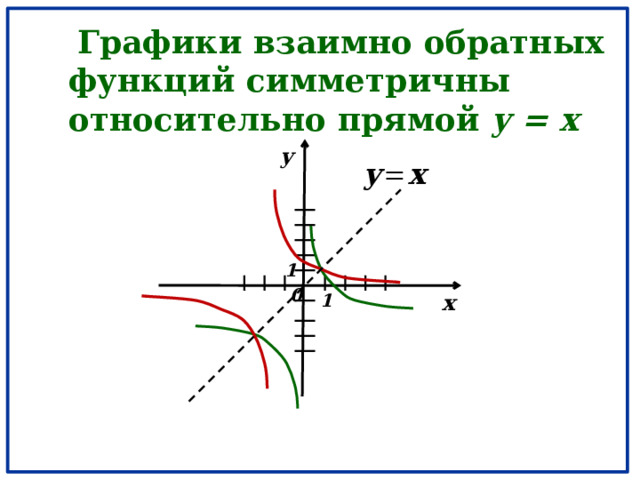
Графики взаимно обратных функций симметричны относительно прямой y = x

y

1

0

1

x

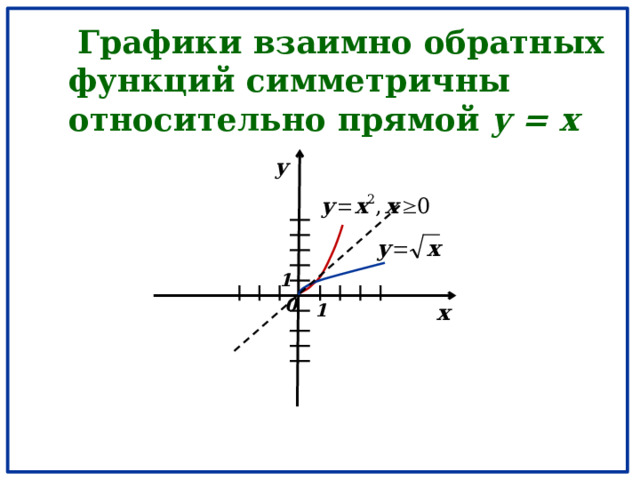
Графики взаимно обратных функций симметричны относительно прямой y = x

y

1

0

x

1

Если функция f является возрастающей (убывающей), то обратная к ней функция g является тоже возрастающей (убывающей).

Решение задач:

№№ 3.1; 3.3; 3.4; 3.6; 3.8; 3.10;

3.12; 3.13.

Дома:

№№ 3.2; 3.5; 3.7; 3.9; 3.11; 3.18.