Обобщающий урок математики по теме Производная функции

Обобщающий урок математики по теме "Производная функции".

• Девиз урока:
• Скажи мне, и я забуду покажи мне, и я запомню Дай действовать самому И я научусь.
• Конфуций

Цели урока:

• Обобщить теоретические знания по теме: «Производная. Геометрический и физический смысл производной. Уравнение касательной»;

• Рассмотреть решение задач, связанных с этой темой, базового и повышенного уровней сложности;

• Организовать работу учащихся по указанной теме на уровне соответствующем уровню уже сформированных у них знаний.

Задачи:

• Повторить алгоритм нахождения производной.

• Используя правила нахождения производной, применить их для решения конкретных задач.

• Сформировать глубину и оперативность мышления.

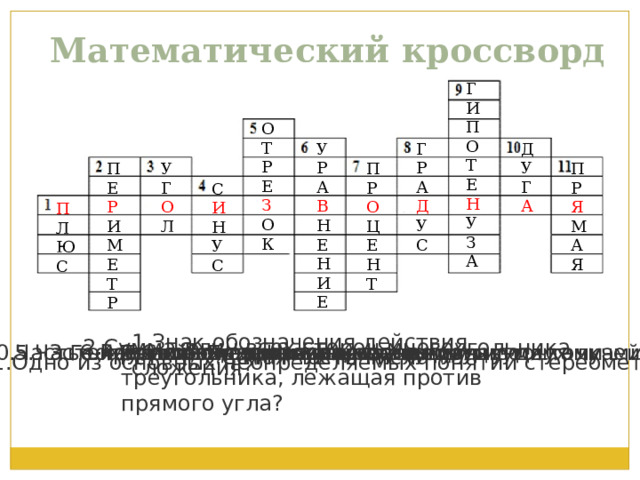
Математический кроссворд

Г

И

П

О

Т

Е

Н

У

З

А

О

Т

Р

Е

З

О

К

Д

Г

У

Р

У

Р

А

А

Г

В

Д

А

У

Н

Е

С

Н

И

Е

П

П

П

У

Г

Е

Р

Р

Р

Я

О

О

И

М

Л

Ц

А

Е

М

Н

Е

Я

Т

Т

Р

С

И

Н

У

С

П

Л

Ю

С

1.Знак обозначения действия сложения?

2.Сумма длин всех сторон многоугольника

8.Единица измерения угла

9.Сторона прямоугольного треугольника, лежащая против прямого угла?

3.Геометрическая фигура, состоящая из двух лучей

5.Часть прямой,заключенная между двумя точками

6.Равенство, содержащее переменную

10.Часть окружности, заключенная между двумя точками?

4.Тригонометрическая функция

7.Сотая часть числа

11.Одно из основных неопределяемых понятий стереометрии?

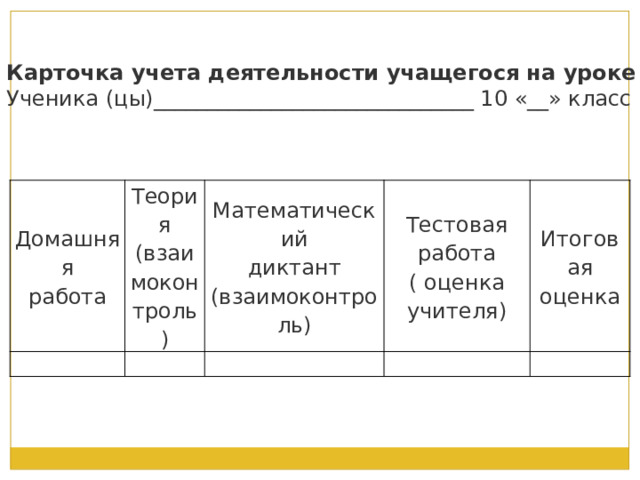
Карточка учета деятельности учащегося на уроке

Ученика (цы)______________________________ 10 «__» класс

Домашняя

работа

Теория

(взаимоконтроль)

Математический

диктант

Тестовая работа

( оценка учителя)

(взаимоконтроль)

Итоговая оценка

Вопросы к зачету по теме «Производная»

• 1. Что такое дифференцирование.

• 2. Правила дифференцирования.

• 3. Таблица дифференцирования

• 4.  В чем состоит механический смысл производной функции.

• 5.  В чем состоит геометрический смысл производной функции.

• 6.  Уравнение касательной к графику функции.

Математический диктант

1) f ( x ) = 2 x – 3 2) f ( x ) = 3 x 4 – 7 x 3 + 2 x 2 +9 3) f ( x ) = x 3 +2 4) f ( x ) = (3 – 4 x ) 2 5) f ( x ) = ( х 3 –2 x ) 2 6) f ( x ) = (1 + 2 х )(1 – 2 х ) 7) f ( x ) = 2 sin x 8) f ( x ) = –1/3 cos (3 x + π/4) 9) f ( x ) = ctg (2 – 5 x ) 10) f ( x ) = 2 x 3  – 3sin3 x

1) f '( x ) = 12 x 3 – 21 x 2 + 4 x 2) f ( x ) = – 8(3 – 4 x ) 3)  f '( x ) = – 8 x 4)  f '( x ) = 2 5)  f '( x ) = 2(3 x 2 – 2) ( x 3 – 2 x ) 6)  f '( x ) = sin (3x + π/4) 7)  f '( x ) = 5/ sin 2 (2 – 5 x ) 8)  f '( x ) = 6 x 2 – 9cos 3 x 9) f ( x ) = 2 cos x 10) f '( x ) = 3 x 2

Проверь себя

номер функции

номер составляющей производной

1

2

4

3

1

4

10

2

5

5

6

3

7

8

9

9

6

7

10

8

10 – «5» 8 – 9 – «4» 6 – 7 – «3» 5 – 0 – «2»

Физкультминутка

Однажды великого греческого философа Сократа спросили о том, что, по его мнению, легче всего в жизни. Он ответил, что легче всего поучать других, а труднее – познать самого себя. Мы познаем окружающий нас мир. Но сегодня давайте заглянем в себя. Как мы воспринимаем окружающий мир? Как художники или как мыслители?

Психологический тест

Подведем итоги, учитывая, что результат «ЛЛЛ» соответствует художественному типу личности, а «ППП» – типу мыслителя. (Эти различия связаны с функциональной асимметрией мозга человека: у «художников» более развитое правое полушарие и преобладает образное мышление, у «мыслителей» – соответственно – левое полушарие и логическое мышление). Какой же тип мышления преобладает у Вас? Несколько «мыслителей», несколько «художников», большинство – личности, которым свойственно и логическое и образное мышление.

1) Переплетите пальцы рук. Большой палец правой или левой руки оказался у Вас сверху? Запишите результат буквами «Л» или «П».

2) Скрестите руки на груди (поза «Наполеона»). Кисть, какой руки оказалась сверху? Запишите результат.

3) Изобразите «бурные аплодисменты». Ладонь, какой руки у Вас сверху? Запишите.

Дополнительные задачи

• Решите неравенство   f'(x) + g'(x)  0, если  f(x) =2х 3 + 12x 2 , g(x) =9х 2 + 72x

• Решите уравнение f'(x) = 0,  если f(x) = 3sinx – 4cosx – 2x

Ответы:

• Ответ:[– 4; – 3]

• Ответ:

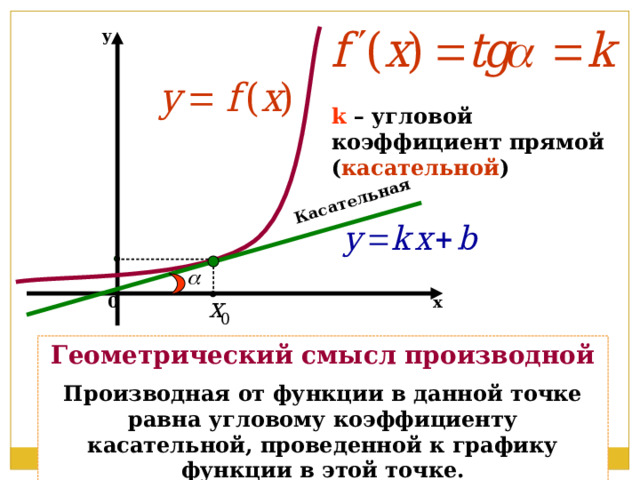
Касательная

y

k – угловой коэффициент прямой ( касательной )

0

х

Геометрический смысл производной

Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

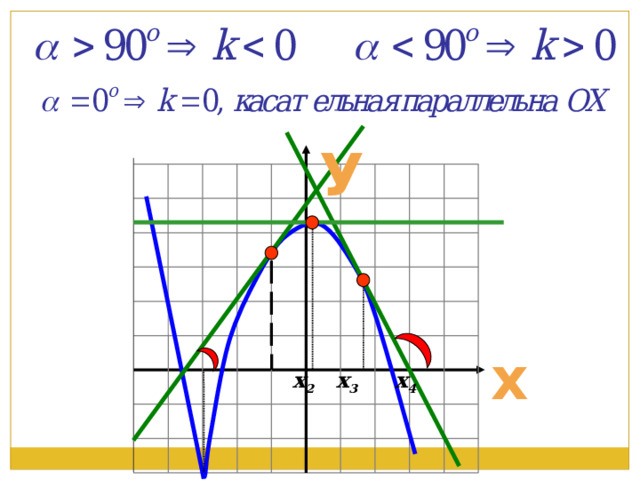
У

х

х 2 х 3 х 4

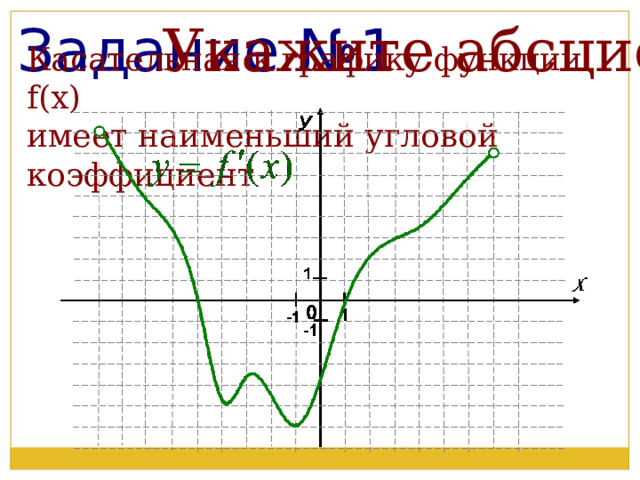
Задание №1

Укажите абсциссу точки, в которой

Касательная к графику функции f(x)

имеет наименьший угловой коэффициент

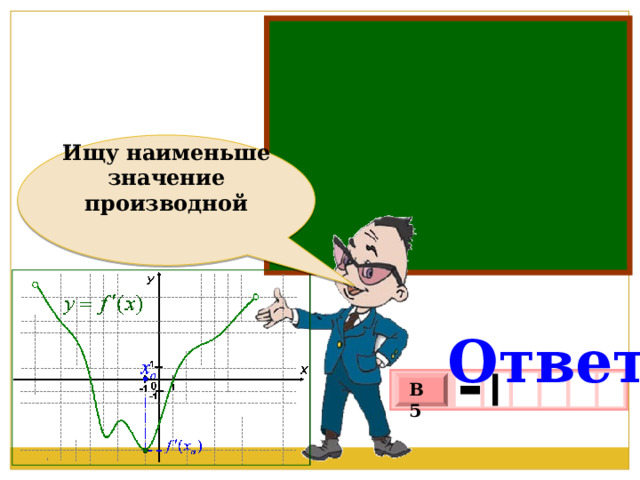
Ищу наименьше значение производной

Ответ:

-

В 5

х

3

х

1

0

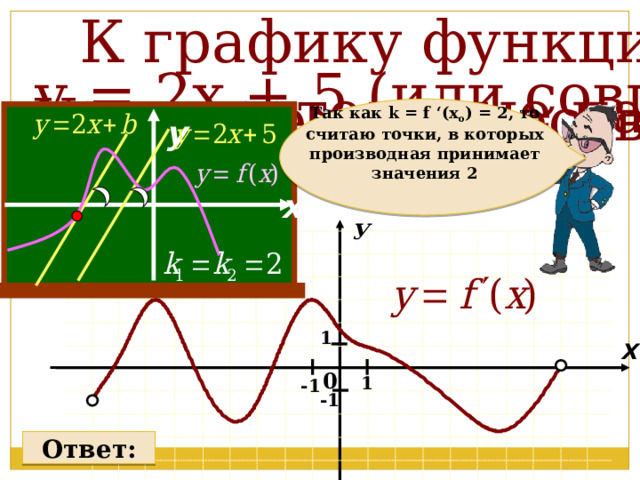
К графику функции у = f(x) провели

все касательные параллельные прямой

у = 2х + 5 (или совпадающие с ней).

Укажите количество точек касания.

Так как k = f ‘(x o ) = 2, то считаю точки, в которых производная принимает значения 2

у

х

У

1

Х

0

1

-1

-1

Ответ:

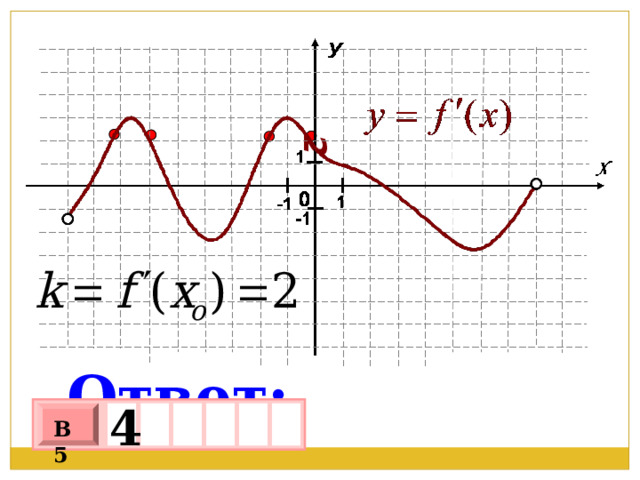
2

Ответ:

-

4

х

3

В 5

х

1

0

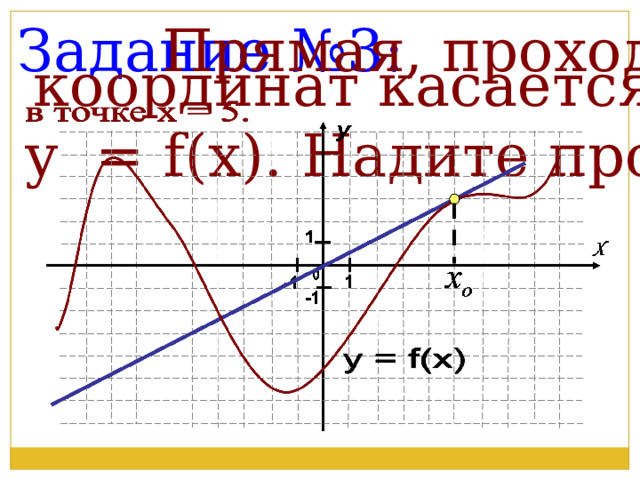
Задание №3:

Прямая, проходящая через начало

координат касается графика функции

у = f(x). Надите производную функции

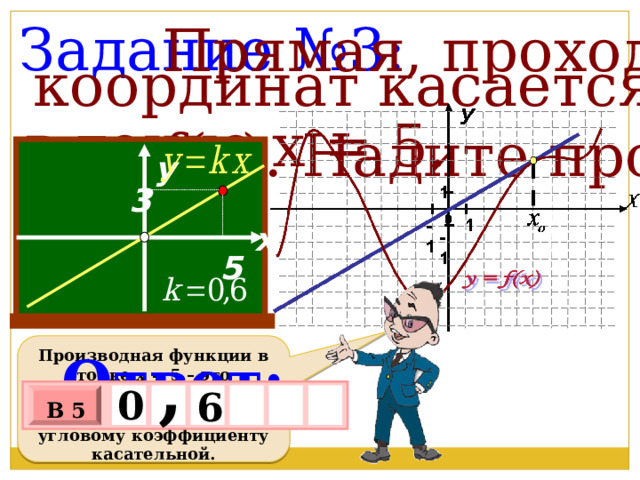
Задание №3:

Прямая, проходящая через начало

координат касается графика функции

у = f(x). Надите производную функции

в точке х = 5.

у

3

х

5

Производная функции в точке х = 5 – это производная в точке касания х о , а она равна угловому коэффициенту касательной.

Ответ:

,

-

0

6

х

3

В 5

х

1

0

• Тестовые задания в формате ЕГЭ в 5-ти вариантах.

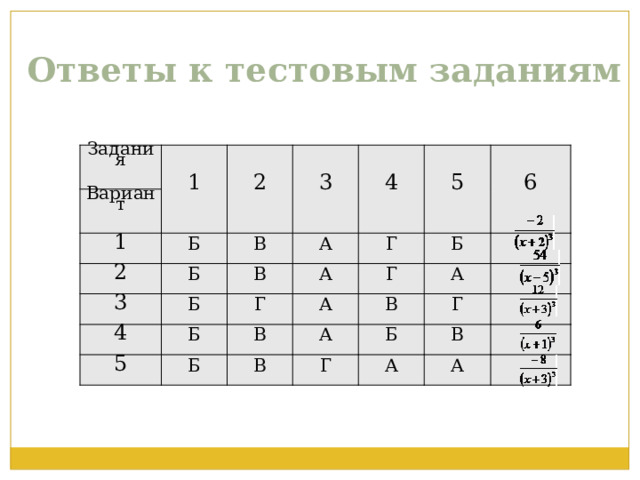
Ответы к тестовым заданиям

Задания

1

Вариант

2

1

Б

3

2

Б

3

В

4

5

А

Б

4

В

А

6

Г

5

Г

Б

Б

А

Б

Г

В

В

А

В

А

Г

Г

Б

В

А

А

Домашнее задание.

• № 28.40 (а,б)
• № 28.41 (б)
• № 28.45 (а,б)

Ну кто придумал эту математику !

У меня всё получилось!!!

Надо решить ещё пару примеров.

Спасибо за работу!