Тема: «Производная функции»
Цели урока:
образовательная: обобщение, повторение и систематизация знаний по теме «Производная функции», вырабатывать навыки нахождения производной, применять их при решении конкретных задач;
развивающая: развивать логическое мышление, внимание, интерес к предмету, стремление глубже усвоить предмет;
воспитательная: воспитывать интерес к математике и физике, воспитывать чувство ответственности, организованности, настойчивости и упорства в достижении цели.
Тип урока: урок закрепления и обобщения знаний.
Оборудование: интерактивная доска, тесты.
Межпредметная связь: геометрия, физика,литература.
План урока:
Организационный момент.
Устная работа.
Решение примеров.
Физический и геометрический смысл производной.
Тестовая работа.
Ромашка Блума.
Домашнее задание.
Итог урока.
Ход урока.
1.Организационный момент.
Сегодня у нас обобщающий урок по теме «Производная». Наша задача – повторить теоретический материал и закрепить умения и навыки в процессе выполнения различных задач.
2. Устная работа.
В каждой функции от х, нареченной игреком,
Вы фиксируете х, отмечая индексом.
Придаете вы ему тотчас приращение,
Тем у функции самой вызвав изменение.
Приращений тех теперь, взявши отношение,
Побуждаете к нулю у ΔХ стремление
Предел такого отношения вычисляется,
Он производной в науке называется.
А теперь на математическом языке дадим определение производной. Что такое производная? Если разностное отношение  =
= 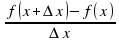 имеет предел при
имеет предел при  то этот предел называют производной функции у = f(х) в точке х.
то этот предел называют производной функции у = f(х) в точке х.
Вспомним все формулы и напишем на доске.
С '= 0 ( sin x)' = cos x
(Сх) '= С ( cos x)' = - sin x
( хn) '= nxn-1 ( tg x)' = 
( uv) '= u'v + uv' ( ctg x)'= - 
( 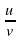 )
)
3. Решение примеров.
Используя данные формулы, решить примеры.
Найти производные функций:
у = 2х5+6х3-4х+1;
у = (3х-1)9;
у = ( х2+3)(х-2);
у = 
у = sin x+8x;
y = ctgx-4x3.
4. Физический и геометрический смысл производной.
Что объединяет этих ученых?




Евклид Архимед Декарт Ферма
- Евклид дал способ построения касательной к окружности.
- Архимед построил касательную к спирали.
- Декарт нашел первый общий способ построения касательной
к алгебраической кривой.
- Ферма дал метод построения касательных.
Этих ученых объединяет то, что все они занимались вопросами построения касательных к произвольной плоской кривой.
Что можно вычислить в геометрии с помощью производной?
В геометрии с помощью производной можно вычислить угловой коэффициент касательной к графику функции и найти уравнение касательной к графику функции.
Пример 1. Найти угол наклона касательной к графику функции
f(x)=х2 - 3х+1 в точке с абсциссой х=4.
Решение: f '(x)=2х-3, f '(3)=2*4-3=8-3=5;
tg α=5, α=arctg 5.
Пример 2. Составьте уравнение касательной к графику
функции f(x)=х3-2х2+5х в точке с абсциссой х0=2.
Решение: f '(x)=3x²-4х+5;
f (1)=23-2*22+5*2=8-8+10=10;
f '(1)=3*2²-4*2+5=12-8+5=9;
у=f(x0)+f '(x0)(x-x0);
у=10+9*(х-2)=10+9х-18=9х-8;
у=9х-8.
Мы рассмотрели производную с геометрической точки зрения. Из курса физики вспомним, что при движении тело имеет скорость и ускорение.
Пример 3. Тело движется прямолинейно по закону
S(t)=t3-4t2+t. Найдите скорость и ускорение тела
в момент времени t =3.
Решение: v(t)=S'(t);
a(t)=v'(t);
v(t)=3t2-8t+1;
v(3)=3*32-8*3+1=27-24+1=4м/с;
а(t)=6t-8;
а(3)=6*3-8=18-8=10м/с2.
5. Тестовая работа.
Ученикам раздаются тестовые задания. Ученики самостоятельно решают примеры.
1. Найдите производную функции: у=6х²+7х-2.
а) 2х+7; б) 12х+7; в) 2х²+7; г) 12х+7-2.
2. Вычислите производную функции: y=x⁶+cos x.
а) 6x⁵+cos x; б) 6x⁵+sin x; в) x⁵-sin x; г) 6x⁵-sin x.
3. Найдите производную функции: у=(7х+4)6.
а) 6(7х+4)5; б) 28(7х+4)5; в) 6(х+4)6; г) 42(7х+4)5.
4. Точка движется прямолинейно по закону S=3t²+4. Найдите
скорость тела в момент времени t=5.
а) 30 м/с; б) 34 м/с; в) 20 м/с; г) 24 м/с.
5.Вычислите производную функции: у=4х⁵-х4+х2-1.
а) 4х4-х³-1; б) 20х⁵-х³+2; в) 20х4-4х³+2х; г) 4х⁵-х³+2.
6.Ромашка Блума.
Ученики выбирая лепестки ромашки, отвечают на вопросы.

Как называется график функции y= sin x?
Назовите обратные тригонометрические функции к функциям у= sin x, у=cos x, у=tg x, y=ctg x.
Какой французский математик ввел термин «производная»?
Напишите общий вид решения уравнения sin х=а.
Напишите общий вид решения уравнения cos х=а.
По какой формуле вычисляют производную частного?
7. Домашнее задание:
стр. 150, №295,296.
8. Подведение итога урока. Выставление оценок.
Тестовые задания:
1. Найдите производную функции: у=6х²+7х-2.
а) 2х+7; б) 12х+7; в) 2х²+7; г) 12х+7-2.
2. Вычислите производную функции: y=x⁶+cos x.
а) 6x⁵+cos x; б) 6x⁵+sin x; в) x⁵-sin x; г) 6x⁵-sin x.
3. Найдите производную функции: у=(7х+4)6.
а) 6(7х+4)5; б) 28(7х+4)5; в) 6(х+4)6; г) 42(7х+4)5.
4. Точка движется прямолинейно по закону S=3t²+4. Найдите скорость тела в момент времени t=5.
а) 30 м/с; б) 34 м/с; в) 20 м/с; г) 24 м/с.
5.Вычислите производную функции: у=4х⁵-х4+х2-1.
а) 4х4-х³-1; б) 20х⁵-х³+2; в) 20х4-4х³+2х; г) 4х⁵-х³+2.








 Получите свидетельство
Получите свидетельство Вход
Вход



 =
= 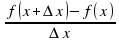 имеет предел при
имеет предел при  то этот предел называют производной функции у = f(х) в точке х.
то этот предел называют производной функции у = f(х) в точке х.

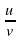 )
)




















 Конспект урока по математике «Производная функции» (0.27 MB)
Конспект урока по математике «Производная функции» (0.27 MB)
 0
0 593
593 99
99 Нравится
0
Нравится
0


