Использование нестандартных уроков
при изучении математики.
Кузьменко Е.В.,
учитель математики гимназии №10
Хотите потратить время впустую? Попробуйте доказать, что математика не нужна. Необходимость изучения этого предмета очевидна, ведь при освоении абсолютно любой дисциплины так или иначе используются математические методы. И всё же, первыми, кто часто выступает против Царицы наук и тщетно пытается доказать её бесполезность, являются дети. Школьники часто не могут запомнить теоретический материал, не всегда у них получается решать сложные задачки, поэтому со временем (а иногда даже очень быстро) у детей пропадает интерес к математике. Что же может сделать с этим учитель? Решение есть. В повседневный, ничем не примечательный учебный процесс нужно стараться включить как можно больше нестандартных занятий. Подобные уроки помогут увидеть математику в новом для учеников свете. Учитель сможет раскрыть детский потенциал, обучить школьников полезным навыкам, например, работе в группе. Кроме того, занятия нестандартного образца являются отличным способом определить уровень знаний каждого отдельного ученика, скорость решения им поставленных задач, выявить способности к творческому мышлению, лидерские качества и т.д.
Если вы хотите, чтобы ваши уроки были не испытанием для учеников, а полезным и увлекательным времяпровождением, вместе с ними откажитесь от скучного заучивания и включите в свой план нестандартные уроки!
Существует много типов нестандартных уроков. Разделим их на несколько групп:
Уроки-соревнования:
конкурсы
турниры
КВН
деловая игра
Уроки как публичные формы общения:
пресс-конференция
панорама
телепередача
Уроки, опирающиеся на фантазию
урок-сказка
урок-сюрприз
Интегрированные уроки
Изменение традиционных уроков:
парный опрос
экспресс-опрос
урок-зачёт
урок-конференция
Нестандартные уроки чаще всего проводятся как итоговые, обобщающие и закрепляющие знания, умения и навыки. Такие занятия тщательно готовятся, к их проведению привлекаются учащиеся класса, а иногда и старшеклассники. Тем не менее, нестандартные уроки не нужно проводить часто, чтобы они не стали чем-то обыденным. Это только лишь способ подогреть интерес к изучаемому предмету.
Итак, после прохождения темы для её закрепления проведём нестандартный урок. Нужно заранее предупредить детей, когда он будет, разделить их на команды и предложить им придумать по 5 вопросов для соперников. Учитель тоже придумывает вопросы, а также готовит вознаграждение за правильные ответы, чтобы вызвать больший интерес со стороны учащихся. Команды выбирают себе названия и девиз. Заранее готовятся призы для победителей, медали за лучший вопрос и лучший ответ. К этой работе можно привлечь старшеклассников, а также родителей учеников.
Возможные вопросы к уроку-зачёту по алгебре в 8 классе по теме «Уравнения».
Что называется квадратным уравнением?
Что называется полным квадратным уравнением?
Что называется неполным квадратным уравнением?
Что называется неприведённым квадратным уравнением?
Что называется приведённым квадратным уравнением?
Формулы корней квадратного уравнения.
Теорема Виета для полного неприведённого квадратного уравнения.
Теорема Виета для приведённого квадратного уравнения.
Формула разложения квадратного трёхчлена на множители.
Какое уравнение называется рациональным?
Алгоритм решения рационального уравнения.
Какое уравнение называется биквадратным?
Как решается биквадратное уравнение?
Какое уравнение называется иррациональным?
Методы решения иррационального уравнения.
Какое уравнение называется уравнением с параметрами?
Что такое посторонний корень уравнения?
Какие уравнения называются равносильными?
Какие преобразования приводят к равносильным уравнениям?
Какие преобразования приводят к неравносильным уравнениям?
Геометрия. 8 класс. Закрепление темы «Подобие треугольников».
Какие отрезки называются пропорциональными?
Что называется отношением отрезков?
Какие фигуры называются подобными?
Какие стороны называются сходственными?
Какие треугольники называются подобными?
Что называется коэффициентом подобия?
Теорема об отношении площадей подобных треугольников.
Свойство биссектрисы угла треугольника.
Свойство высот, проведённых к сходственным сторонам.
Теорема об отношении периметров подобных треугольников.
Первый признак подобия треугольников.
Второй признак подобия треугольников.
Третий признак подобия треугольников.
Практические задания к вопросам.
Проверить пропорциональны ли отрезки:
![]()
![]()
![]()
![]()
Составить отношение отрезков: а) MN и M1N1, если MN=2, M1N1=3
б) KL и K1L1, если KL=7, K1L1=3,5
Привести примеры подобных фигур.
Н
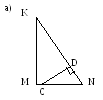 азвать сходственные стороны треугольников а)
азвать сходственные стороны треугольников а) 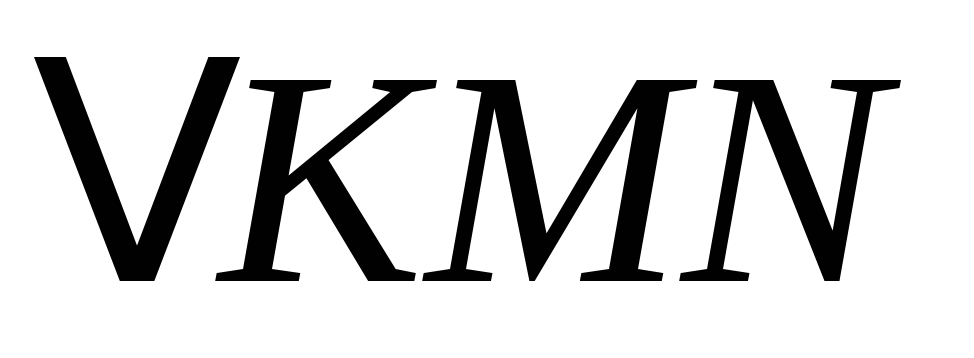 и
и 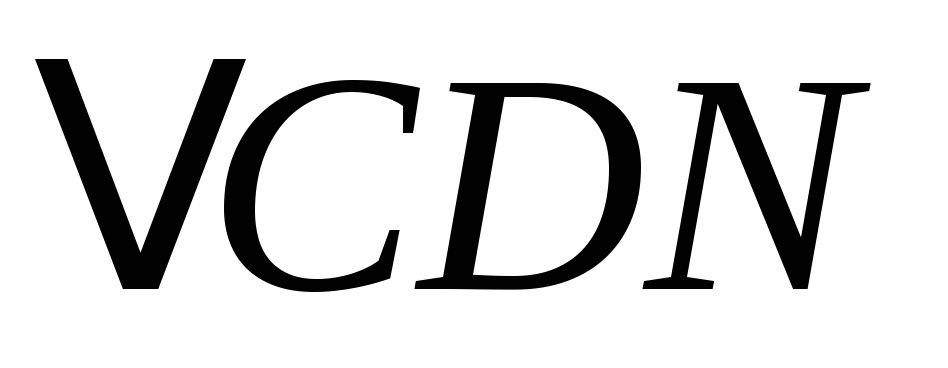
б )
) ![]() и
и ![]()
Д
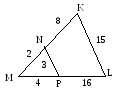 оказать, что треугольники подобны по определению:
оказать, что треугольники подобны по определению:
![]()
Используя условия предыдущей задачи, найти коэффициент подобия.
В задаче №5 найти отношение площадей треугольников MLK и MPN
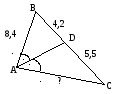
Найти АС
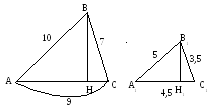
Найти отношение высот
треугольников ![]() и
и ![]()
а) ![]() ; б)
; б) ![]() ; в)
; в) 
где BH, B1H1, AK, A1K1, CM, C1M1-высоты
В задаче №5 найти отношение периметров треугольников.
Диагонали трапеции ABCD с основаниями AD и BC пересекаются в точке О. Периметры треугольников BOC и AOD относятся, как 2:3. AC=20. Найти AO, OC.
Прямая, параллельная стороне MN
 MNK, пересекает стороны KM и KN в точках E и F соответственно, КЕ=6см, КМ=10см, KF=9см, KN=15см.
MNK, пересекает стороны KM и KN в точках E и F соответственно, КЕ=6см, КМ=10см, KF=9см, KN=15см.
Найти отношения: а) EF:MN
б) периметров ![]() KMN и
KMN и ![]() KEF
KEF
в) площадей ![]() KEF и
KEF и ![]() KMN
KMN

 Получите свидетельство
Получите свидетельство Вход
Вход











 Нестандартные уроки (96 KB)
Нестандартные уроки (96 KB)
 0
0 686
686 28
28 Нравится
1
Нравится
1







