Неравенство треугольника. 7 класс.

Урок геометрии в 7 классе.

Тема урока: Неравенство треугольника

Санкт - Петербург

2022

Цели урока: 1. Доказать теорему о соотношении между сторонами и углами треугольника, следствия из этой теоремы; 2. Научиться применять эти знания при решении задач; 3. Продолжить развитие геометрической интуиции; 4.Повысить мотивацию к изучаемому предмету. Задачи: знать –теорему о соотношении между сторонами и углами треугольника, следствия из этой теоремы; уметь – вести исследование с опорой на изученную теорему.

Ход урока:

• Организационный момент.
• Решение подготовительной задачи.
• Доказательство первого утверждения теоремы.
• Устно решить задачу № 236.
• Доказательство обратного утверждения.
• Устно решить задачу № 237.
• Доказательство следствий 1 и 2. Закрепление изученного материала (решение задач по готовым чертежам (№ 239)).
• Подведение итогов урока.

L 3; 2) L МОС L 3. О 1 Доказательство : 3 2 М К С " width="640"

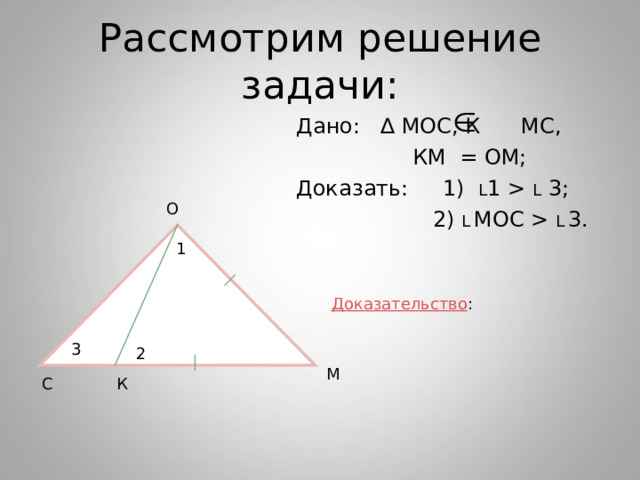
Рассмотрим решение задачи:

Дано: ∆ МОС, К МС,

КМ = ОМ;

Доказать: 1) L 1 L 3;

2) L МОС L 3.

О

1

Доказательство :

3

2

М

К

С

АС. Доказать: L С L В. B A " width="640"

Теорема о соотношении между сторонами и углами треугольника:

В треугольнике против большей стороны лежит больший угол.

С

Дано: ∆ АВС, АВАС.

Доказать: L С L В.

B

A

L 1. L 2 – внешний угол ∆ ВС D , поэтому L 2 L В. L 1 = L 2, как углы при основании равнобедренного ∆ А D С. Таким образом, L С L 1 , L 1= L 2, L 2 L В. Отсюда следует, что L С L В. Теорема доказана. " width="640"

Доказательство:

Отложим на стороне АВ

отрезок равный стороне

АС. Так как А D

А- D -В , L 1 – часть L С и ,

значит L С L 1.

L 2 – внешний угол ∆ ВС D ,

поэтому L 2 L В.

L 1 = L 2, как углы при

основании равнобедренного

∆ А D С. Таким образом,

L С L 1 , L 1= L 2, L 2 L В.

Отсюда следует, что L С L В.

Теорема доказана.

ВСАС; б) АВ=АС" width="640"

Решить задачу:

№ 236.

Сравните углы треугольника АВС и выясните, может ли быть угол А тупым, если:

а) АВВСАС;

б) АВ=АС

АС Доказать (заключение) L АСВ L АВС ∆ АВС, L АСВ L АВС АВАС " width="640"

Прямая и обратная теоремы о соотношениях между сторонам и углами треугольника

Теорема

Дано

(условие)

Обратная теорема

∆ АВС, АВАС

Доказать

(заключение)

L АСВ L АВС

∆ АВС,

L АСВ L АВС

АВАС

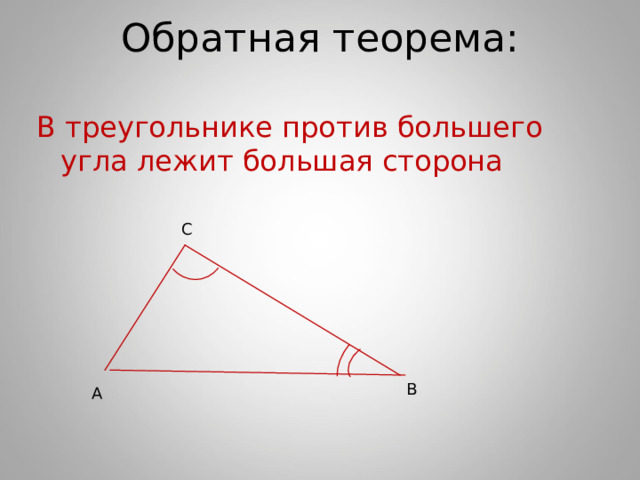
Обратная теорема:

В треугольнике против большего угла лежит большая сторона

C

B

A

L В. Доказать: АВ АС. Доказательство: Методом от противного. С В А " width="640"

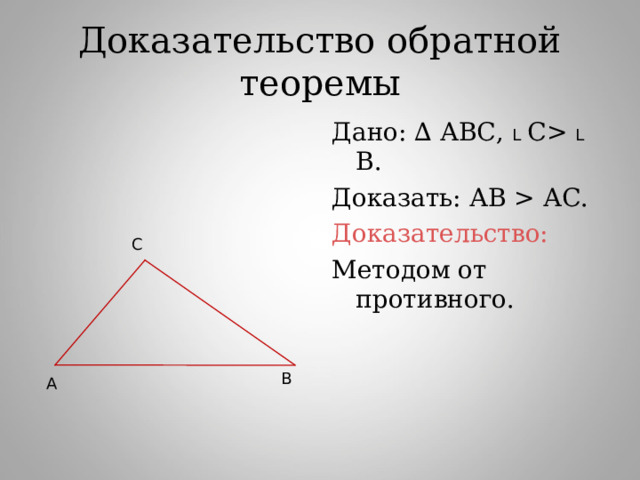
Доказательство обратной теоремы

Дано: ∆ АВС, L С L В.

Доказать: АВ АС.

Доказательство:

Методом от противного.

С

В

А

L В L С; б) L А L В = L С. " width="640"

Решить задачу № 237 (устно)

Сравните стороны треугольника АВС, если:

а) L А L В L С;

б) L А L В = L С.

Следствие 1.

В прямоугольном

треугольнике гипотенуза

больше катета.

А

В

С

Решить задачу № 239 .

Докажите, что в треугольнике медиана не меньше высоты, проведённой из той же вершины.

Следствие 2.

Если два угла одного

треугольника равны,

то треугольник

равнобедренный

(признак

равнобедренного

треугольника).

(Доказать методом от противного.)

С

В

А

Решите задачу № 240 .

В равнобедренном треугольнике АВС с основанием АС биссектрисы углов А и С пересекаются в точке О. Докажите, что треугольник АОС - равнобедренный.

В

N

H

О

А

С

Итог урока.

• Изучена теорема о соотношениях

между сторонами и углами

треугольника.

2. Изучены следствия из теоремы о

соотношениях между сторонами и

углами треугольника.

Домашнее задание: п. 32, № 238, ( 240 ) .

До новых встреч!