Непрерывная дробь

Непрерывные дроби

22 Июнь 2011, 0:05

Исторически непрерывные, или цепные дроби появились в связи с необходимости найти наилучшее приближение вещественного числа с помощью числа рационального. Так, при конструировании зубчатых передач для передачи вращения с одного колеса на другое требуется нарезать на одном из них зубцов, а на другом — , так чтобы отношение как можно лучше приближало заранее заданное отношение угловых скоростей . При этом ясно, что чем меньше зубцов нужно будет нарезать, тем это будет выгоднее. Интересно, что к такой же задаче сводится и установление длины года — ведь Земля совершает оборот вокруг Солнца за суток, а это число иррациональное. Давайте же посмотрим, что такое цепные дроби и как они связаны с алгоритмом Евклида нахождения наибольшего общего делителя двух чисел.

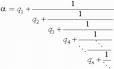
Определение. Непрерывной (или цепной) дробью называется выражение вида

Непрерывная дробь может быть как конечной, так и бесконечной.

Числа , участвующие в разложении числа в непрерывную дробь, называются неполными частными.

Иногда непрерывную дробь обозначают следующим образом (с помощью неполных частных): .

Возьмем произвольное вещественное число . Пусть — целая часть числа ( — наибольшее целое число, не превосходящее ). Если число не целое, то получим . Если не является целым числом, то для него также можно найти целую часть и найти число и т.д.:

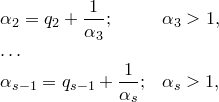
откуда и получаем разложение в непрерывную дробь:

Ясно, что если число иррационально, то непрерывная дробь будет бесконечной. Действительно, любая конечная цепная дробь является рациональным числом.

Пример 1. Разложим в непрерывную дробь число .

, поэтому

, следовательно,

поэтому

т.е. . Следовательно, неполные частные также будут повторяться. И разложение в непрерывную дробь имеет вид

Если же число рационально, то оно представимо конечной непрерывной дробью. Разложить в непрерывную дробь в этом случае можно с помощью алгоритма Евклида.

Отсюда последовательной заменой каждой дроби

на ее соответствующее выражение, получается представление

Определение. Дроби

называются подходящими дробями.

Теорема. Для подходящих дробей при справедливо соотношение

Другими словами, числители и знаменатели подходящих дробей можно последовательно находить по формулам

Доказательство. Доказывать будем по индукции. Проверим базу индукции. Положим , . Тогда поскольку получается из заменой в выражении для числа на , имеем

Предположим теперь, что справедливо равенство

Тогда

Тем самым, для справедливо равенство того же вида. Теорема доказана.

Вычисления и удобно производить с помощью следующей таблицы:

Замечание. Последний столбец пишем только в том случае, когда — несократимая дробь с положительным знаменателем: .

Пример 2. Разложим в непрерывную дробь несократимую дробь :

Получаем непрерывную дробь:

Таблица выглядит следующим образом:

Таким образом, подходящие дроби будут следующие:

В случае же, когда числитель и знаменатель дроби не взаимно простые (НОД) в последнем столбце таблицы будут стоять числитель и знаменатель несократимой дроби, равной данной дроби .

Пример 3. Разложим в непрерывную дробь :

Утверждение 1. 1) При имеем

2) При имеем

Доказательство. Действительно, при получаем

Далее из равенств

откуда сразу же следует требуемое.

Вторая часть утверждения получается следующим образом:

Следствие. Линейное представление наибольшего общего делителя чисел и получается из равенства

домножением на НОД, поскольку .

Пример 4. Приведем линейное представление наибольшего общего делителя чисел и (см. пример 3):

или

Утверждение 2. Пусть , а если — рациональная несократимая дробь с положительным знаменателем, то пусть также . Тогда лежит между и , причем ближе к , чем к .

Доказательство. Заменим в равенстве

на , получим

откуда ясно, что первая из разностей, стоящих в скобках, по знаку противоположна второй и численно меньше (так как ), что и доказывает наше утверждение.