| Мұғалімнің аты-жөні: | Тайжанова Алтынкыз Канатовна | |
| Күні: | 21.12.16 | |
| Сынып: | 8 «A» | |
| Пәні: | Геометрия | |
| Тақырыбы: | Негізгі тригонометриялық тепе-теңдіктер және оның салдары | |
| Негізгі түйінді идея: | Негізгі тригонометриялық теңбе – теңдіктерді өрнектейтін формулаларды білу, өрнектерді ықшамдауда, теңбе – теңдіктерді дәлелдеуде қолдана білу | |
| Оқу мақсаты: | Негізгі тригонометриялық теңбе – теңдіктерді өрнектейтін формулаларды білу, өрнектерді ықшамдауда, теңбе – теңдіктерді дәлелдеуде қолдана білу | |
| Табыс критерийлері | ||
| Барлық оқушылар: Негізгі тригонометриялық теңбе – теңдіктерді өрнектейтін формулаларды білу | Көпшілік оқушылар: Негізгі тригонометриялық теңбе – теңдіктерді өрнектейтін формулаларды білу, | Жекелеген оқушылар: өрнектерді ықшамдауда, теңбе – теңдіктерді дәлелдеуде қолдана білу |
| Кезеңдер | уақыт | Мұғалімнің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар | ||||||||
| 2цНегізгі бөлім | I. Қызығушы-лығын ояту | 2 мин | α сүйір бұрышының әрбір мәніне сәйкес sinα-ның, cosα-ның, tgα-ның және ctgα-ның мәндерін анықтауға болады. 1. Катеттері а мен b, гипотенузасы с болатын, ал сүйір бұрыштары α мен β-ға тең АВС тік бұрышты үшбұрышы берілсін. Пифагор теоремасын жазамыз: a2+b2=c2 (*) §8, (1) және (2) формулалардан b=ccosα, a=csinα болатыны белгілі. Осы мәндерді (*) –ға қойсақ, sin2α+cos2α=1 (1) шығады. Бұл α бұрышының синусы мен косинусын байланыстыратын теңбе-теңдік. | Марапат арқылы бағалау | Сызғыш, оқу дәптері, оқулық | ||||||||
| II.Мағына-ны тану кезеңі |
3 мин | Негізгі тригонометриялық теңбе-теңдіктер 2. Берілген тікбұрышты үшбұрыш үшін болатыны белгілі. Бұл теңдіктерге b=ccosα, a=csinα мәндерін қойсақ, Аламыз. Бұл теңдіктер кез-келген α сүйір бұрышы үшін орындалатын теңбе-теңдік болып саналады. 3. (1) тепе-теңдік әрбір мүшесін сos2α-ға немесе sin2α-ға бөліп, төмендегідей екі тепе-теңдікті алуға болады: 1+tg2α= 1+ctg2α= 4. АВС тікбұрышты үшбұрышына сүйір бұрыштар үшін α+β=900 өрнегі Бұдан β=900-α. 30-суреттен sin= cos(900-α) =sinα (6) теңбе-теңдігін аламыз. Осы сияқты sin(900-α)=cosα (7) теңбе-теңдігін алуға болады. | Марапат арқылы бағалау | Сызғыш, оқу дәптері, оқулық | |||||||||
| III.Ой толғаныс кезеңі |
28 мин | №144. Өрнекті ықшамдаңдар 2+sin2α+cos2α=2+1=3 (1 – sinα )(1+sinα)=1-sin2α=cos2α
№145. (1+ctg2α)∙sin2α+1= tgα∙ctgα+sinα=1+sinα
| №286 Өрнекті ықшамдаңдар
№287
|
| Сызғыш, оқу дәптері, оқулық | ||||||||
| Қорытынды бөлім | 1 мин | Үйге №146 |
|
| |||||||||
| 1 мин | Рефлексия. Қол көтеру арқылы |
|
| ||||||||||
|
| 1 мин | Бағалау. Жиынтық баға қою |
|
| |||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



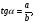 ctgα=
ctgα=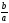
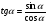 (2)
(2)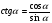 (3)
(3)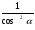 (4)
(4)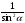 (5)
(5)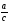 , ал cosβ=
, ал cosβ=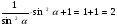









 Негізгі тригонометриялық тепе-теңдіктер және олардың салдары (27.64 KB)
Негізгі тригонометриялық тепе-теңдіктер және олардың салдары (27.64 KB)
 0
0 1280
1280 45
45 Нравится
0
Нравится
0



