Неравенства

Презентация состоит из 53 слайдов.

Пример 1

Доказать неравенство (a-3)(a-5)<(a-4)2;

Составим разность (a-3)(a-5)-(a-4)2  = a2 -3a-5a+15-a2+8a-16= -1<0. Неравенство верно.

Пример 2

Доказать неравенство a2 + b2 ≥ 2ab ;

Составим разность a2 + b2 - 2ab = (a-b)2 ≥ 0.

Неравенство верно.

Расположите в порядке возрастания числа a, b и c,

 если a-b<0; c-b>0.

Решение.

a-b<0, значит a

c-b>0, значит c>b.

Имеем a

Ответ: a, b, c.

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

Теорема 1.

Если a>b, то b

Доказательство. 

Действительно, если a-b>0,то b-a<0.

Теорема 2

Если a

Доказательство. 

Докажем, что a-c<0.

a-c=a-c+b-b=(a-b)+(b-c)<0

Аналогично, если a>b и b>c, то a>c.

Теорема 3

Если a

Доказательство. 

Составим разность. (a+c)-(b+c) = a-b<0.

Учитель Козина Н.А.

НЕРАВЕНСТВА

17 января 2011Г

Учитель Козина Н.А.

ЧИСЛОВЫЕ НЕРАВЕНСТВА

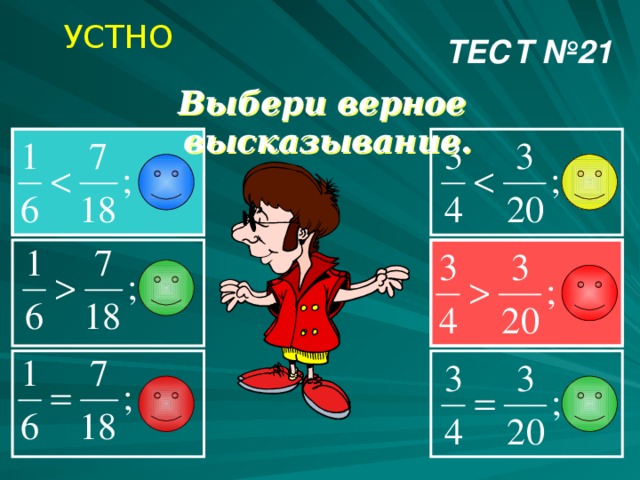
УСТНО

ТЕСТ №21

Выбери верное высказывание.

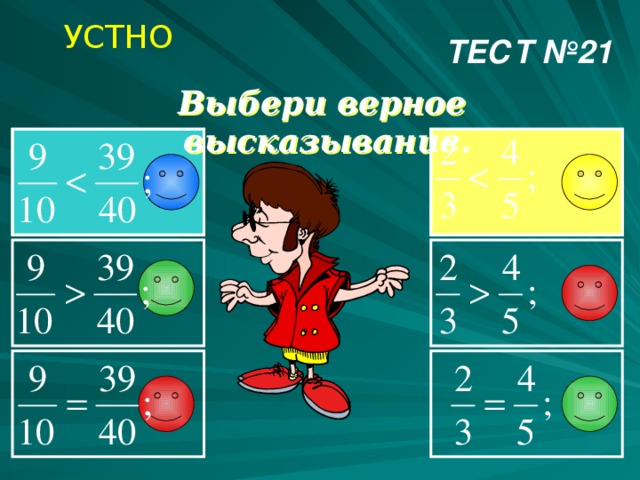
УСТНО

ТЕСТ №21

Выбери верное высказывание.

№ 1

Сравните числа

№ 1

Сравните числа

b, если a – b 0; a a = b, если a – b = 0. УСТНО № 724 " width="640"

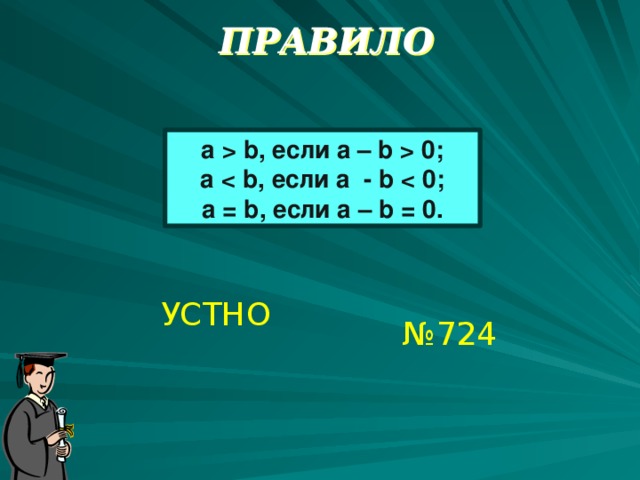
ПРАВИЛО

a b, если a – b 0;

a

a = b, если a – b = 0.

УСТНО

№ 724

ДОКАЗАТЕЛЬСТВО

НЕРАВЕНСТВ

Пример 1

Доказать неравенство (a-3)(a-5)

Составим разность (a-3)(a-5)-(a-4) 2 =

a 2 -3a-5a+15-a 2 +8a-16=

= -1

Пример 2

Доказать неравенство a 2 + b 2 ≥ 2ab ;

Составим разность a 2 + b 2 - 2ab = (a-b) 2 ≥ 0.

Неравенство верно.

№ 728 б,г

№ 731 б,г

№ 734

Математический

диктант

Записать только числовое выражение.

• № 1а Сравните числа a и b ,
• если a - b = -2.

Записать только числовое выражение.

• № 1б Сравните числа a и b ,
• если a - b = .

Записать только числовое выражение.

• № 2 Сравните числа

Записать только числовое выражение.

• № 3 Докажите неравенство
• x 2 -2x + 1 ≥ 0

0 " width="640"

Записать только числовое выражение.

• № 4 При каких значениях переменной верно неравенство │x│ 0

b 2) " width="640"

Ответы.

• 3) (x-1) 2 ≥ 0

• 4) x ≠ 0

• 1а) a

• 1б) ab

• 2)

0, значит cb. Имеем aОтвет: a, b, c. " width="640"

№ 3

Расположите в порядке возрастания числа

a, b и c,

если a-b0.

Решение.

a-b

c-b0, значит cb.

Имеем a

Ответ: a, b, c.

n. Расположите в порядке убывания числа m+1, n-5, n. Решение. mn; m+1m, значит m+1n; nn-5. Имеем m+1nn-5. Ответ: m+1, n, n-5. " width="640"

№ 4

Известно, что mn.

Расположите в порядке убывания числа

m+1, n-5, n.

Решение.

mn;

m+1m, значит m+1n;

nn-5.

Имеем m+1nn-5.

Ответ: m+1, n, n-5.

дома

П28 правило

№ 725, 729а,в, 735а,б, 744.

18 января 2011Г

Учитель Козина Н.А.

СВОЙСТВА

ЧИСЛОВЫХ НЕРАВЕНСТВ

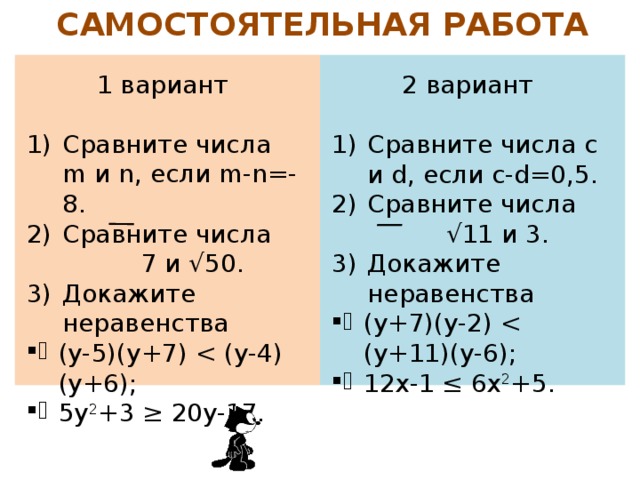
САМОСТОЯТЕЛЬНАЯ РАБОТА

1 вариант

2 вариант

• Сравните числа m и n, если m-n=-8.
• Сравните числа 7 и √50.
• Докажите неравенства

• Сравните числа c и d, если c-d=0,5.
• Сравните числа √11 и 3.
• Докажите неравенства

• (y-5)(y+7)
• 5y 2 +3 ≥ 20y-17.

• (y+7)(y-2)
• 12x-1 ≤ 6x 2 +5.

b, то bДоказательство. Действительно, если a-b0,то b-aТЕОРЕМА 2 Если aДоказательство. Докажем, что a-ca-c=a-c+b-b=(a-b)+(b-c)c b a c b a Аналогично, если ab и bc, то ac. " width="640"

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

ТЕОРЕМА 1

Если ab, то b

Доказательство.

Действительно, если a-b0,то b-a

ТЕОРЕМА 2

Если a

Доказательство.

Докажем, что a-c

a-c=a-c+b-b=(a-b)+(b-c)

c

b

a

c

b

a

Аналогично, если ab и bc, то ac.

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

ТЕОРЕМА 3

Если a

Доказательство.

Составим разность. (a+c)-(b+c) = a-b

ПРАВИЛО СТР157

ЕСЛИ К ОБЕИМ ЧАСТЯМ ВЕРНОГО НЕРАВЕНСТВА ПРИБАВИТЬ ОДНО И ТО ЖЕ ЧИСЛО, ТО ПОЛУЧИТСЯ ВЕРНОЕ НЕРАВЕНСТВО.

0 0 ПРАВИЛО СТР158 " width="640"

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

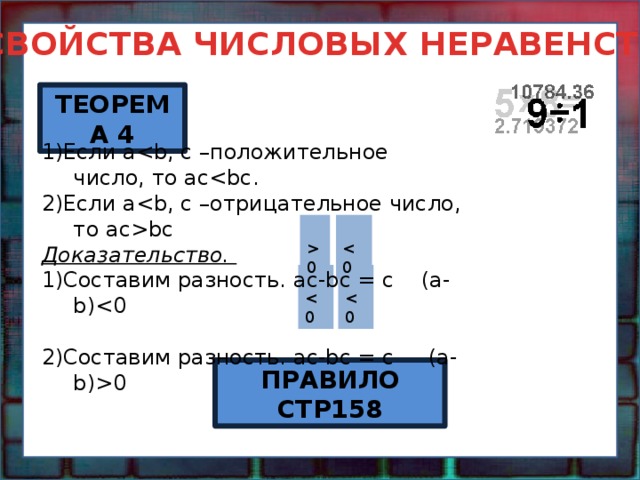
ТЕОРЕМА 4

1)Если a

2)Если abс

Доказательство.

1)Составим разность. ac-bc = c (a-b)

2)Составим разность. ac-bc = c (a-b)0

0

ПРАВИЛО СТР158

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

ТЕОРЕМА 4

1)Если a

2)Если abс

ПРАВИЛО

ЕСЛИ ОБЕ ЧАСТИ ВЕРНОГО НЕРАВЕНСТВА УМНОЖИТЬ ИЛИ РАЗДЕЛИТЬ НА ОДНО И ТО ЖЕ ПОЛОЖИТЕЛЬНОЕ ЧИСЛО, ТО ПОЛУЧИТСЯ ВЕРНОЕ НЕРАВЕНСТВО;

ЕСЛИ ОБЕ ЧАСТИ ВЕРНОГО НЕРАВЕНСТВА УМНОЖИТЬ ИЛИ РАЗДЕЛИТЬ НА ОДНО И ТО ЖЕ ОТРИЦАТЕЛЬНОЕ ЧИСЛО И ИЗМЕНИТЬ ЗНАК НЕРАВЕНСТВА НА ПРОТИВОПОЛОЖНЫЙ, ТО ПОЛУЧИТСЯ ВЕРНОЕ НЕРАВЕНСТВО.

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

№ 746

№ 748

№ 750

№ 752

№ 753

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

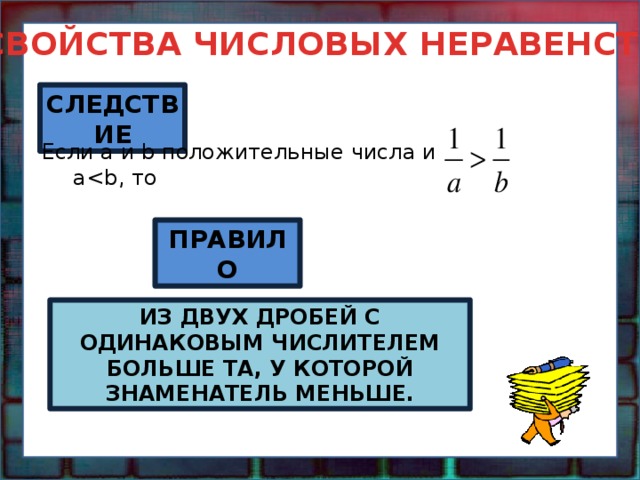
СЛЕДСТВИЕ

Если a и b положительные числа и a

Доказательство.

Разделим обе части неравенства a

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

СЛЕДСТВИЕ

Если a и b положительные числа и a

ПРАВИЛО

ИЗ ДВУХ ДРОБЕЙ С ОДИНАКОВЫМ ЧИСЛИТЕЛЕМ БОЛЬШЕ ТА, У КОТОРОЙ ЗНАМЕНАТЕЛЬ МЕНЬШЕ.

b, da. Расположите в порядке возрастания числа Решение. Сравним a, b, c и d. Имеем: dЗначит: a d b c " width="640"

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

СЛЕДСТВИЕ

№ 755

Если a, b, с и d - положительные числа и

ab, da.

Расположите в порядке возрастания числа

Решение.

Сравним a, b, c и d.

Имеем: d

Значит:

a

d

b

c

СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ

№ 757

№ 759

№ 761

ДОМАШНЕЕ ЗАДАНИЕ

П29 ПРАВИЛА

№ 747

№ 749

№ 751

№ 758

№ 756

20 января 2011Г

Учитель Козина Н.А.

СЛОЖЕНИЕ И УМНОЖЕНИЕ

ЧИСЛОВЫХ НЕРАВЕНСТВ

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

№ 1

• a

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

№ 2

• m

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

№ 3

• 5
• x-3
• -x
• 2x-12

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

ответы

• 1)
• 2)
• 3) 5
• 2
• -6
• -2

Сложение и умножение

Числовых неравенств

ТЕОРЕМА 5

Если a

Доказательство.

Прибавим к обеим частям неравенства a

a+c

Прибавим к обеим частям неравенства c

c+b

Имеем: a+c

ПРАВИЛО СТР161

Сложение и умножение

Числовых неравенств

ТЕОРЕМА 5

Если a

ПРАВИЛО СТР161

ЕСЛИ ПОЛЧЛЕННО СЛОЖИТЬ ВЕРНЫЕ НЕРАВЕНСТВА ОДНОГО ЗНАКА, ТО ПОЛУЧИТСЯ ВЕРНОЕ НЕРАВЕНСТВО

Сложение и умножение

Числовых неравенств

ТЕОРЕМА 6

ПРАВИЛО СТР161

Если a

Доказательство.

Умножим обе части неравенства a

ac

Умножим обе части неравенства c

сb

Имеем: ac

Сложение и умножение

Числовых неравенств

ТЕОРЕМА 6

ПРАВИЛО СТР161

Если a

ЕСЛИ ПОЧЛЕННО ПЕРЕМНОЖИТЬ ВЕРНЫЕ НЕРАВЕНСТВА ОДНОГО ЗНАКА, ЛЕВЫЕ И ПРАВЫЕ ЧАСТИ КОТОРЫХ – ПОЛОЖИТЕЛЬНЫЕ ЧИСЛА, ТО ПОЛУЧИТСЯ ВЕРНОЕ НЕРАВЕНСТВО.

Сложение и умножение

Числовых неравенств

ПРИМЕР

15

Оценить x+y, x-y, xy,

Оценим x+y

15

2

17

Оценим x-y

2

-3

Оценим xy

15

-3

12

15

2

30

Сложение и умножение

Числовых неравенств

ПРИМЕР

15

Оценить x+y, x-y, xy,

Оценим

15

2

Сложение и умножение

Числовых неравенств

ДОМА

П29 ПРАВИЛА №769, 771, 764в,г, 916а,в.

21 января 2011Г

Учитель Козина Н.А.

СЛОЖЕНИЕ И УМНОЖЕНИЕ

ЧИСЛОВЫХ НЕРАВЕНСТВ

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• № 1 x
• Сравните
• а)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• x
• Сравните
• б) 2,07x и 2,07y

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• x
• Сравните
• в)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• x
• Сравните
• г)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• № 2
• Оцените
• а)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• № 2
• Оцените
• а)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• № 2
• Оцените
• а)

МАТЕМАТИЧЕСКИЙ ДИКТАНТ

• № 3 Ширина 2
• Длина 4
• Оцените периметр и площадь прямоугольника.