Оглавление
Аннотация ___________________________________________________________3
Введение ___________________________________________________________4-5
Глава 1. Теоретическая часть. Из истоии математики измерения площадей и периметров
1.1 Как измеряли в древности__________________________________________6-7
1.2 Единицы измерения в древние времена_______________________________7-8
1.3 Единицы измерения в настоящее время______________________________8-9
Глава 2. Практическая часть. Использование математических знаний при ремонте
2.1 Планирование проекта __________________________________________10-11
2. 2 Анкетирование с целью выявления значимости выбранной темы ______11-14
2.3 Математические расчеты по выполнению ремонтных затрат___________14-17
Обзор литературных источников________________________________________18
Результаты и выводы__________________________________________________19
Список использованных литературных источников_________________________20
Приложение
Аннотация
Вработе дается ответ на вопрос : «Действительно ли математика играет важную роль при ремонте помещения?» Приведены необходимые математические расчеты, для выполнения косметического ремонта детской комнаты.
« Если вы хотите участвовать в большой жизни, то наполните свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь в вашей работе»
М.И.Калинин.
Введение
В жизни невозможно встретить ни одного человека, который не занимался бы математикой. Каждый из нас умеет считать, умножения, умеет строить геометрические фигуры
По улице движутся автомобили. Их колёса - круги. Сядем в поезд. Станция далеко позади. Но и здесь геометрия не покидает нас. Вдоль дороги на столбах натянуты провода - это прямые линии, а столбы - это перпендикуляры к земле. Вот линия высоковольтной передачи, провода от собственной тяжести слегка провисают к земле, а зимой же они, наоборот, натягиваются, так как металл от холода сжимается. Вопросом определения необходимой длины такого провода для передачи на большие расстояния занимается математика.
Кто-то из нас, возможно, думает, что различные замысловатые линии и поверхности можно встретить только в книгах учёных математиков. Однако это не так. Стоит внимательно присмотреться, и мы сразу обнаружим вокруг нас всевозможные геометрические фигуры. Оказывается, их очень много, просто раньше мы их не замечали. Вот комната. Все её стены, пол и потолок являются прямоугольниками, а сама комната - параллелепипедом.
Проблемный вопрос: Для чего при планировании косметического ремонта может пригодиться знание математики?
Гипотеза исследования состоит в том, что если точно высчитать все измерения комнаты, то можно купить определенное количество строительного материала, тем самым сэкономить семейный бюджет
Актуальность работы заключается в том, что ремонт помещения был, есть и будет необходим всегда, поэтому необходимо научиться расчитывать его с наиболее меньшим количеством затраченных средств
Цель работы: научиться делать расчеты при выполнении ремонтных работ для закупки необходимого количества строительных материалов
Задачи работы:
- узнать, как измеряли в древности и в настоящее время; изучить какие единицы измерения длины и площади использовали наши предки; закрепить понятия периметра и площади;
- показать необходимость математических знаний при расчете ремонта помещения
Объектом исследования является спальная комната
Предметом математического исследования являются понятия: площадь и периметр, расчеты стоимости товара
В ходе исследования использовались различные методы и приемы анализа учебной и научно-популярной литературы, ресурсов сети Интернет, социологический опрос, практическая работа.
Глава 1. Из истории математики измерения площади и периметра
1.1 Как измеряли в древности
Жизненные потребности заставили человека измерять уже в древности расстояния, а также площадь. Человек хотел знать измерения своего земельного участка, жилища и т.д. Из вышеуказанной потребности возникла наука «геометрия» («гео» - земля, «метрио» - мерить). “Измерялись площади земельных участков, емкость сосудов и амбаров, объем вынутой при земельных работах земли. Мы знаем из сохранившихся клинописных записей вавилонян, что единицы измерения площади и объема, были при своем возникновении связаны с материальными потребностями общества.
Зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий.
В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон.
Египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция.
Около 4 000 лет назад египтяне определяли площадь прямоугольника, теми же приемами, как и мы. То есть, чтобы определить площадь прямоугольника, умножали длину на ширину.
Египтяне использовали и иные приемы, которые позволяли быстрее измерять площадь земельного участка путем только обхода его по границам, но результат измерения получался с некоторой погрешностью. Единицей измерения площади издревле использовали квадрат.
У вавилонян не было таких геометрических понятий как точка, прямая, линия, плоскость, параллельность. Измерение производилось при помощи веревки. Геометрические познания вавилонян превышали египетские.
Какими единицами измеряли площадь в древние времена?
Человек столкнулся с необходимостью измерений в глубокой древности, на раннем этапе своего развития – в практической жизни, в земледелии, строительстве своего жилья, дворцов своих властителей, храмов, в торговле. Людям потребовалось измерять расстояния, площади, объемы, веса, и, разумеется, время.
1.2 Единицы измерения в древние времена
В древности существовало множество способов измерить длину. Измеряли всем, что попадалось человеку под руки и с помощью всего, что люди видели вокруг, а также с помощью своего тела (в основном используя конечности).
Бамбуковая палочка. В Древнем Китае единицей длины служила бамбуковая палочка, издававшая при свисте звук определенной высоты.
Бычьи рога. В Сибири в древности употреблялась мера длины бука. Это расстояние, на котором человек перестает видеть рога быка.
Бычий рев. Эта мера земельной площади часто использовалась в древние времена и соответствовала размерам участка, в пределах которого был отчетливо слышен рев быка.
Солнце. В древности человек с первыми лучами солнца шел навстречу светилу, пока оно полностью не поднималось над горизонтом. Пройденное за это время расстояние называлось «стадией».
Зерно. Английский дюйм (сейчас равен 2,54 см) первоначально определялся как длина трех пшеничных зерен, взятых из середины колоса.
Связанные с размерами частей тела человека
Шаг. Древнейшая мера длины, равная средней длине шага человека — 71 см.
«Миля» происходит от латинского «тысяча». У римлян так называлось расстояние, равное 1000 двойных шагов легионера.
Ступня. Английская единица длины фут (от foot — ступня) определялась как «длина королевской ступни». Современный фут равен 30,48 см.
Пальцы. Старорусский «вершок» (примерно 4,5 см) изначально равнялся длине основной фаланги указательного пальца. «Сажень» - расстоянию от конца пальцев одной руки до конца пальцев другой (152 см).
Локоть (расстояние от локтевого сустава до вытянутого среднего пальца) служил единицей измерения у многих народов. В Древнем Египте существовал так называемый «царский локоть». Величина этой древнейшей меры длины, по разным источникам, составляла от 38 до 47 см.
Аршин (от персидского «арш» — локоть) — в древнерусской системе мер означал длину всей вытянутой руки от плеча до кончика среднего пальца (45,5 – 47,5см). Купцы, продавая товар, пользовались своим «аршином» (линейкой) или быстро отмеряли от плеча — как правило, не в пользу покупателя. Чтобы исключить обман, во времена Петра I ввели «казенный аршин» (около 72 см), который представлял собой деревянную линейку с государственным клеймом.
Для измерения площади у русского народа были свои особые мерки: копна, выть, соха, обжа, коробь, веревка, жеребья. От древних землемеров нам досталось только само слово “площадь”.
Единицы измерения в настоящее время
Как мы смогли убедиться, в древности длину измеряли чем угодно, как попало и кто во что горазд, но бурное развитие международных отношений настоятельно требовало единых для всех единиц измерения. И вот, во второй половине 18 века ученые Французской академии наук разработали общую для всего мира единицу измерения длины – Метр.
1.3 Единицы измерения в настоящее время
Метр определили как одну сорокамиллионную (1/40 000 000) часть меридиана, который проходит через Париж.
До 1960 года меру длины сверяли с этим бруском. Он и до сих пор хранится в Международном бюро мер и весов в городе Севр (предместье Парижа), но по назначению уже не используется.
Поэтому для простоты и удобства было решено: метром считать длину пути, которую в вакууме проходит свет за 1/299 792 458 секунды. Эта величина и является эталоном метра на сегодняшний день!
Гектар - метрическая единица площади, равная площади квадрата со стороной 100 м: 1 га = 10000 м². Понятие «гектар» было введено в практику после Октябрьской революции, вместо десятины, которая имела соотношение 1 га = 11/12 десятины.
Единицы измерения площадей
| 1 см2 = 100 мм2 | 1 а = 100 м2 |
| 1 дм2 = 100 см2 | 1 га = 10 000 м2 = 1000 а |
| 1 м2 = 100 дм2 = 1000 см2 | 1 км2=100 га = 100 000 м2 |
Площадь квартиры, комнаты измеряют в м2; площадь земельного участка в сотках, гектарах.
Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры.
Чтобы измерить площадь фигуры, нужно иметь единицу площади. Такой единицей сейчас, как и в древности является площадь квадрата со стороной, равной единичному отрезку. Число, которое получается в результате измерения площади фигуры, называют численным значением площади фигуры при выбранной единице площади . Оно должно удовлетворять условиям:
1) Число - положительное.
2) Если фигуры равны, то равны численные значения их площадей.
3) Если фигура состоит из фигур, то численное значение площади фигуры равно сумме численных значений площадей фигур.
4) При замене единицы площади численное значение площади данной фигуры увеличивается (уменьшается) во столько же раз, во сколько новая единица меньше (больше) старой.
5) Численное значение площади единичного квадрата принимается равным 1.
6) Если фигура является частью фигуры, то численное значение площади фигуры не больше численного значения площади фигуры
Глава 2. Практическая часть. Использование математических знаний при ремонте
2.1 Планирование проета
Казалось бы, что общего между этими понятиями? При планировании ремонта надо профессионально составить смету, чтобы уложиться в бюджет. Строгие правила математики здесь очень помогают(Приложение «фото 1», «фото 2», «фото 3»).
Кроме того, стройка и ремонт, как и математика, активно развивают мозги, учат находить оптимальное решение в нестандартных задачах (как при весьма ограниченном бюджете, осуществить все задуманные идеи).
План по осуществлению проекта
| Дата | Выполняемая работа | Необходимые материалы |
| Сентябрь, 2014 | Анкетирование | Блокнот, ручка, компьютер |
| Сентябрь,2014г. | 1)Измерение площади поверхностей комнаты (потолок, стены и пол) | Рулетка, тетрадь, ручка |
| Сентябрь, 2014г | Расчет площадей комнаты | Тетрадь, ручка |
| Сентябрь, 2014г. | Консультация с родителями по выбору материалов для ремонта | Тетрадь, ручка |
| Октябрь, 2014г. | Поиск материалов и их стоимость с использованием интернета и посещение строительных баз и магазинов на территории микрорайона | Компьютер, тетрадь, ручка |
| Октябрь, 2014г | Составление сметы расходов для ремонта | Тетрадь, ручка |
| Октябрь-ноябрь, 2014г | Ремонтные работы в комнате | Строительные материалы |
Каждое жилое помещение обязательно сталкивается с проблемой ремонта. И тогда возникает ряд вопросов : Какой выбрать дизайн, сколько и где надо закупить необходимого материала, где это можно сделать дешевле и т.д. А самый важный вопрос: как все сделать так, чтобы всем обитателем этого помещения было удобно и комфортно? Возможно несколько вариантов:
1.Полностью доверить работу специалистам, говорят « под ключ»;
2.Самим рассчитать необходимое количество необходимого материала и закупить его, а работу предоставить специалистам;
3. Полностью самим сделать ремонт
Надо вооружиться здравым смыслом, математическими расчетами, советами и опытом специалистов.
Перед нами тоже встал вопрос: « Как наиболее дешево и качественно сделать ремонт »
И тогда учитель посоветовала провести опрос. Мы провели опрос среди 15 учителей нашей школы.
2.2 Анкетирование с целью изучения значимости выбранной темы проекта.
1. Если Вы собираетесь делать ремонт, то …
- воспользуетесь бригадой рабочих – 10%
- воспользуетесь помощью родственников и друзей – 35%
- выполните ремонт сами – 55%
| Профессионалы
| Знакомые и друзья | «своими руками»
|
| 10%
| 35% | 55%
|
![]()
2. Поясните свой вариант ответа
- хотите получить хороший результат – 40%
- хотите быть уверены в том, что вас не подведут – 10%
- хотите сэкономить на ремонте – 50%
| Хороший результат | Уверенность в качестве ремонта | Экономия |
| 40%
| 10% | 50%
|
![]()
3. Какую именно работу специалистов будите контролировать больше всего?
- приобретение строительных матералов– 10%
- качество работ – 50%
- смету расходов – 40%
| Приобретение материалов | Качество работ | Смета расходов |
| 10%
| 50% | 40%
|
![]()
Анкетирование с целью изучения значимости выбранной темы показало, что больше половины исследуемой аудитории учителей считает, что ремонт надо делать «своими руками». Потому что они хотят получить хороший результат и сэкономить на ремонте.
Конечно, более сложные работы, они считают, что должны выполнять специалисты. Поэтому им придется контролировать их работу. Контроль над качеством работ превосходит контроль над составлением сметы, т.к.многие еще не привыкли планировать и контролировать расходы.
Отсюда можно сделать вывод, что предпочтение отдано ремонту «своими руками».
А значит надо уже в школе учить составлять смету работ на уроках математики, а оформлению дизайна квартиры на уроках технологии. На уроках химии и биологии надо говорить об экологичности используемых материалов и о вреде их на здоровье человека.
2.3 Математические расчеты для ремонтных затрат
План-схема моей комнаты
(все измерения в м)
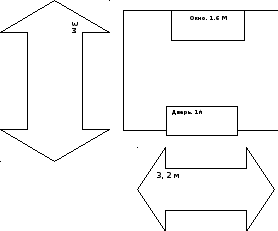
Таблица измерений комнаты для закупки строительных материалов
| СТЕНА 1 |
|
| Длина | 3,2 м |
| Высота | 2,5 м |
| СТЕНА 2 |
|
| Длина | 3м |
| Высота | 2,5м |
| ОКНО |
|
| Длина | 1,6м |
| Ширина | 1,5м |
| ДВЕРЬ |
|
| Ширина | 1 м |
На семейном совете было решено произвести покупку строительных материалов в магазине «Авега», что значительно сэкономит время.
Пол: замена старого линолеума на новый.
Расчеты по закупке (Приложение «Фото 5»).
Цена одного погонного метра:1700 тг.
Расчеты:
площадь пола = 3,2 ∙ 3 = 9,6 (м2)
надо купить: 9,6≈10кв.м.
цена единицы товара 1700тг
Плинтус для пола
Размер; 60х22х2500мм
Цена 340тг./штука
Расчеты:
Периметр пола = 13 м
13 : 2,5 = 5,2 шт.=6шт.
II. Потолок: приклеить потолочную плитку
| Размер: | 500х500х8шт (2 м2 ) |
Цена: 1 упаковки 2 м2 =400 тг
Расчеты (Приложение «Фото 6»):
площадь потолка = площади пола = 3,2*3 = 9,6м2 10м2
10 : 2 = 5 упаковок плитки необходимо закупить +1 упаковка на непредвиденные расходы
Потолочный плинтус
Расчеты:
Периметр потолка = (3,2+3) ∙ 2 = 12,4м 13м
13:2=6,5 необходимо купить 7шт
III. Стены: приклеить обои и часть стены выделить фотообоями
Мы произвели измерения оклеиваемой поверхности. Оконные и дверные проемы не включаются в расчеты (Приложение «Фото 6», «Фото 7» ).
Расчет:
- узнаем, сколько полотнищ требуемой длины содержится в одном рулоне 10: 2,5 =4 (высота потолка в комнате 2,5 м, из одного рулона, выбранных нами обоев получится 4 полотнища);
- после определения необходимого количества полотнищ узнаем, сколько метров стены можно оклеить четырьмя полотнищами. Для этого нужно умножить число полотнищ на ширину рулона, т. е. 4 х 0,52 =2,1 м. Значит, четырьмя полотнищами, полученными из одного рулона, можно оклеить стену на 2,1 метра по периметру помещения.
- узнаем необходимое количество рулонов. Для этого разделим периметр комнаты (без учета окон и дверей = ((3,2 + 3) ∙ 2) – (1,6 + 1) =19,8м 10м на 2,1 метров,
Итоговая таблица для покупки материалов
| Наименование товара | количество | стоимость в тенге |
| линолеум | 12 кв.м | 17000 |
| плинтус для пола | 6 штук | 2040 |
| плитка для потолка | 6 упаковок | 2400 |
| плинтус для пола | 7 штук | 1260 |
| Обои+клей | 5 рулонов | 8000тг |
|
|
| итого:30700 |
Мы выполнили расчет закупки необходимых материалов. Из итоговой таблицы видно, что основные затраты пошли на линолиум. Но линолиум – это качество и долговечность, естественность и теплота. Он может согреть даже самый экстремальный и минималистический интерьер.
Обзор литературных источников
При написании данного проекта были использованы научная и учебно-методическая литература.
Основными источниками, раскрывающими теоретические основы виличин и способов их измерения явились работы Клименченко Д. и Шабалина С.В данных источниках подробно рассмотрено понятие величины, место мотивации в структуре всех видов измерения и необходимости в потребности их знать.
Результаты и выводы
Рассчитана необходимая сумма для ремонта в соответствии с площадями поверхностей, которые нужно ремонтировать. Из выделенных родителями 50000тг в результате экономия составила около 15 тг.
Закончив свой проект, я могу сказать точно: математика- наука не только для ученых. (Приложение «фото 8», «фото 9», «фото 10»). Она нужна всем. В ходе этой работы я убедилась, насколько простой и увлекательной может быть математика. Работа над проектом показала мне, что без знания математики никакого ремонта не сделать.
Список использованных литературных источников
Клименченко Д. «Величины и их измерение». //Н. Ш., № 6, 1990
Шабалин С.А."Измерения для всех”. М.: Издательство стандартов, 1991
Ресурсы сети интернет (выбор строительных материалов для ремонта комнаты)
http://www.remont-delux.ru/raschet
http://www.shopvira.ru/Flizelinovye_oboi/
http://www.ext-decor.ru/
http://www.parquetline.ru/shponirovannyi-plintu
14

 Получите свидетельство
Получите свидетельство Вход
Вход












 Научный проект по математике "Математика в ремонте" (58.42 КB)
Научный проект по математике "Математика в ремонте" (58.42 КB)
 0
0 13756
13756 1718
1718 Нравится
0
Нравится
0


