 Модули в школе
Модули в школе
Кобаидзе Н. И. 2017 г.
В практикуме приведены подробные решения упражнений с модулями. Обратим внимание, что это только возможные схемы решения. Совсем необязательно, чтобы ученик решал именно так. Эти решения не являются безусловной рекомендацией для оформления. Учащимся известны 4 способа раскрытия модуля. В результате этого распределения получаются следующие способы раскрытия модуля и признаки их применения. Материалы взяты из школьных проектов (7-9 класс).
| Способ раскрытия модуля | Признаки применимости способа | Самоконтроль и коррекция |
| 1. По аналитическому определению модуля | В уравнении, неравенстве, системе есть только один модуль и выражение с переменной | 1.Решается две системы, включающие: первое неравенство – условие раскрытия модуля (неравенства), второе - результат раскрытия модуля при этом условии 2.Учитывается ОДЗ или выполняется проверка подстановкой |
| 2. Метод промежутков (алгоритм известен) | В уравнении, неравенстве, системе более двух модулей и выражение с переменной | Систем столько, сколько промежутков. В каждой системе: первое неравенство - условие промежутка (неравенство), второе - результат раскрытия всех модулей в соответствующем промежутке |
| 3.Возведение обеих частей в квадрат | В уравнении (неравенстве) один модуль: после возведения обеих частей в квадрат уравнение должно решаться | При возведении в квадрат обеих частей уравнения (неравенства) необходимо учитывать условие теоремы в том, что обе части должны быть неотрицательны. Для уравнения это условие может быть заменено проверкой (подстановкой) |
| 4.Определение модуля через расстояние (последний шаг решения) | Уравнение имеет вид: модуль выражения равен положительному числу | При решении неравенств получается либо двойное неравенство, либо объединение двух неравенств, записанных в одну строчку |
Примеры (из централизованных тестов)
П-1. Найти сумму корней уравнения: | x2-2x | = | 1-2x |. (8 – 9 класс)
Решение
(x2-2x)2-(1-2x)2=0; (x2-2x-1+2x)*(x2-2x+1-2x)=0; (x2-1)*(x2-4x+1)=0
x2-1=0 или x2-4x+1=0
x1,2=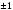 D=16-4=12; x3=
D=16-4=12; x3=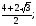 x3=2+
x3=2+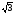 ; x4=
; x4=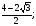 x4=2-
x4=2-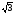 ; 1-1+2+
; 1-1+2+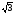 +2-
+2-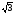 =4
=4 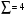 . Ответ: 4
. Ответ: 4
П-2. Найти среднее арифметическое всех корней уравнения: (7-9 класс)
| x-1 | + 2 * | x+3| = 5
Решение.
1) Найдем нули подмодульных выражений: x-1=0, x=1; x+3=0, x=-3
2) Числа -3 и 1 разбивают числовую прямую на три интервала.
Решаем уравнение на каждом интервале – таблица.
| Пример - 2 | x | -3 | x |
| x-1 | - | - | + |
| x+3 | - | + | + |
|
| 1-x-2*(x+3)=5 1-x-2x-6=5 -3x-10=0 x= -3 x= | 1-x+2*(x+3)=5 1-x+2x+6=5 x+7-5=0 x=-2 x=-2 корень | x-1+2*(x+3)=5 x-1+2x+6=5 3x+5=5 3x=0 x=0 нет корней |
Среднее арифметическое корней: 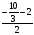 =-5
=-5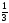 :2=
:2=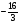 :2=
:2=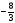 . Ответ:
. Ответ: 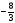
П-3. Найти произведение корней: | x2+x-3 | = x. (8 – 9 класс)
1) 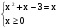 2)
2) ,
x2=3; x1,2=; x1=
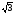 ; x2=
; x2= - не удов. x
; x2+x-3=0; x3=1; x4=-3 – не удов. x
Ответ: x1=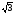 ; x2=1; x1*x2=
; x2=1; x1*x2=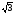 *1=
*1=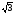
П-4. Найти произведение корней уравнения (7 - 9 класс)
| 2x-1 | + | x+1 | = 2x+1
Решение.
Найдем нули:
1) 2x-1=0; x=; x+1=0; x=-1
2) x+1 x+1
x
x x
-1
x
Решим на промежутках:
3) xx; -
;
1-2x+x+1=2x+1; -3x=-1
x= x1=
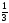 - корень уравнения;
- корень уравнения;
x, 2x-1+x+1=2x+1; x=1
); x2=1 – корень уравнения
4) Произведение корней равно: . Ответ:
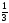 .
.
Упрощение выражений с модулем.
Применяем определение модуля или свойства модуля.
| a | =
a2= | a |2; | -a | =a, | a-b | = | b-a |
3) | ab | = | a | * | b | и | | =
Другие свойства модуля будут указаны в процессе решения задач.
Задача 1. Упростить выражение:
1) Нули подмодульных выражений: 0 и 1 делят числовую ось на промежутки:
(-;0), [0;1), (1;+
); дробь определена для a
1.
2) Упростить дробь на каждом из промежутков
| a | 0 | a1 |
| | | |
Ответ: при a (-
(-;0),
; при a
 [0;1), 1-a; при a
[0;1), 1-a; при a (1;+
(1;+), a-1.
З-2. Упростить выражение:
Решение
ОДЗ: выражение определено для всех значений x-1
1) Найдем нули подмодульных выражений: -1 и 1. Они разбивают числовую ось на промежутки: (-;-1), (-1;1), [1;+
)
2) Упростим выражение на каждом промежутке
a) x
б) -1x
в) x 1,
1,
Ответ: при x (-
(-;-1), 1; при x
 (-1;1),
(-1;1), при x
 [1;+
[1;+), 3.
З-3. Упростить выражение. .
Решение
Дробь определена на R, кроме 0.
x+x+1=(x+
)
+
при любых x. Дробь примет вид :
1) Найдем нули подмодульных выражений: -1; 0; 1. Они разбивают числовую ось на промежутки: (-;-1), [-1;0), (0;1), [1;+
).
2) Упростим выражение на каждом промежутке
а) при x ,
б)при -1 и 0x
в) при x,
Ответ: при xx; при x
1.
З-4. Найти сумму корней уравнения: (7 – 8 класс)
Решение. Дробь определена при x
|x-1|;
Найдем нули подмодульных выражений:
х -1=0, x=1 и x=0. Решим уравнение на каждом из промежутков:
| x | 0 | x |
|
Решений нет | 5=x x x x Следовательно, x=-2+ корень уравнения | 5-(4x-x 5-2x+x x x Следовательно, x=3 |
Сумма корней уравнения равна:
-2+. Ответ: 1+
Решение неравенств.
| x |
-a a x
-a [-a; a]
| x |a, a0
-a a x
-a
| x |
х=0
0 х
| x |x |
| x |a, a0 , нет решений
| x |
a0 x
| x |≥ а, а≥ 0, х – любое число,
7. | x | 0 , (-)
(0;
)
П-1. Найти число целых решений неравенства.
1
Решение
1; т.к.
1)
2 4 x
2) |x-3|3
;
0 6 x
3) Общее решение: [0;2][4;6]
0 2 4 6 Целые решения: 0,1,2,4,5,6
Ответ: 6
П-2. Найти наименьшее целое положительное решение неравенства.
Решение
1)
2) , не имеет решения
3) Общее решение: (-;-2)
(3;+
)
-2 3 4 x
Наименьшее положительное целое решение равно 4. Ответ: 4
П-3. Решить неравенство: (квадратичная функция) 9 класс
. Решение
1) 3x2-x-11
3x2-x-20
3x2-x-2=0; x1=1, x2=
3*(x-1)*(x)0
2) 3x2-x-1
3x2-xx2-x=0, x*(3x-1)=0
x=0; x=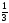
3x*(x-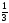 )
)
x*(3x-1)
0 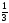 x
x
3) Общее решение: объединим эти решения
0
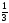 1 x
1 x
Ответ: (-;-
)
(0;
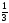 )
) (1;+
)
П-4. Решить уравнение
Решение
Пусть =y
 0, тогда
0, тогда
y2-5y+6=0, y1=3, y2=2
Значит:
1. , а)
,
б) , D
2.
а) ,
б) , D; 4; 1.
3

 Получите свидетельство
Получите свидетельство Вход
Вход


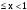
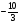
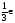 x
x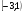

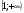









 Модули в школе - практикум (486.88 KB)
Модули в школе - практикум (486.88 KB)
 0
0 405
405 3
3 Нравится
0
Нравится
0









