Многогранники.
Работа
Рыженко Елены Владимировны , учителя математики и информатики
Мбоу г. Астрахани «сош № 64»

Содержание
- Введение
- Определение многогранника
- Правильные многогранники
(история и виды)
- Многогранники вокруг нас
- Заключение
- Источники информации

“ Правильных многогранников так мало, но это весьма скромный по численности отряд сумел пробраться в самые глубины различных наук ”.
Л. Кэрролл
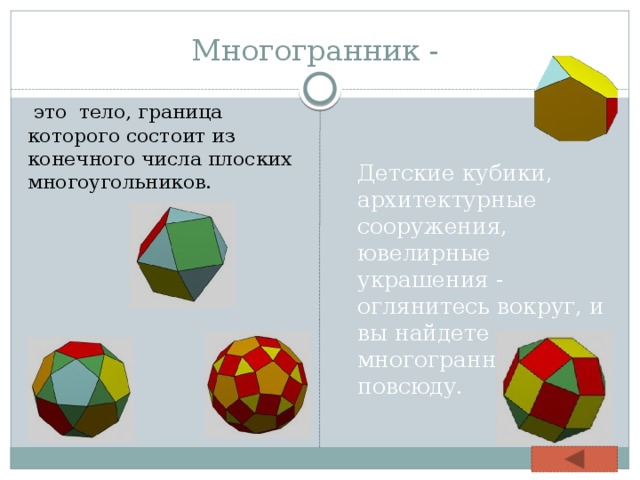
Многогранник -
это тело, граница которого состоит из конечного числа плоских многоугольников.
Детские кубики, архитектурные сооружения, ювелирные украшения - оглянитесь вокруг, и вы найдете многогранники повсюду.

МНОГОГРАННИК
часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников.
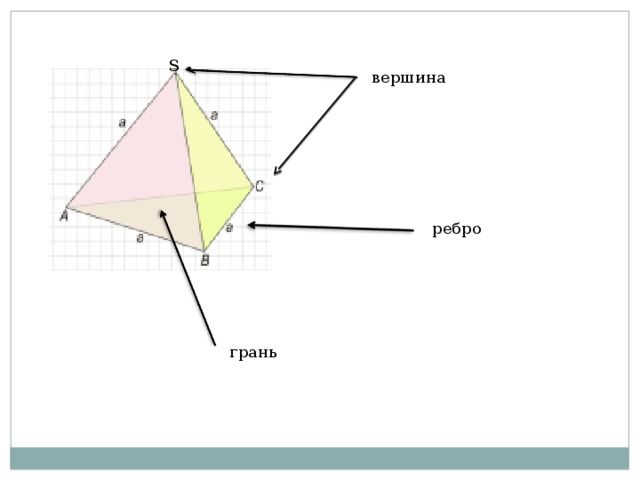
S
вершина
ребро
грань

Пространственным аналогом правильного многоугольника на плоскости является многогранник
МНОГОГРАННИК
РЕБРО
ГРАНЬ
ДВУГРАННЫЙ
УГОЛ
МНОГОУГОЛЬНИК
ВЕРШИНА
СТОРОНА
УГОЛ
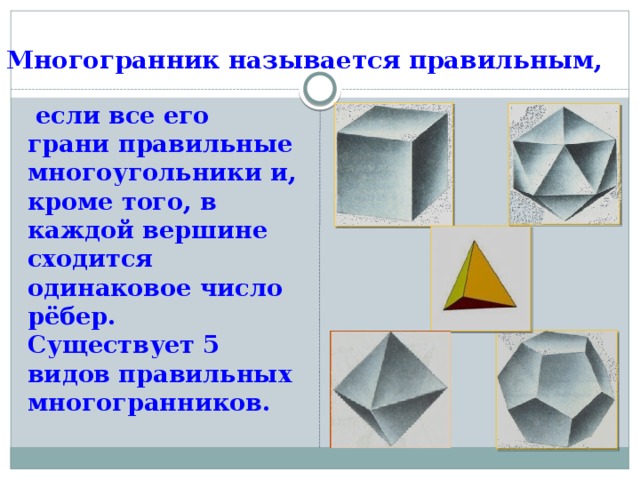
Многогранник называется правильным,
если все его грани правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число рёбер. Существует 5 видов правильных многогранников.
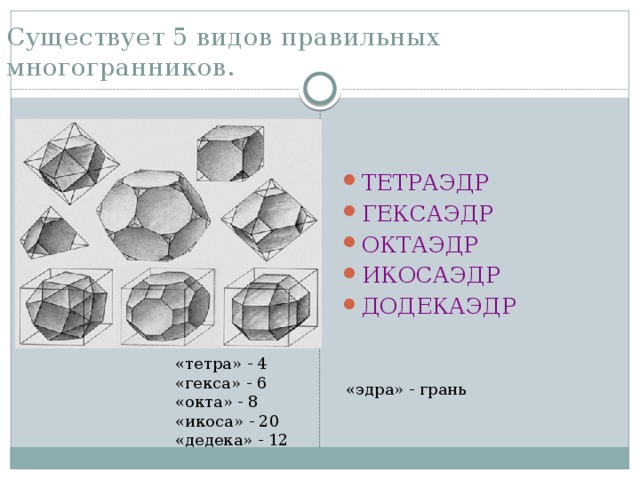
Существует 5 видов правильных многогранников.
- ТЕТРАЭДР
- ГЕКСАЭДР
- ОКТАЭДР
- ИКОСАЭДР
- ДОДЕКАЭДР
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«дедека» - 12
«эдра» - грань
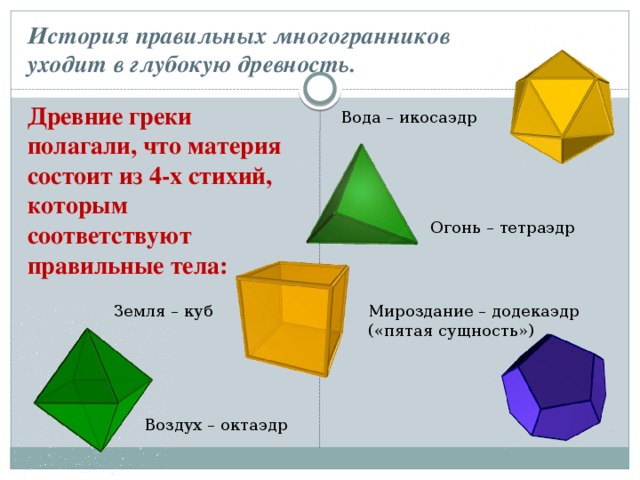
История правильных многогранников уходит в глубокую древность.
Древние греки полагали, что материя состоит из 4-х стихий, которым соответствуют правильные тела:
Вода – икосаэдр
Огонь – тетраэдр
Земля – куб
Мироздание – додекаэдр
(«пятая сущность»)
Воздух – октаэдр
Платон Евклид Архимед Кеплер
Все использовали в своих философских теориях
правильные многогранники.
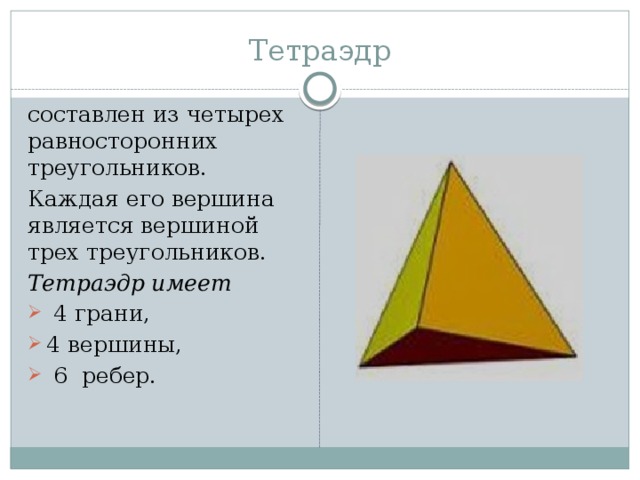
Тетраэдр
составлен из четырех равносторонних треугольников.
Каждая его вершина является вершиной трех треугольников.
Тетраэдр имеет
- 4 грани,
- 4 вершины,
- 6 ребер.
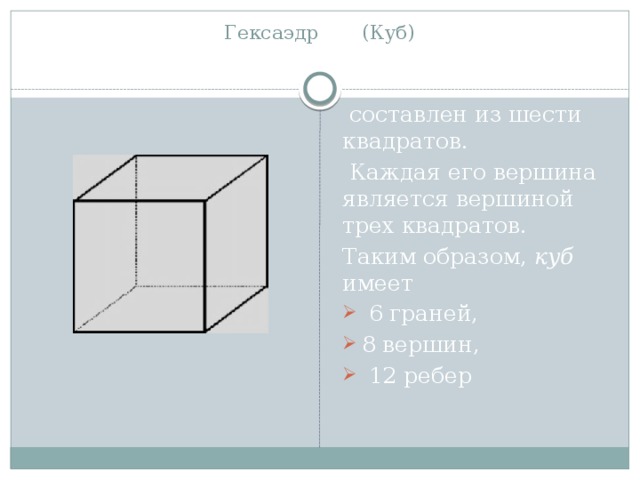
Гексаэдр (Куб)
составлен из шести квадратов.
Каждая его вершина является вершиной трех квадратов.
Таким образом, куб имеет
- 6 граней,
- 8 вершин,
- 12 ребер
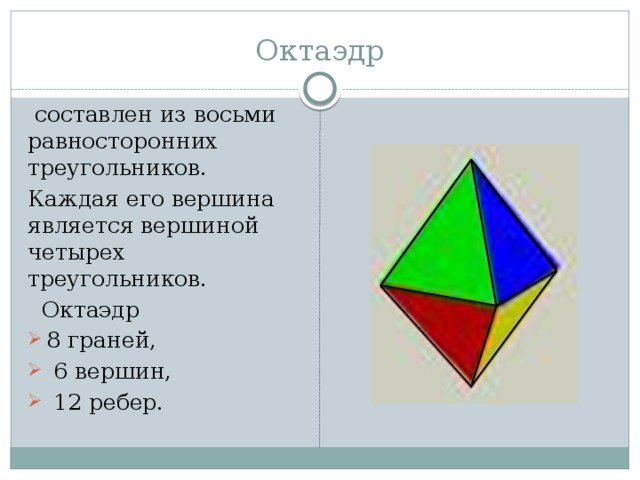
Октаэдр
составлен из восьми равносторонних треугольников.
Каждая его вершина является вершиной четырех треугольников.
Октаэдр
- 8 граней,
- 6 вершин,
- 12 ребер.

Икосаэдр
составлен из двадцати равносторонних треугольников.
Каждая его вершина является вершиной пяти треугольников.
Икосаэдр имеет
- 20 граней,
- 12 вершин,
- 30 ребер
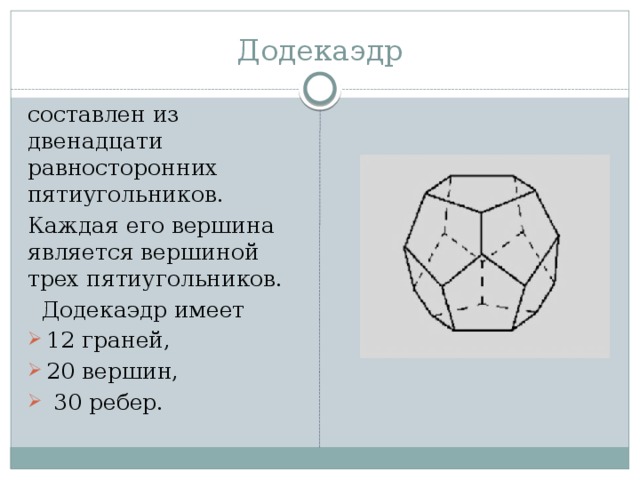
Додекаэдр
составлен из двенадцати равносторонних пятиугольников.
Каждая его вершина является вершиной трех пятиугольников.
Додекаэдр имеет
- 12 граней,
- 20 вершин,
- 30 ребер.

В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2.
Г+В=Р+ 2

Многогранники вокруг нас.
- В природе
- В архитектуре
- В искусстве

Чудо природы – кристаллы
Правильные многогранники - самые выгодные фигуры.
И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников:
- куб передает форму кристаллов поваренной соли NaCl
- монокристалл алюминиево-калиевых квасцов имеет форму октаэдра,
- кристалл сернистого колчедана FeS имеет форму додекаэдра,
- сернокислый натрий - тетраэдр,
- бор - икосаэдр.

Некоторые из выпуклых многогранников встречаются в природе в виде кристаллов
Халькопирит
Медный купорос
Авгит
Пирит
Топаз

Шеелит,5см, найден в Китае.
(блочное строение кристалла),

Друза кристаллов кварца (горный хрусталь),
9см, найден на Урале.

Гранаты: Андрадит и Гроссуляр ( найдены в бассейне реки Ахтаранда, Якутия)

Простейшее животное
Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр.
Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.
Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.
Это свойство помогает морскому организму преодолевать давление толщи воды.

В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН4, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

Пчёлы - удивительные создания.
Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов.
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»:
«Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».

Многогранники в архитектуре

Александрийский маяк

Многогранники в архитектуре Москвы
Собор непорочного зачатия
Девы Марии
на малой Грузинской
Исторический музей

Многогранники в архитектуре Москвы
Казанская церковь в Москве

Многогранники в архитектуре Москвы
Высотки. Котельники
ЦУМ

Многогранники в архитектуре Москвы
Телеграф

Многогранники в архитектуре Москвы
Новоарбатский замок
Малый Ржевский пер.

Многогранники в архитектуре Москвы
ул Пятницкая
«Поистине, живопись — наука и законная дочь природы, ибо она порождена природой»
Леонардо да Винчи
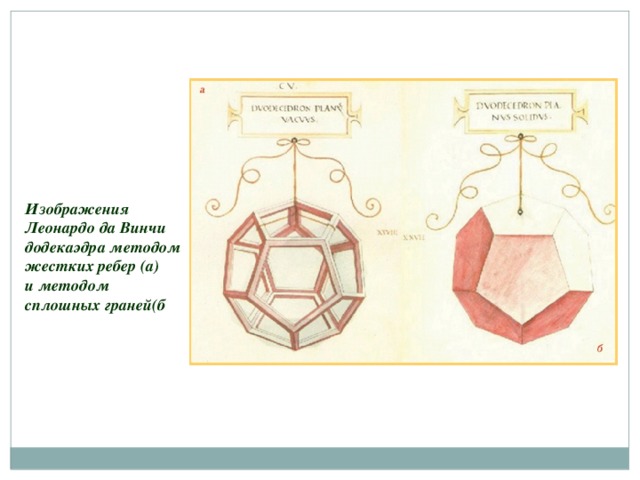
Изображения Леонардо да Винчи додекаэдра методом жестких ребер (а) и методом сплошных граней(б

Знаменитый художник, увлекавшийся геометрией,
Альбрехт Дюрер
(1471- 1528),
в известной гравюре «Меланхолия»
на переднем плане
изобразил додекаэдр.

Голландский художник Мориц Корнилис Эшер (1898-1972)создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей
"Четыре тела"
«Звезды»
"Порядок и хаос"

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра.
Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра

Многогранники в ювелирном деле
содержание
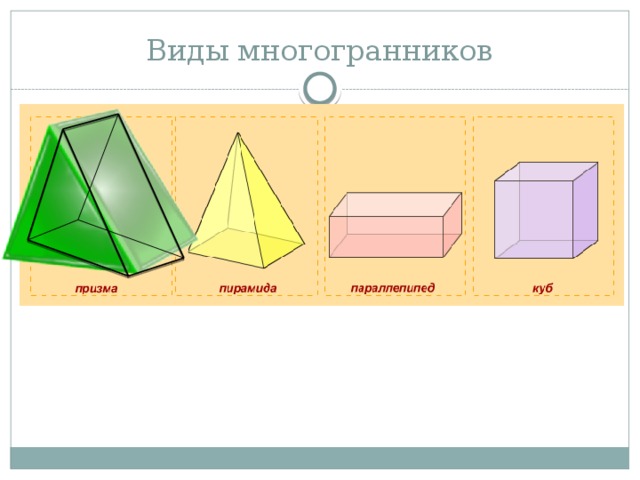
Виды многогранников

«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»
Бертран Рассел

Источники информации:
Литература
Интернет
- Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
http://www.nips.riss-telecom.ru/poly/
- Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.
Мир многогранников http://www.sch57.msk.ru:8101/collect/smogl.htm
- Ворошилов А.В. Математика и искусство. - М. просвещение, 1992. – 352
История математики http://mschool.kubsu.ru/
- Рыбников К.А. История математики: Учебник. - М.: Изд-во МГУ, 1994. - 495 с
Библиотека электронных учебных пособий http://www.ega-math.narod.ru/
Статьи по математике http://dondublon.chat.ru/math.htm
Популярная математика http://www.uic.ssu.samara.ru/~nauka/index.htm
«В мире науки» http://www.mccme.ru/
Московский центр непрерывного математического образования
http://mathc.chat.ru/
Математический калейдоскоп
file:///C:/Users/school/Desktop/ МНОГОГРАНИКИ
Урок-конференция "Многогранники вокруг нас«
- www. samara.edu.ru.
- www. rspu.ru
- www.edu.hmao.ru
- www. tspu.ru
- www.nvp.region.ru


 Получите свидетельство
Получите свидетельство Вход
Вход






















































 Многогранники (7.7 MB)
Многогранники (7.7 MB)
 0
0 1120
1120 15
15 Нравится
0
Нравится
0







