
МАТЕРИАЛЫ ДЛЯ УСТНОЙ РАБОТЫ НА УРОКАХ АЛГЕБРЫ В 7 КЛАССЕ
- Устные тесты,
- устные упражнения;
- математические диктанты,
- развивающие таблицы.
Учитель Козина Н.А.

x 3
ax 2
+
2ab
-

МНОГОЧЛЕНЫ
- Раскройте скобки:
- а) (5 x + 2) · 7 =
- б) 8 · (x – 3) =
- в) 12 · (10 – 3 b) =
- 3 5 x + 14;
- 8x – 24;
- 12 0 – 3 6b.

МНОГОЧЛЕНЫ

МНОГОЧЛЕНЫ
МНОГОЧЛЕНЫ
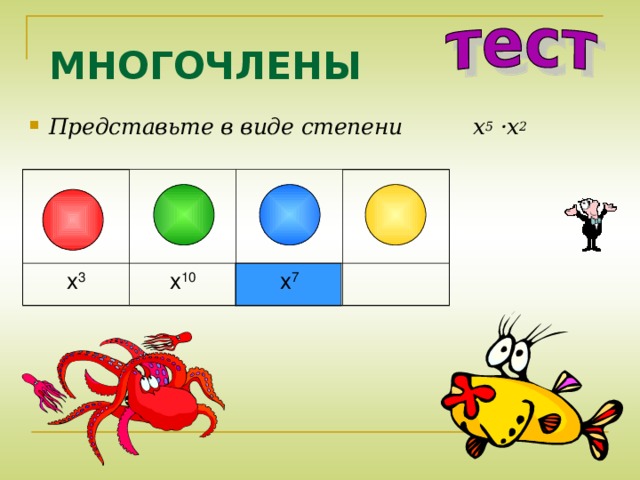
- Представьте в виде степени x 5 ·x 2
x 3
x 10
x 7
МНОГОЧЛЕНЫ
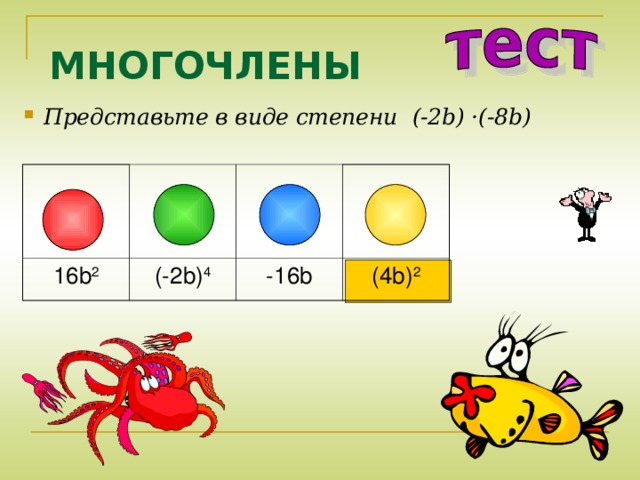
- Представьте в виде степени (-2 b) ·(-8b)
16b 2
(-2b) 4
-16b
(4b) 2
МНОГОЧЛЕНЫ
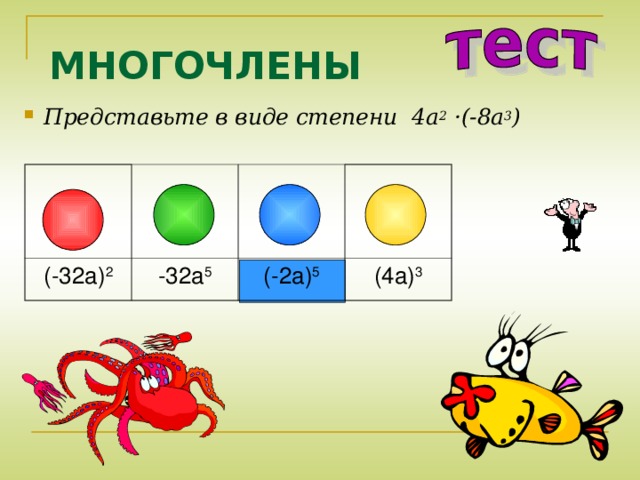
- Представьте в виде степени 4a 2 ·(-8a 3 )
(-32a) 2
-32a 5
(-2a) 5
(4a) 3
МНОГОЧЛЕНЫ
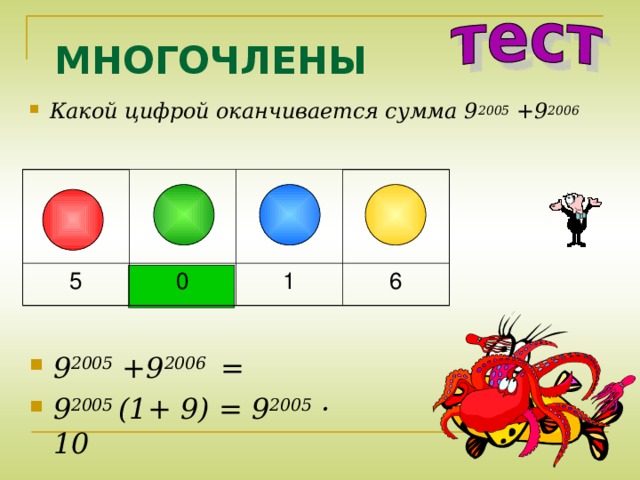
- Какой цифрой оканчивается сумма 9 2005 +9 2006
5
0
1
6
- 9 2005 +9 2006 =
- 9 2005 (1+ 9) = 9 2005 · 10
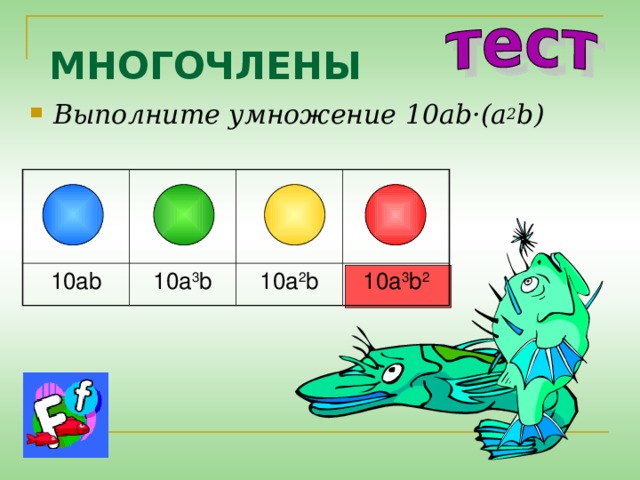
МНОГОЧЛЕНЫ
- Выполните умножение 10ab·(a 2 b)
10ab
1 0 a 3 b
1 0a 2 b
10a 3 b 2
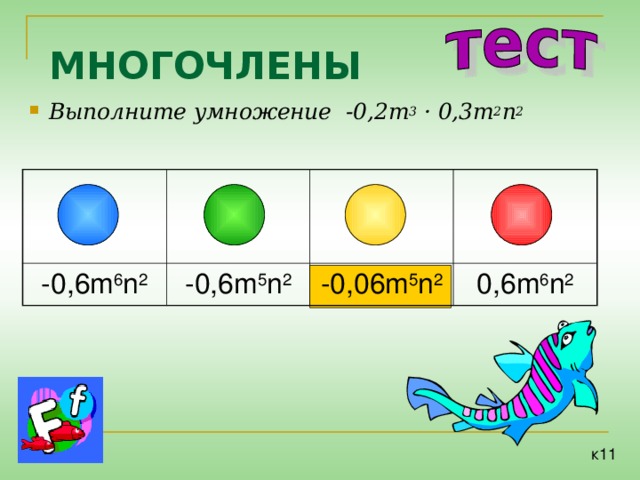
МНОГОЧЛЕНЫ
- Выполните умножение -0 ,2m 3 · 0,3m 2 n 2
-0,6m 6 n 2
-0,6m 5 n 2
-0,06m 5 n 2
0,6m 6 n 2
к11

МНОГОЧЛЕНЫ

МНОГОЧЛЕНЫ
- При каких значениях x значение выражения 2x + 1 равно -1 :
- При каких значениях x значение выражения 2x + 1 равно 0:
- 2x + 1 = -1 ;
- 2 x = -2;
- x = -1.
- 2x + 1 = 0;
- 2 x = -1;
- x = -0,5.
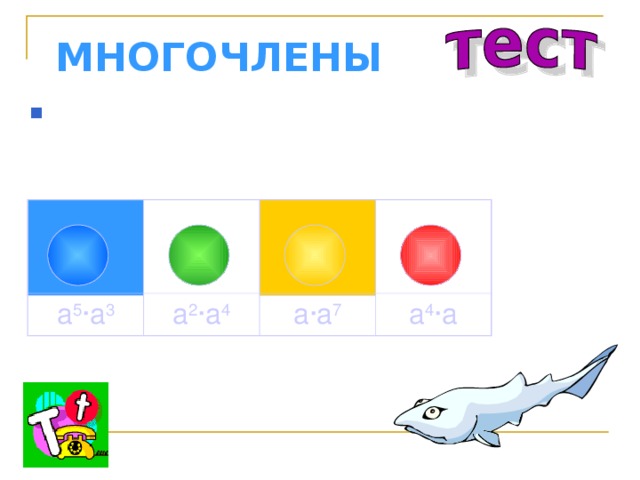
МНОГОЧЛЕНЫ
- Представьте в виде произведения двух одночленов a 8
a 5 ·a 3
a 2 ·a 4
a ·a 7
a 4 ·a
МНОГОЧЛЕНЫ
- Представьте в виде произведения двух одночленов 2y 7
2y 5 ·y 3
2y 2 ·y 5
y ·y 7
y 4 ·2y 3
МНОГОЧЛЕНЫ
- Представьте в виде произведения двух одночленов 6b 6
2b 5 ·b
2b 2 ·3b 4
6b 6 ·1
3b 2 ·2b 3

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Запишите выражения:
- Произведение разности x и y и их суммы;
- Запишите выражения:
- Сумма квадратов a и b;

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Запишите выражения:
- Квадрат разности a и b;
- Запишите выражения:
- Удвоенное произведение x и y;

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Запишите выражения:
- Разность кубов a и b;
- Запишите выражения:
- Квадрат суммы m и n;
- Запишите выражения:
- Разность квадратов x и y;

ОТВЕТЫ
- (x – y)(x + y);
- a 2 + b 2 ;
- (a – b) 2 ;
- 2xy;
- a 3 – b 3 ;
- (m + n) 2 ;
- X 2 – y 2 .

МНОГОЧЛЕНЫ
- 5,8 2 + 5,8 · 4,2 =
- 5,8 (5,8 + 4,2) =
- 5,8 · 10 = 58.
- Вычислите:
- 99 + 99 2 =
- 99(1 + 99) =
- 99 · 100=
- 9900.

МНОГОЧЛЕНЫ

МНОГОЧЛЕНЫ
- (x-5)(x+2)=0
- x=5 или x =-2

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Вынести за скобки общий множитель:
- 6m – 9n;
- -10-10c;
- 3x+6x 2 ;
- -xy-y 2 ;
- -4x 2 y 2 +16x 3 y.
- 3(2m – 3)n;
- -10(1+c);
- 3x(1+2x);
- -y(x+y);
- -4x 2 y(y-4x).

МНОГОЧЛЕНЫ
- Какие одночлены следует подставить вместо (*), чтобы получилось тождество: x 3 · (*) = x 12
x 4
x 9
-x 15
x 6

МНОГОЧЛЕНЫ
- Какие одночлены следует подставить вместо (*), чтобы получилось тождество: -a 6 =a 4 · (*)
a 2
a 2
-a 2
-a 3

МНОГОЧЛЕНЫ
- Какие одночлены следует подставить вместо (*), чтобы получилось тождество: (*) · y 7 = y 8
y
-y
y 0,7
y -9

- Упростите выражение
- (5x 2 – 2x +3) – (3x 2 – 7)
- Раскройте скобки
- 7 a 3 (a – 2a 2 ).
- Вынесите за скобки общий множитель
- 8 ab – 8ac

- Вынесите за скобки общий множитель
- 16xy 2 + 12x 2 y
- Решите уравнение
- x 2 + 5x = 0.

- 2x 2 – 2x + 10;
- 7a 4 – 14a 5 ;
- 8a (b – c);
- 4xy (4y + 3x);
- 0;-5.
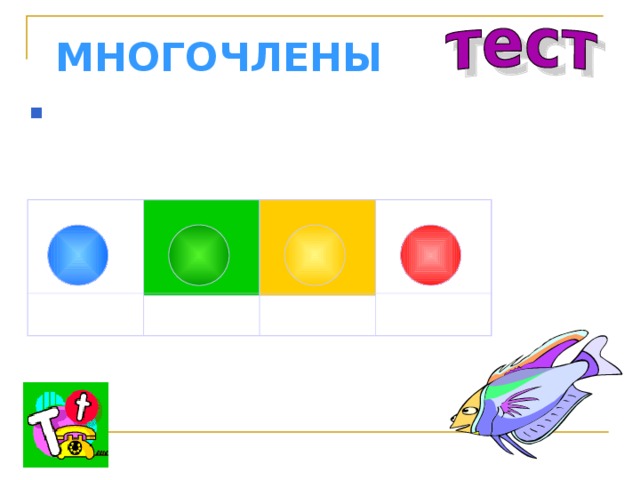
МНОГОЧЛЕНЫ
- Представьте одночлен 12 x 3 y 4 в виде произведения двух одночленов, один из которых равен 2 x 3 :
3x 3 y 4
6y 4
6x 3 y 4
4y 4
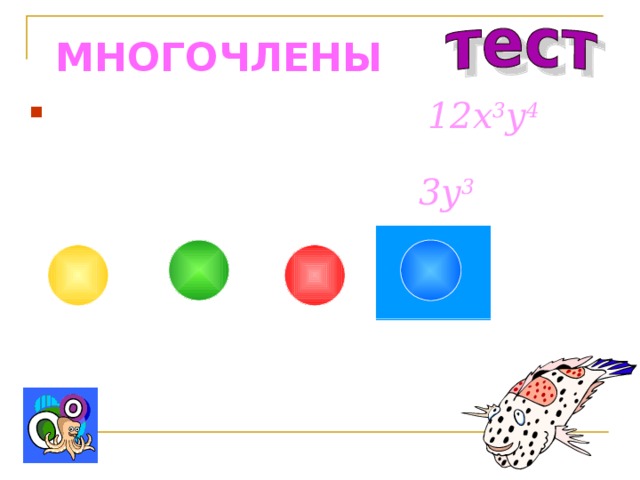
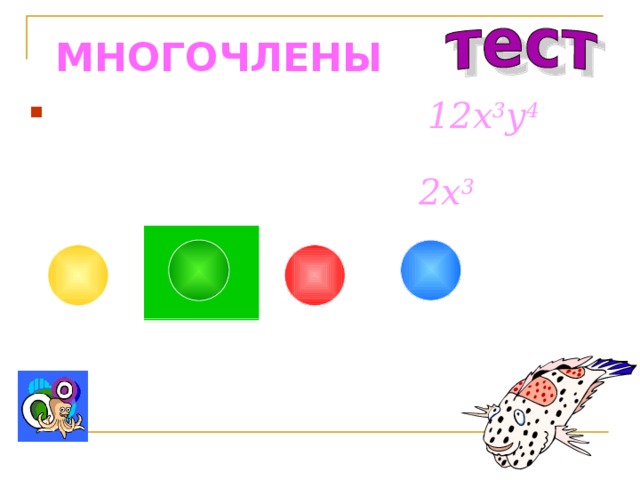
МНОГОЧЛЕНЫ
- Представьте одночлен 12 x 3 y 4 в виде произведения двух одночленов, один из которых равен 3y 3 :
4x 3 y 4
6x 3 y
4x 3 y 4
4x 3 y
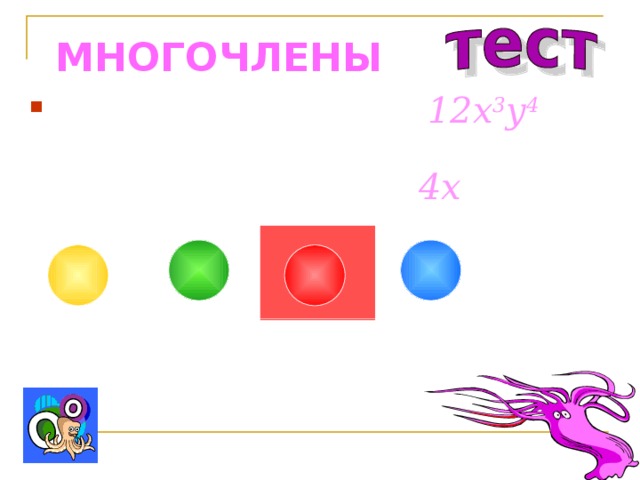
МНОГОЧЛЕНЫ
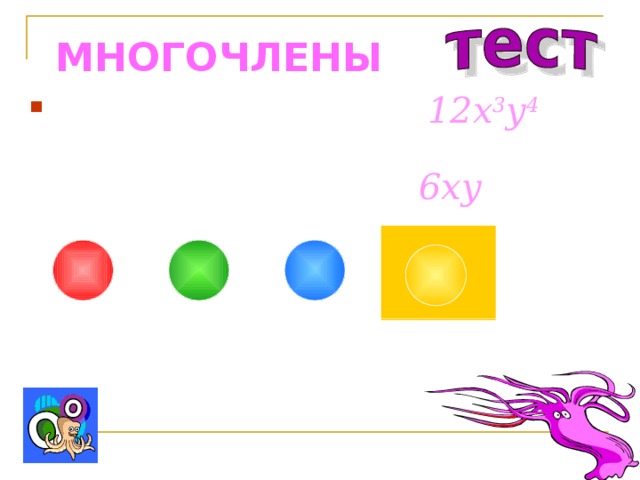
- Представьте одночлен 12 x 3 y 4 в виде произведения двух одночленов, один из которых равен 4x :
3x 3 y 4
6x 3 y 4
3x 2 y 4
4x 3 y 4
МНОГОЧЛЕНЫ
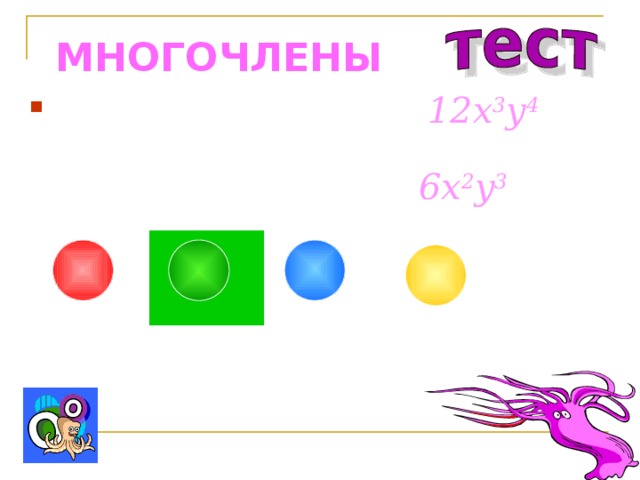
- Представьте одночлен 12 x 3 y 4 в виде произведения двух одночленов, один из которых равен 6xy :
2x 3 y 3
2x 2 y 4
3x 2 y 3
2x 2 y 3
МНОГОЧЛЕНЫ
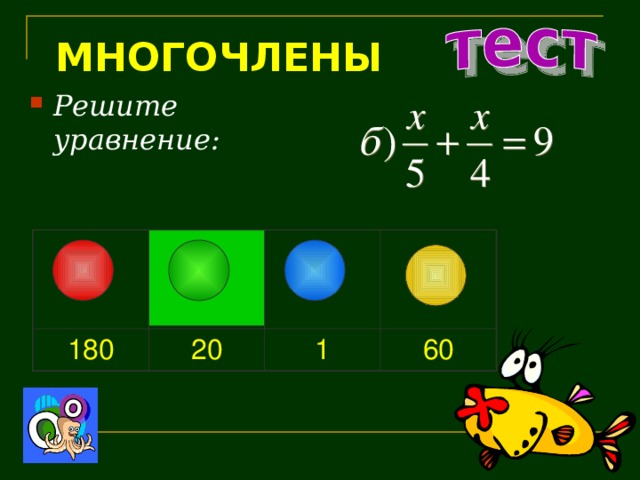
- Представьте одночлен 12 x 3 y 4 в виде произведения двух одночленов, один из которых равен 6x 2 y 3 :
2x 2 y 3
2xy
3xy
2x 2 y 4
МНОГОЧЛЕНЫ
180
2 0
1
60
МНОГОЧЛЕНЫ
1,5
2 4
8
2

МНОГОЧЛЕНЫ
-10 x+1
-x+2
-10x-1
-5x+4
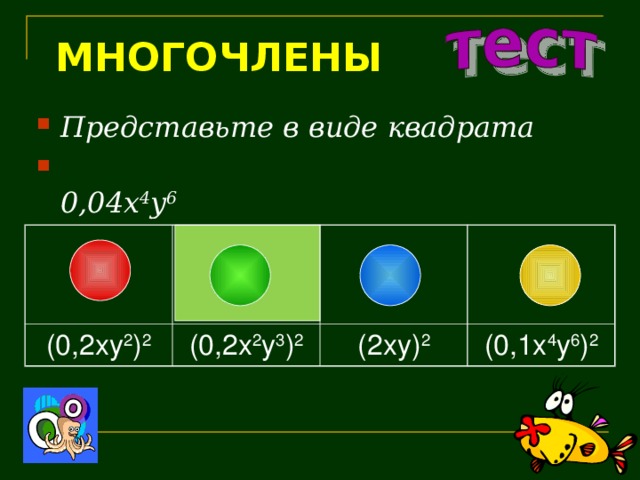
МНОГОЧЛЕНЫ
- Представьте в виде квадрата
- 0,04 x 4 y 6
(0,2xy 2 ) 2
(0,2x 2 y 3 ) 2
(2xy) 2
(0,1x 4 y 6 ) 2

МНОГОЧЛЕНЫ
- 2x + 6 =
- 8x – 12y =
- 6ab + a =
- x 2 – x =
- a 3 – 2a 4 + 3a 5 =
- x 2 + xy =
- 2(x + 3);
- 4(2x – 3y);
- a(6b + 1);
- x(x – 1);
- a 3 (1 – 2a + 3a 2 );
- x(x + y).

МНОГОЧЛЕНЫ
- Найдите значение выражения x 3 + 2x 2 при x = -2 :
- Если x = -2 , то x 3 + 2x 2 = (-2) 3 + 2(-2) 2 =
- -8 + 8 = 0
- Какие из следующих пар ( a;b) удовлетворяют равенству ab = 0 :
- (5 ;2),
- (0;17),
- (13;0),
- (0;0).

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Упростите выражение
- (8 a 2 – 5a + 1) – (2a – 3)
- Раскройте скобки
- 3x 3 (2x 2 + x).
- Вынесите за скобки общий множитель
- 10xy + 5y

МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- Вынесите за скобки общий множитель
- 18mn 3 – 9m 2 n
- Решите уравнение
- 3 x 2 – x = 0.

ОТВЕТЫ
- 8 a 2 – 7a + 4
- 6x 5 + 3x 4
- 5y (2x + 1)
- 9mn (2n 2 – m)
- 0; 1/3.

МНОГОЧЛЕНЫ
- Решите уравнение:
- x 2 – 2x = 0;
- x(x – 2) = 0;
- x = 0 или x – 2 = 0;
- x = 2;
- Ответ: 0;2.

МНОГОЧЛЕНЫ
- Решите уравнение:
- x 2 + 0,1 x= 0;
- x(x + 0,1) = 0;
- x = 0 или x + 0,1 = 0;
- x = -0,1;
- Ответ: 0; -0,1 .

МНОГОЧЛЕНЫ
- Решите уравнение:
- x 3 + x= 0;
- x(x 2 + 1) = 0;
- x = 0 или x 2 + 1 = 0;
- x 2 = -1;
- нет корней
- Ответ: 0.
МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Произведение разности x и y и их суммы.
xy–(x + y)
xy-x+y
(x-y)(x+y)
x+y-xy
МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Сумма квадратов чисел a и b .
(a + b) 2
a 2 + b 2
(a – b) 2
a 2 – b 2

МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Квадрат разности чисел m и n .
m 2 – n 2
(m +n) 2
(m – n) 2
m 2 + n 2

МНОГОЧЛЕНЫ
- Представьте в виде квадрата выражение 4 x 2 y 4
4(xy 2 ) 2
(4xy 2 ) 2
16x 2 y 8
(2xy 2 ) 2
МНОГОЧЛЕНЫ
- Представьте в виде куба выражение 0,001a 6 b 3
(0,1a 6 b 3 ) 3
(0,1a 2 b) 3
0,001(ab) 3
(0,1ab) 3

МНОГОЧЛЕНЫ
- Решите уравнение:
- x 2 - 9x= 0;
- x (x - 9) = 0;
- x = 0 или x - 9 = 0;
- x = 9;
- Ответ: 0; 9 .

МНОГОЧЛЕНЫ
- (a - b) (a + b);
- a 2 + b 2 ;
- (a + b) 2 ;
- m 2 – n 2 ;
- (b – c) 3 ;
- b 3 + c 3 .
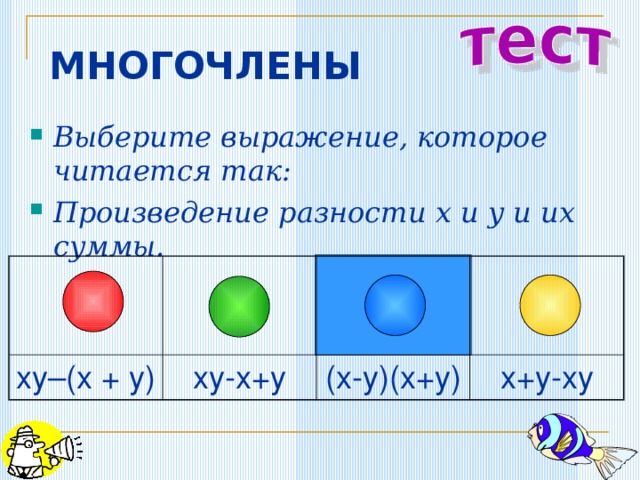
МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Произведение разности x и y и их суммы.
xy–(x + y)
xy-x+y
(x-y)(x+y)
x+y-xy
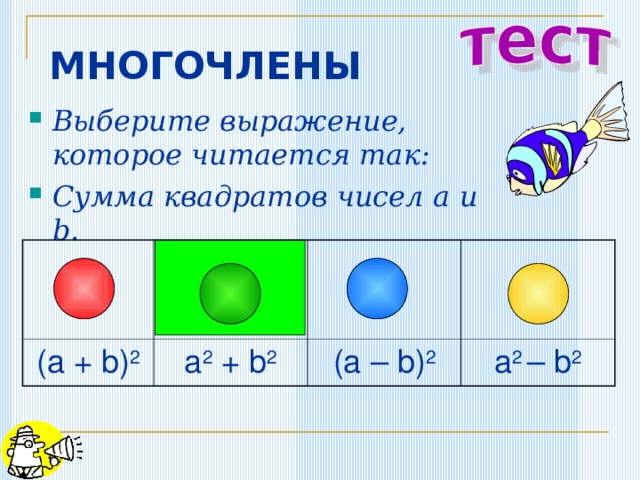
МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Сумма квадратов чисел a и b .
(a + b) 2
a 2 + b 2
(a – b) 2
a 2 – b 2
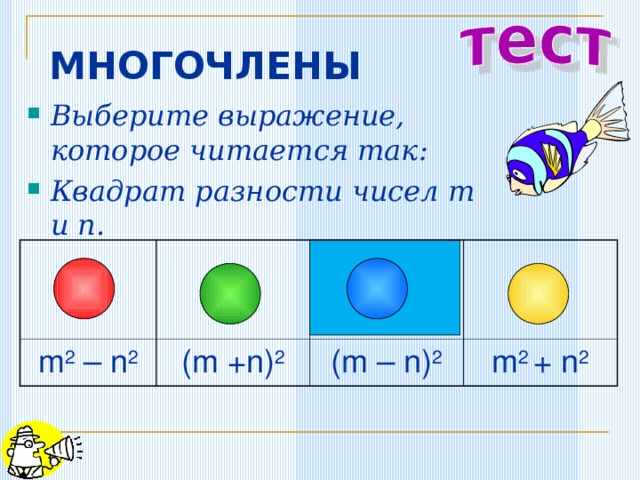
МНОГОЧЛЕНЫ
- Выберите выражение, которое читается так:
- Квадрат разности чисел m и n .
m 2 – n 2
(m +n) 2
(m – n) 2
m 2 + n 2
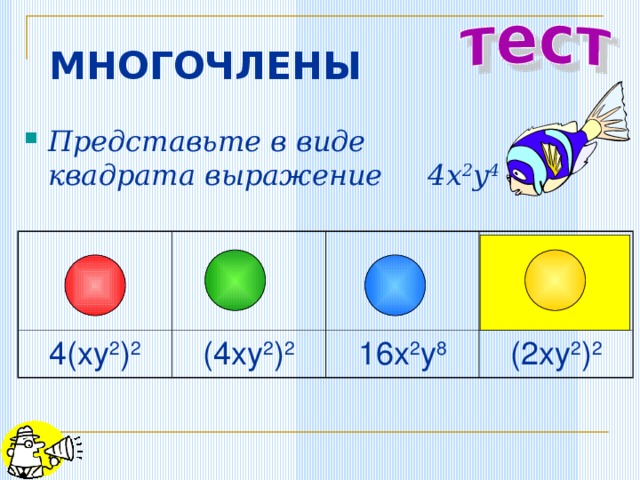
МНОГОЧЛЕНЫ
- Представьте в виде квадрата выражение 4 x 2 y 4
4(xy 2 ) 2
(4xy 2 ) 2
16x 2 y 8
(2xy 2 ) 2
МНОГОЧЛЕНЫ
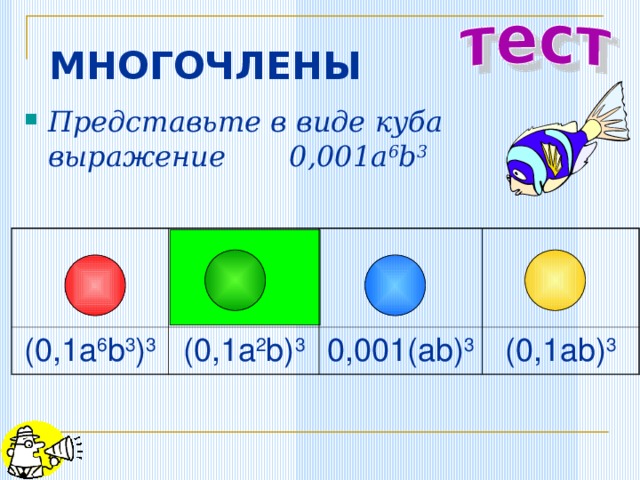
- Представьте в виде куба выражение 0,001a 6 b 3
(0,1a 6 b 3 ) 3
(0,1a 2 b) 3
0,001(ab) 3
(0,1ab) 3

МНОГОЧЛЕНЫ
- Решите уравнение:
- x (x + 2) – 7(x + 2) = 0;
- (x + 2)(x – 7) = 0;
- x + 2= 0 или x - 7 = 0;
- x = -2; x = 7;
- Ответ: -2 ; 7 .

МНОГОЧЛЕНЫ
- Докажите, что при любом натуральном n выражение n 2 + n кратно 2.
- n 2 + n = n (n + 1)
- n и n + 1 последовательные натуральные числа, значит, одно из них четное, т.е. кратно 2.
- Таким образом, произведение n (n+1) кратно 2.

МНОГОЧЛЕНЫ
- Разложите на множители:
- 2 (x – y) + x (x – y) =
- 2 (a – b) – c (a – b) =
- (a + 1) – a (a + 1) =
- (x – y)(2 + x);
- (a – b)(2 – c);
- (a + 1)(1 – a).

МНОГОЧЛЕНЫ
- Разложите на множители:
- 7 (a – b) + x (a – b) =
- 2 (x – y) – c (y – x) =
- a (b - c) 2 – (c - b) 2 =
- (a – b)(7 + x);
- (x – y)(2 + c);
- (b - c) 2 (a – 1).
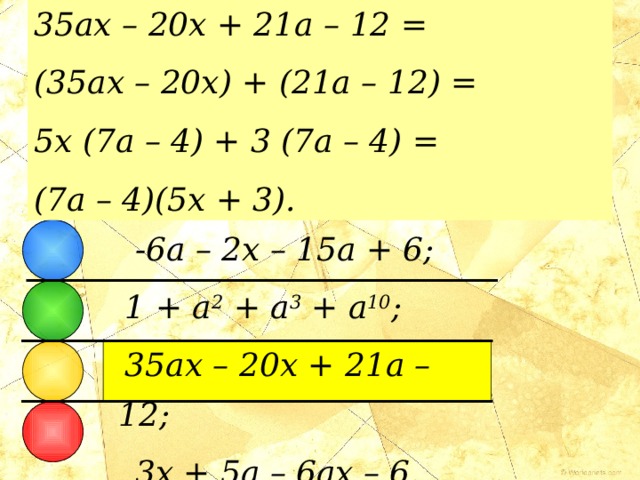
35ax – 20x + 21a – 12 =
(35ax – 20x) + (21a – 12) =
5x (7a – 4) + 3 (7a – 4) =
(7a – 4)(5x + 3).
МНОГОЧЛЕНЫ
- Из следующих многочленов только один можно разложить на множители. Какой?
- 6a – 2x – 15a + 6;
1 + a 2 + a 3 + a 10 ;
35ax – 20x + 21a – 12;
3x + 5a – 6ax – 6.
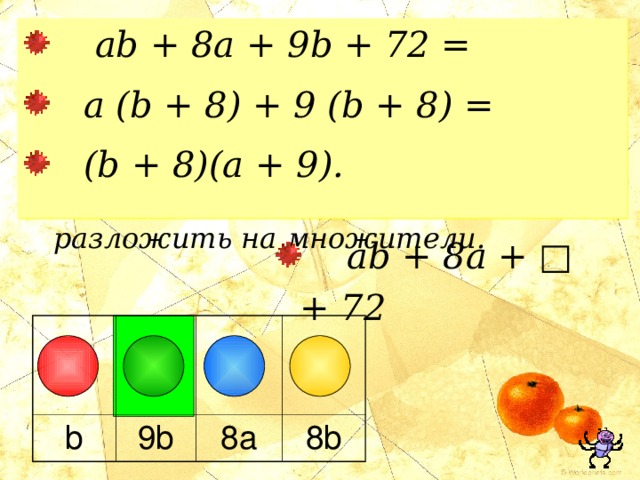
- ab + 8a + 9 b + 72 =
- a (b + 8) + 9 (b + 8) =
- (b + 8)(a + 9).
МНОГОЧЛЕНЫ
- Вместо квадратика запишите такое выражение, чтобы полученный многочлен можно было разложить на множители.
b
9b
8a
8b
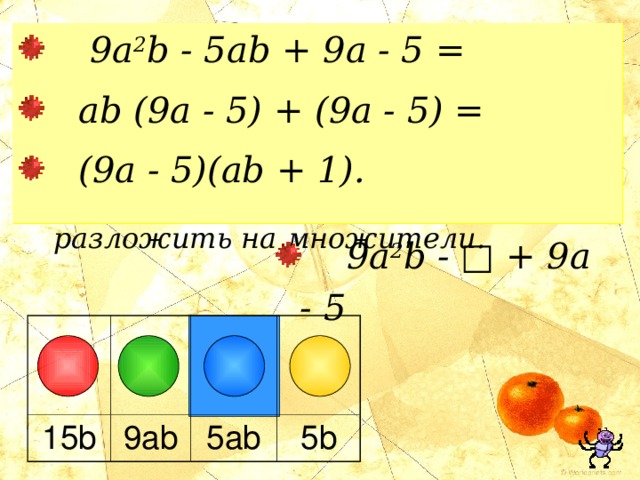
- 9a 2 b - 5ab + 9 a - 5 =
- ab (9a - 5) + (9a - 5) =
- (9a - 5)(ab + 1).
МНОГОЧЛЕНЫ
- Вместо квадратика запишите такое выражение, чтобы полученный многочлен можно было разложить на множители.
15b
9ab
5ab
5b

МНОГОЧЛЕНЫ
- 2xy - 4 + 3xy 2 – 6y =
- 2 (xy - 2) + 3y(xy - 2) =
- (xy - 2)(2 + 3y).
- Вместо квадратика запишите такое выражение, чтобы полученный многочлен можно было разложить на множители.
6y
12x
3y
xy

№ 1 Выполните действия : 4x 2 – 3x ( 2x – 1 );
№ 2 Выполните действия : (a + 4 )( a + 8 );
№ 3 Вынесите за скобки общий множитель
60x 2 – 5x 4 ;
№ 4 Вынесите за скобки общий множитель
7 a 2 b + ab;
№ 5 Разложите на множители : am + bm + 7a + 7b.







№ 1 Выполните действия : 4x 2 – 3x ( 2x – 1 );
№ 2 Выполните действия : (a + 4 )( a + 8 );
№ 3 Вынесите за скобки общий множитель
60x 2 – 5x 4 ;
№ 4 Вынесите за скобки общий множитель
7 a 2 b + ab;
№ 5 Разложите на множители : am + bm + 7a + 7b.


4 x 2 – 3x(2x – 1) = 4x 2 – 6x 2 + 3x = -2x 2 + 3x;
(a + 4)(a + 8) = a 2 + 8a + 4a + 32 = a 2 + 12a + 32;
60x 2 – 5x 4 = 5x 2 ( 12 – x 2 );
7a 2 b + ab = ab(7a + 1 );
am + bm + 7a + 7b = m ( a + b ) + 7 ( a + b ) = ( a + b ) (m +7 ).
Запишите выражения :
Разность квадратов x и y;
Квадрат суммы m и n;
Удвоенное произведение a и b .
Выполните действия : 5a 2 ( 3a + 4 );
Выполните действия : (x + 2)(x + 7);
Вынесите за скобки общий множитель
4a(a + 1) – 7 (a + 1);
Разложите на множители способом группировки
2b + ab 2 – a 2 b – 2a.

Запишите выражения :
Разность квадратов x и y;
Квадрат суммы m и n;
Удвоенное произведение a и b .
Выполните действия : 5a 2 ( 3a + 4 );
Выполните действия : (x + 2)(x + 7);
Вынесите за скобки общий множитель
4a(a + 1) – 7 (a + 1);
Разложите на множители способом группировки
2b + ab 2 – a 2 b – 2a.

x 2 – y 2 ; (m + n) 2 ; 2ab.
5a 2 (3a + 4) = 15a 3 + 20a 2 ;
(x + 2)(x + 7) = x 2 + 9x + 14;
4a (a + 1) -7 (a + 1) = (a + 1)(4a -7);
2b + ab 2 – a 2 b - 2a =
b (2 + ab) – a (ab + 2) =
(ab + 2)(b - a).
Запишите выражения :
Квадрат разности a и b;
Разность квадратов x и y;
Утроенное произведение m и n;
Разложите на множители : a) 3(x – 1) + x 2 (x – 1);
в) (x – 2) 2 + 4(x – 2);
г) 8x + ay + 8y + ax;
д) ax + ay – x - y
Запишите выражения :
Квадрат разности a и b;
Разность квадратов x и y;
Утроенное произведение m и n;
Разложите на множители : a) 3(x – 1) + x 2 (x – 1);
в) (x – 2) 2 + 4(x – 2);
г) 8x + ay + 8y + ax;
д) ax + ay – x - y

(a – b) 2 ; x 2 – y 2 ; 3mn.
3(x – 1) + x 2 (x – 1) = (x – 1)(3 + x 2 )
(x – 2) 2 + 4(x – 2) = (x – 2)(x – 2 +4) = (x – 2)(x + 2)
8x + ay + 8y + ax = 8 (x + y) + a (x+y) = (x + y)(8 + a)
ax + ay – x – y = a (x+y) – (x + y) = (x + y)(a – 1).
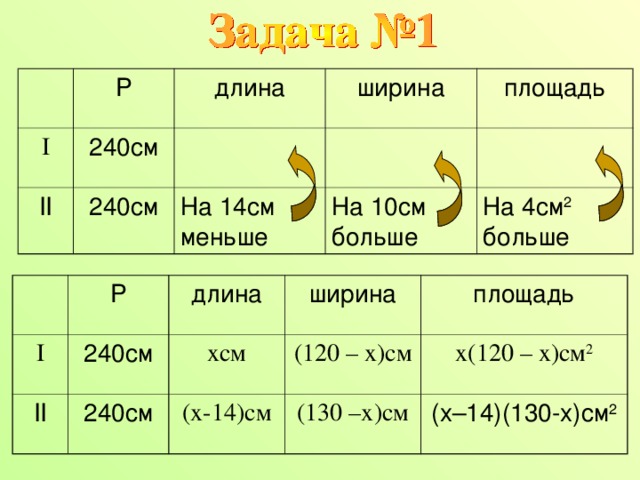
Периметр прямоугольного треугольника равен 240см. Если длину прямоугольника уменьшить на 14см, а ширину увеличить на 10см, то площадь прямоугольника увеличится на 4см 2 . Найдите длины сторон прямоугольника.
I
P
II
длина
240см
ширина
240см
площадь
На 14см меньше
На 10см больше
На 4см 2 больше
P
I
240см
II
длина
240см
ширина
На 14см меньше
площадь
На 10см больше
На 4см 2 больше
I
P
II
длина
240см
ширина
x см
240см
(120 – x)c м
( x-14) см
площадь
x(120 – x) см 2
(130 – x )см
(x–14)(130 - x) см 2
P
I
длина
II
240см
x см
240см
ширина
(120 – x)c м
площадь
( x-14) см
x(120 – x) см 2
(130 – x )см
(x–14)(130 - x) см 2
(x-14)(130 – x) – x(120 – x) = 4;
130x – x 2 - 1820 + 14x – 120x + x 2 = 4;
24x = 1824;
x = 76;
1) 120 – 76 = 44(c м );
длина – 44см ; ширина – 76см.

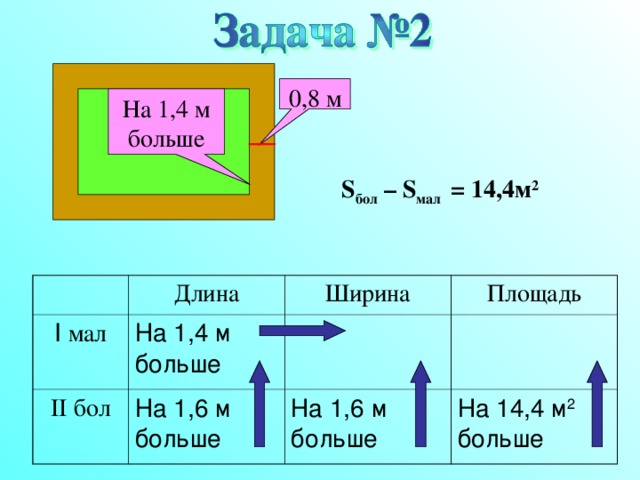
Клумба прямоугольной формы окружена дорожкой ширина которой 0,8м. Площадь дорожки 14,4м 2 . Найдите стороны клумбы, если одна из них на 1,4 больше другой.
0,8 м
На 1,4 м больше
S бол – S мал = 14,4м 2
0,8 м
На 1,4 м больше
S бол – S мал = 14,4м 2
Длина
I мал
Ширина
II бол
На 1,4 м больше
Площадь
На 1,6 м больше
На 1,6 м больше
На 14,4 м 2 больше
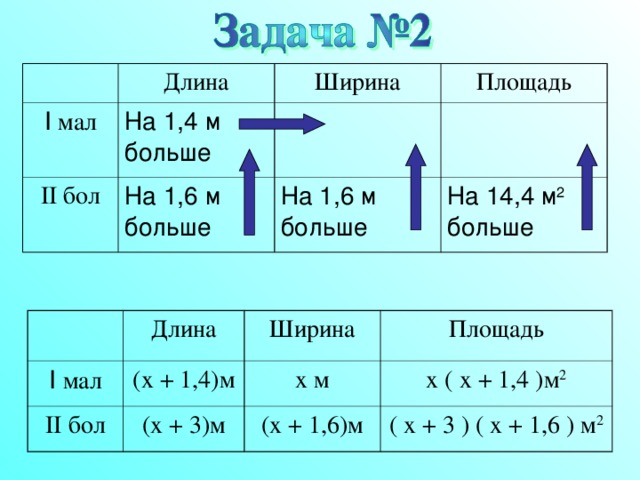
Длина
I мал
Ширина
На 1,4 м больше
II бол
Площадь
На 1,6 м больше
На 1,6 м больше
На 14,4 м 2 больше
Длина
I мал
Ширина
II бол
( x + 1,4) м
Площадь
x м
( x + 3) м
x ( x + 1,4 ) м 2
(x + 1,6) м
( x + 3 ) ( x + 1,6 ) м 2
I мал
Длина
( x + 1,4) м
II бол
Ширина
Площадь
x м
( x + 3) м
x ( x + 1,4 ) м 2
(x + 1,6) м
( x + 3 ) ( x + 1,6 ) м 2
(x + 3 ) ( x + 1,6 ) – x ( x + 1,4 ) = 14,4;
x 2 + 1,6x + 3x + 4,8 – x 2 – 1,4x = 14,4;
3,2x = 9,6;
x = 9,6 : 3,2;
x = 3.
1) 3 + 1,4 = 4,4 ( м )
3м и 4,4м.

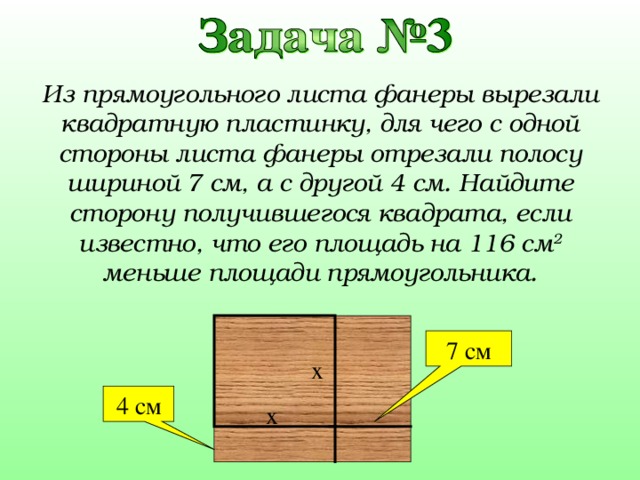
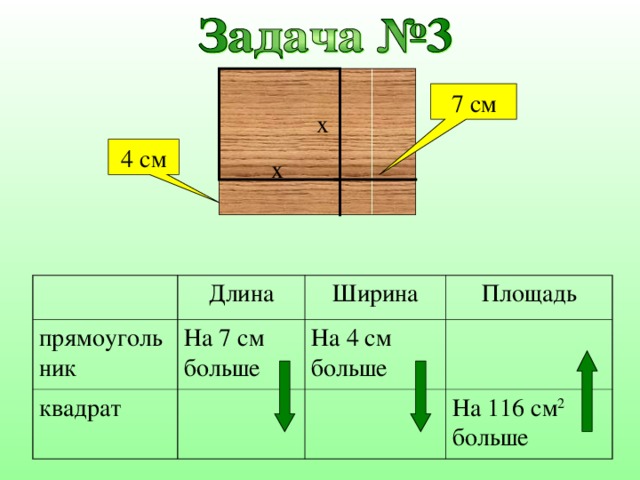
Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 7 см, а с другой 4 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 116 см 2 меньше площади прямоугольника.
7 см
x
4 см
x
7 см
x
4 см
x
прямоугольник
Длина
квадрат
Ширина
На 7 см больше
Площадь
На 4 см больше
На 116 см 2 больше
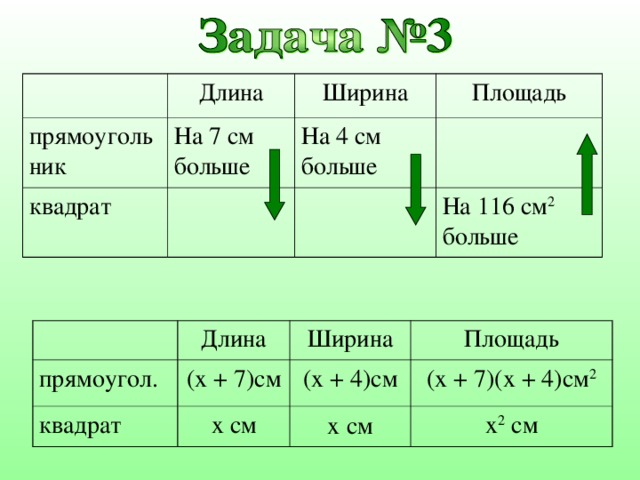
Длина
прямоугольник
Ширина
На 7 см больше
квадрат
Площадь
На 4 см больше
На 116 см 2 больше
прямоугол .
Длина
Ширина
квадрат
( x + 7) см
Площадь
(x + 4) см
x c м
(x + 7)(x + 4) см 2
x см
x 2 см

Длина
прямоугол .
Ширина
( x + 7) см
квадрат
x c м
Площадь
(x + 4) см
(x + 7)(x + 4) см 2
x см
x 2 см
(x + 7)(x + 4) – x 2 = 116;
x 2 + 4x + 7x + 28 – x 2 = 116;
11x = 88;
x = 8.
8 см.

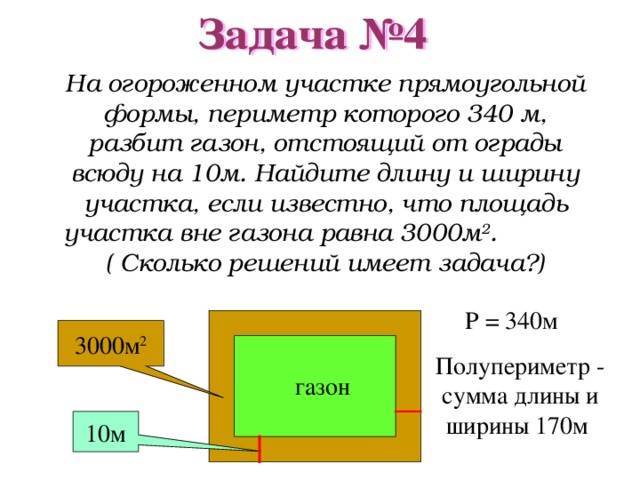
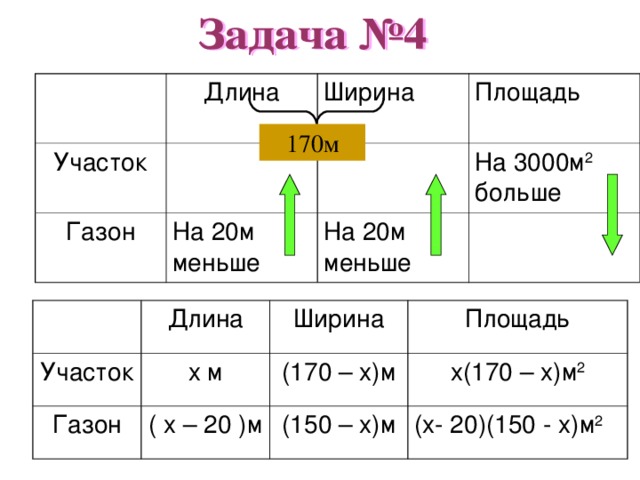
На огороженном участке прямоугольной формы, периметр которого 340 м, разбит газон, отстоящий от ограды всюду на 10м. Найдите длину и ширину участка, если известно, что площадь участка вне газона равна 3000м 2 . ( Сколько решений имеет задача?)
P = 340 м
3000м 2
Полупериметр - сумма длины и ширины 170м
газон
10м

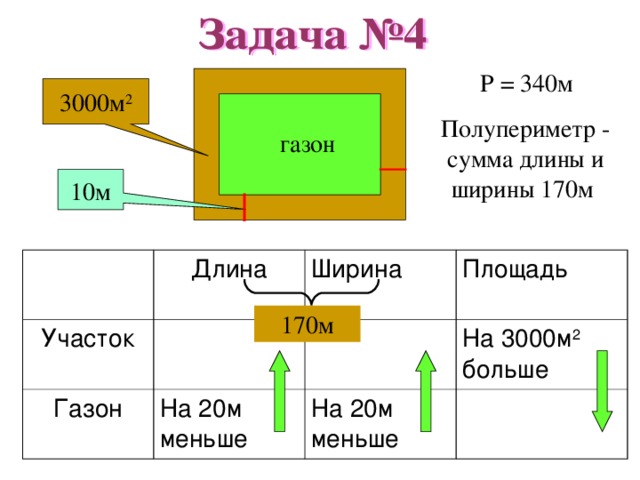
P = 340 м
3000м 2
Полупериметр - сумма длины и ширины 170м
газон
10м
Длина
Участок
Газон
Ширина
Площадь
На 20м меньше
На 3000м 2 больше
На 20м меньше
170м

Длина
Участок
Ширина
Газон
Площадь
На 20м меньше
На 3000м 2 больше
На 20м меньше
170м
Длина
Участок
Ширина
Газон
x м
Площадь
(170 – x) м
( x – 20 ) м
x(170 – x) м 2
(150 – x) м
(x- 20)(150 - x) м 2

Длина
Участок
Ширина
x м
Газон
Площадь
(170 – x) м
( x – 20 ) м
x(170 – x) м 2
(150 – x) м
(x- 20)(150 - x) м 2
x(170 – x) – (x – 20)(150 – x) = 3000;
170x – x 2 – (150x – x 2 – 3000 + 20x) = 3000;
170x – x 2 – 150x + x 2 + 3000 – 20x = 3000;
0x = 0;
Бесконечно много решений, но 20

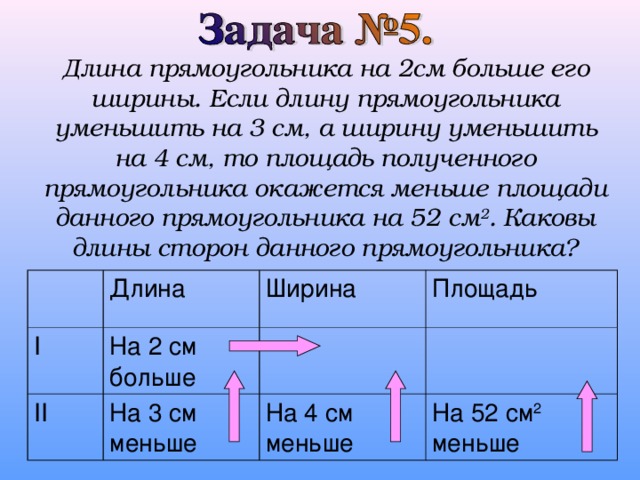
Длина прямоугольника на 2см больше его ширины. Если длину прямоугольника уменьшить на 3 см, а ширину уменьшить на 4 см, то площадь полученного прямоугольника окажется меньше площади данного прямоугольника на 52 см 2 . Каковы длины сторон данного прямоугольника?
Длина
I
Ширина
II
На 2 см больше
Площадь
На 3 см меньше
На 4 см меньше
На 52 см 2 меньше

Длина
I
Ширина
На 2 см больше
II
Площадь
На 3 см меньше
На 4 см меньше
На 52 см 2 меньше
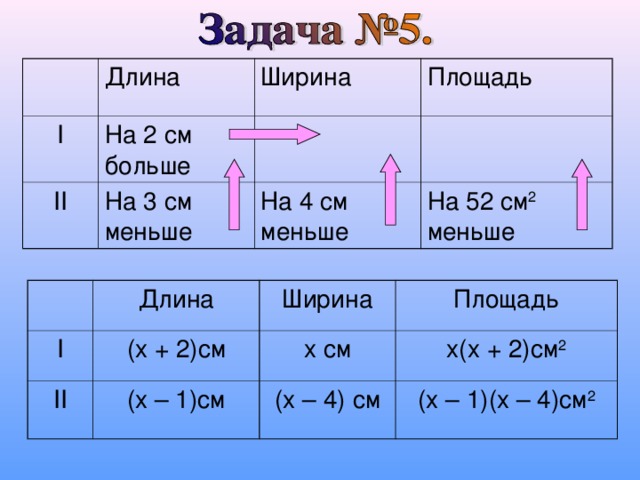
Длина
I
Ширина
II
(x + 2) см
Площадь
x см
( x – 1)см
x(x + 2) см 2
(x – 4) см
(x – 1)(x – 4) см 2

Длина
I
Ширина
(x + 2) см
II
Площадь
x см
( x – 1)см
x(x + 2) см 2
(x – 4) см
(x – 1)(x – 4) см 2
x(x + 2) – (x – 1)(x – 4) = 52;
x 2 + 2x – (x 2 – 4x – x + 4) = 52;
x 2 + 2x – x 2 + 4x + x – 4 = 52;
7x = 56;
x = 8. 1) 8 + 2 = 10.
Ответ.
Длина 10см,
Ширина – 8см.

На дом.
Длина прямоугольника на 10 см больше ширины. Если его длину увеличить на 3 см, а ширину уменьшить на 2 см, то площадь получившегося прямоугольника окажется на 14 см 2 меньше площади данного прямоугольника. Найдите стороны данного прямоугольника.


 Получите свидетельство
Получите свидетельство Вход
Вход

































































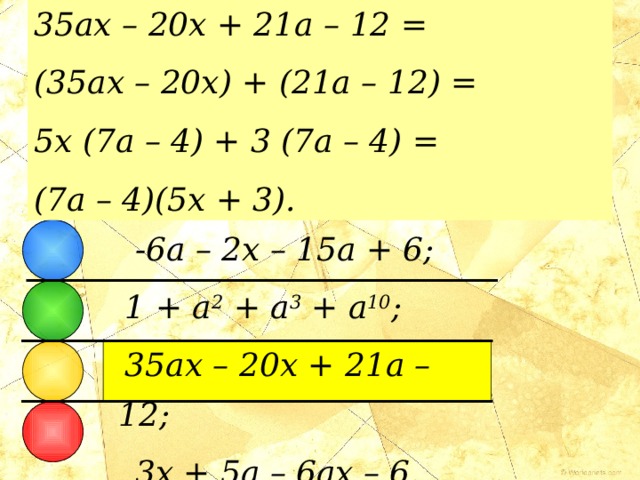















































 Многочлены (5.69 MB)
Многочлены (5.69 MB)
 0
0 1165
1165 183
183 Нравится
0
Нравится
0


