Методическая разработка урока геометрии в 9 классе "Площадь кругового сектора"

Тема: "Площадь кругового сектора"

Цели: ввести понятие кругового сектора, вывести формулу для вычисления площади кругового сектора; рассмотреть круговой сегмент, научить применять знания при решении задач; способствовать развитию логического мышления.

Оборудование: задания-карточки, таблица, картинки

Ход урока.

1. Организационная часть.

2.Устные упражнения:

Девиз урока: "Учитесь, читайте, размышляйте и извлекайте из всего самое полезное" (Н.И.Пирогов - русский хирург, основоположник военно-полевой хирургии)

3. Актуализация опорных знаний учащихся.

Математический диктант:

1)Что такое окружность? (Фигура, состоящая из множества точек плоскости, равноудаленных от центра)

2) Радиус окружности? (Отрезок соединяющий центр окружности с любой точкой окружности)

3) Чему равна длина окружности? (L=2ПR, где П=3,14….)

4)Что такое круг? (часть плоскости, ограниченная окружностью)

5) Чему равна площадь круга? Формула площади круга. (S=ПR²)

4. Изучение нового материала.

У каждого из нас на руках геометрическая фигура, которая называется круговым сектором. (Сложить все секторы вместе и получается круг). Прежде всего мы должны дать ему строгое математическое определение и вывести формулу для его вычисления.

Итак записываем тему урока.

1. Ввести понятие кругового сектора и понятие дуги сектора. Показать примеры круговых секторов на циферблате часов, на барабане у Якубовича. (Работа по учебнику)

2. Вывести формулу для вычисления площади кругового сектора радиуса R, ограниченного дугой окружности с градусной мерой .

Т.к. площадь всего круга равна , то площадь кругового сектора, ограниченного дугой в 1 , равна .Поэтому площадь S выражается формулой

3. Ввести понятие кругового сегмента. Рассмотреть площадь кругового сегмента (на ознакомительном уровне).

5. Закрепление изученного материала. Решение задач.

1. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 40⁰ . ( см²)

2. Площадь кругового сектора равна 24 м² , если его центральный угол равен 50⁰. Найдите радиус сектора. ( )

3. Площадь кругового сектора равна см², его радиус равен 3м. Чему равен центральный угол? (20⁰)

4.Решить задачу №1128 (по учебнику)

5

А

В

6. Задачи ОГЭ

Задание 17 № 169888

Найдите пло­щадь кругового сектора, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, а угол сек­то­ра равен 120°. В от­ве­те укажите площадь, деленную на π. 

Ответ: 27.

Задание 877

Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.

Решение задачи: Центральный угол равен 60°, следовательно, градусная мера дуги, на которую он опирается, тоже равна 60°. Градусная мера всего круга равна 360°. Следовательно, площадь сектора составляет 60°/360°=1/6 часть от площади круга. Тогда, площадь сектора равна 78/6=13. Ответ: 13

В прямоугольном треугольнике с катетами 5 и 12 см найдите радиус окружности (в см), описанной около этого треугольника. (рис. на слайде)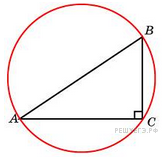

- Что надо знать, чтобы вычислить радиус окружности?

(Где находится центр описанной около прямоугольного треугольника окружности).

- центр описанной около прямоугольного треугольника окружности является серединой его гипотенузы. Значит надо найти гипотенузу по теореме Пифагора.

Решение. 1) D = с =  =  = = 13 (см)

1. R = D: 2 = 13:2 = 6,5 (см).

Ответ: 6, 5 см.

IV. Самостоятельная работа (использованы задания образовательного портала «Решу ЕГЭ»)

Вариант 1.

За­да­ние 1. ABCD — квадрат, BC=20 мм, на сторонах квадрата AB и AD построены полукруги. Вычисли площадь полученной фигуры (π≈3).

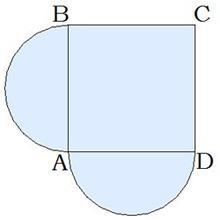
Задача 2.

№ 27897. Ра­ди­ус окруж­но­сти, опи­сан­ной около пря­мо­уголь­но­го тре­уголь­ни­ка, равен 4. Най­ди­те ги­по­те­ну­зу этого тре­уголь­ни­ка.

По­яс­не­ние. Впи­сан­ный угол, опи­ра­ю­щий­ся на диа­метр окруж­но­сти, яв­ля­ет­ся пря­мым, зна­чит,  – диа­метр.   Ответ: 8.

Задача № 3.

За­да­ние 15 № 245008. 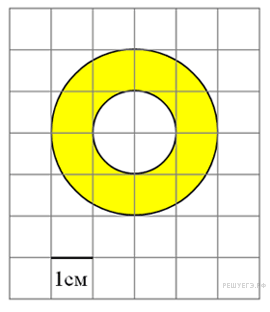 Най­ди­те (в см²) пло­щадь  коль­ца, изоб­ра­жен­ного на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). В от­ве­те за­пи­ши­те  .

Решение

Пло­щадь коль­ца равна раз­но­сти пло­ща­ди боль­шо­го и ма­ло­го кру­гов. Ра­ди­ус боль­шо­го круга равен 2, а ма­ло­го — 1, от­ку­да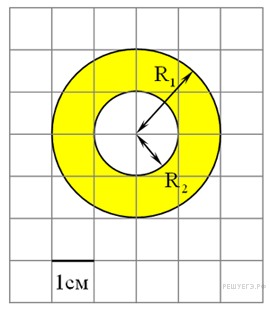

  .

. Ответ: 3.

Вариант 2.

Задание 1.

Вычисли площадь сектора, если радиус круга равен 3см и центральный угол сектора равен 216°.  π≈3

За­да­ние2.  

№ 27896. Ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равна 12. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

Решение. Впи­сан­ный угол опи­ра­ю­щий­ся на диа­метр окруж­но­сти, яв­ля­ет­ся пря­мым, зна­чит,  – диа­метр.

   Ответ: 6.

Задание № 3.

За­да­ние 15 № 27642. Най­ди­те пло­щадь коль­ца, огра­ни­чен­но­го кон­цен­три­че­ски­ми окруж­но­стя­ми, ра­ди­у­сы ко­то­рых равны  и  .

По­яс­не­ние. Пло­щадь круга опре­де­ля­ет­ся фор­му­лой S = πR². Пло­щадь коль­ца равна раз­но­сти пло­ща­дей пер­во­го и вто­ро­го круга. Тогда  ,    По­это­му пло­щадь коль­ца: S = S₁ − S₂ = 16 − 4 = 12.  Ответ: 12.

7. Проверка усвоения темы. Тест(5 мин). Работы оцениваются по желанию детей.

1 вариант.

1

А

А) один В) два С) не знаю

В

2. Каждому элементу первого столбца соотнесите соответствующую формулу из второго столбца:

А) площадь треугольника 1)

В) площадь кругового сектора 2)

С) площадь круга 3)

3. Вычислите площадь круга, радиус которого равен 3 см.

А) В) С) D) не знаю

4. Найдите площадь кругового сектора, если радиус круга равен 6см, а его центральный угол равен 60⁰.

А) В) С) D)

5. Площадь кругового сектора равна м², его центральный угол равен 40⁰. Найдите радиус данного сектора.

А) 162м В) м С)81м D) м

2 вариант.

1.Назовите сектор, у которого центральный угол равен 360- .

А) сектор с дугой AMN

В) сектор с дугой ANB

С) такого сектора нет

2. Каждому элементу первого столбца соотнесите соответствующую формулу из второго столбца:

А) площадь круга 1)

В) площадь квадрата 2)

С) площадь кругового сектора 3) S=

3. Вычислите площадь круга, диаметр которого равен 8дм.

А) В) С) D) не хватает данных

4. Найдите площадь кругового сектора, если радиус равен 12м, а его центральный угол равен 30⁰.

А) В) С) D)

5. Площадь кругового сектора равна м², его радиус равен 6м. Найдите центральный угол данного сектора.

А) 10 ⁰ В) 36⁰ С)100⁰ D)120⁰

Взаимопроверка.

Ответы:1вариант 2 вариант

1. В 1. В

2. 312 2. 231

3. С 3. С

4. А 4. В

5. D 5. С

6.Итог урока. Оценки.

7. Домашнее задание. П111, 112 Вопросы 1-12, №№1126 КИМ в3 №9-13