Оборудование. Образец из стали, алюминия и графита, катушка с током, железный сердечник
Цель. Научиться вычислять магнитные поля в магнетиках и изучить различные свойства магнетиков.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Вам уже известно, что на кусок железа, помещенный близи катушки с током, действует значительная сила притяжения. Известно также, что сила взаимодействия между двумя катушками с током существенно возрастает, если поместить в них железный сердечник. Аналогичными свойствами обладают, кроме железа, различные сорта стали, а также никель, кобальт и некоторые сплавы:
п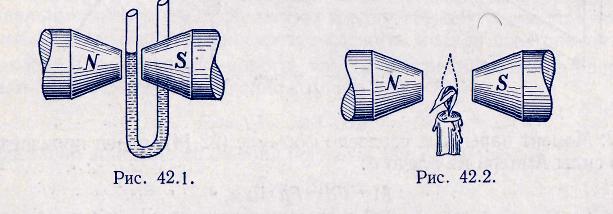 ермаллои, альни, магнико.
ермаллои, альни, магнико.
Все эти вещества называются
ферромагнетиками (от латинского ferrum — железо).
По интенсивности взаимодействия с магнитным полем можно все вещества разбить на два класса. К слабо магнитным веществам относятся все диамагнетики и парамагнетики. Эти вещества при любых температурах очень слабо взаимодействуют с магнитным полем. сильно магнитным веществам относятся ферромагнетики и антиферромагнетики, которые при определенных температурах сильно взаимодействуют с полем.
2. Парамагнетиками называются вещества, которые втягиваются в область более сильного поля. Если в U-образную стеклянную трубку налить парамагнитную жидкость и поместить одно колено между полюсами сильного электромагнита, то жидкость в этом колене поднимется (рис. 42.1). Стерженек из парамагнитного вещества, подвешенный на тонкой нити, ориентируется в магнитном поле вдоль силовых линий.
По своим свойствам парамагнетики несколько напоминают ферромагнетики, но сила их взаимодействия полем в сотни и тысячи раз слабее. Поэтому для наблюдения парамагнитных эффектов необходимы сильные магнитные поля. Парамагнитными свойствами обладают платина, алюминий, вольфрам, все щелочные и щелочно-земельные металлы; из газов — кислород и в слабой степени окись азота.
3. Диамагнетиками называются вещества, которые выталкиваются из магнитного поля. Так, если между полюсами электромагнита зажечь свечу, то пламя вытолкнется из поля (рис. 42.2). Стерженек из диамагнитного вещества, подвешенный на нити в сильном магнитном поле, устанавливается поперек
силовых линий. Заметим, что силы, действующие на диамагнетик в магнитном поле, на один-два порядка меньше сил, действующих на парамагнетик в этом же поле. Поэтому для наблюдения диамагнитных эффектов требуются очень сильные поля. К диамагнетикам относятся почти все газы (кроме кислорода), вода, серебро, золото, медь, алмаз, графит, висмут, многие органические соединения.
Магнитный момент атома.В начале XIX в. Ампер пришел к выводу, что магнитные свойства вещества можно объяснить, если допустить, что атомы представляют собой микроскопические элементарные магниты. Однако обосновать происхождение элементарных магнитных моментов Ампер не смог. Ядерная модель строения атома, которой мы уже пользовались для объяснения механизма деформационной поляризуемости (§ 38.5), поможет нам понять происхождение магнитных моментов атомов. В самом деле, электрон, циркулируя в атоме, представляет собой элементарный ток, обладающий магнитным моментом рорб. Кроме того, циркулирующий по орбите электрон имеет момент импульса, называемый орбитальным моментом
импульса Lop6. Согласно (40.28) между этими величинами должна существовать следующая связь: Pmорб=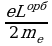 Здесь те — масса покоя электрона, е — его заряд. Магнитный момент атома складывается из магнитных моментов электронов, движущихся вокруг ядра, и магнитного момента самого ядра. Однако опыт показывает, что магнитный момент ядра примерно в 2000 раз меньше магнитного момента электрона (§ 80.2). Поэтому при изучении магнитных свойств вещества пренебрегают магнитным моментом ядра и считают, что магнитный момент атома равен векторной сумме магнитных моментов электронов, циркулирующих вокруг ядра. Попытаемся оценить величину этого магнитного момента. Пусть в пространстве выделено некоторое направление, например ось г. Это может означать, что вдоль этой оси направлено какое-либо магнитное поле. В квантовой механике доказывается, что проекция орбитального момента импульса на заданное направление может принимать только некоторые, вполне определенные значения:
Здесь те — масса покоя электрона, е — его заряд. Магнитный момент атома складывается из магнитных моментов электронов, движущихся вокруг ядра, и магнитного момента самого ядра. Однако опыт показывает, что магнитный момент ядра примерно в 2000 раз меньше магнитного момента электрона (§ 80.2). Поэтому при изучении магнитных свойств вещества пренебрегают магнитным моментом ядра и считают, что магнитный момент атома равен векторной сумме магнитных моментов электронов, циркулирующих вокруг ядра. Попытаемся оценить величину этого магнитного момента. Пусть в пространстве выделено некоторое направление, например ось г. Это может означать, что вдоль этой оси направлено какое-либо магнитное поле. В квантовой механике доказывается, что проекция орбитального момента импульса на заданное направление может принимать только некоторые, вполне определенные значения:
Lорбz = mh,
где h — постоянная Планка, т — целое число. Пользуясь соотношением (42.1), получим для проекции орбитального магнитного момента, которую мы обозначим :
Pорьmz=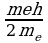 =m
=m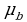 Величина
Величина 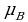 называется магнетоном Бора. Она составлена из мировых констант — заряда и массы электрона и постоянной Планка — и поэтому тоже является мировой константой.
называется магнетоном Бора. Она составлена из мировых констант — заряда и массы электрона и постоянной Планка — и поэтому тоже является мировой константой.
Магнетон Бора — это минимальное отличное от нуля значение проекции магнитного момента электрона на произвольное направление. А так как магнитный момент атома есть векторная сумма магнитных моментов электронов, то мы можем утверждать, что проекция магнитного момента атома на некоторую ось либо равна нулю, либо кратна магнетону Бора. Ниже мы увидим, что опыты подтверждают эту оценку.
Величины, характеризующие магнитное поле в веществе
1. Для характеристики степени поляризации диэлектрика в электрическом поле была введена особая физическая величина — вектор поляризации, равный дипольному моменту единицы объема поляризованного диэлектрика. Аналогично введем величину, характеризующую степень намагниченности вещества в магнитном поле,— вектор намагниченности. Вектором намагниченности М называется магнитный момент единицы объема намагниченного вещества. Чтобы его вычислить, необходимо найти векторную сумму магнитных моментов всех атомов, заключенных в единице объема намагниченного вещества. Для простоты рассуждений положим, что вещество однородное и все его атомы имеют один и тот же магнитный момент рт. Тогда вектор намагниченности
M=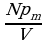 =npm где п — концентрация атомов. Единица намагниченности совпадает с единицей напряженности магнитного поля: А/м=[H].
=npm где п — концентрация атомов. Единица намагниченности совпадает с единицей напряженности магнитного поля: А/м=[H].
2. Ограничимся рассмотрением простейшего случая, когда однородное и изотропное вещество сплошь заполняет магнитное поле. Это можно реализовать, если на тороидальный сердечник из исследуемого вещества равномерно намотать обмотку, по которой течет ток. Вещество сердечника, естественно, намагнитится за счет действия магнитного поля тока. Оказывается, что если вещество представляет собой парамагнетик или диамагнетик, то его вектор намагниченности пропорционален напряженности намагничивающего поля
М = ктН. (42.6)
Коэффициент пропорциональности хт в выражении (42.6) называется магнитной восприимчивостью вещества. Читатель легко убедится, что магнитная восприимчивость является безразмерной величиной.
3. Вектор намагниченности определяет индукцию магнитного поля Bвещ, создаваемого намагниченным веществом. По аналогии с тем, как связана индукция поля токов с напряженностью этого поля (BTOK=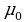 H), напишем соотношение между индукцией поля вещества и его намагниченностью:Bвещ=
H), напишем соотношение между индукцией поля вещества и его намагниченностью:Bвещ=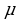 0M. Индукция магнитного поля в веществе, которое сплошь заполняет магнитное поле, представляет собой векторную сумму индукций поля намагничивающих токов и поля намагниченного вещества:
0M. Индукция магнитного поля в веществе, которое сплошь заполняет магнитное поле, представляет собой векторную сумму индукций поля намагничивающих токов и поля намагниченного вещества:
В = Вток +Ввещ =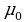 (Н+М). На основании имеем B=
(Н+М). На основании имеем B=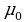 (H+
(H+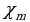 H)=
H)=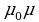 H
H
Величина
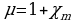
называется магнитной проницаемостью вещества.
Диамагнетизм П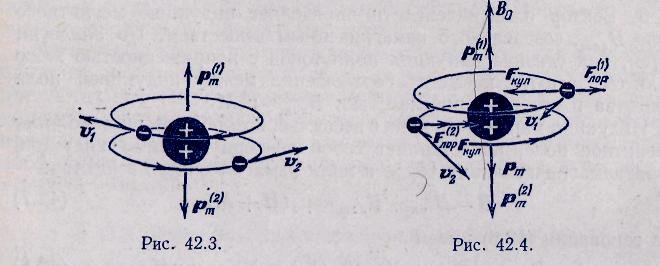 опытаемся выяснить механизм диамагнитного эффекта. Для
опытаемся выяснить механизм диамагнитного эффекта. Для
анализа используем модель атома гелия. Ядро этого атома имеет заряд q=+2e, а вокруг ядра обращаются два электрона. Опыт показывает, что атом гелия не имеет магнитного момента. Это можно объяснить, если мы предположим, что оба электрона обращаются вокруг ядра с одинаковой скоростью по одинаковым орбитам, но в противоположных направлениях. Тогда их орбитальные магнитные моменты будут равны по величине, но противоположны по знаку,
и суммарный магнитный момент атома окажется равным нулю (рис. 42.3).Поместим атом гелия в магнитное поле с индукцией В0=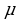 0Н. Для простоты рассуждений положим, что вектор индукции перпендикулярен плоскости орбиты электрона (рис. 42.4). В этом случае
0Н. Для простоты рассуждений положим, что вектор индукции перпендикулярен плоскости орбиты электрона (рис. 42.4). В этом случае
на электрон действуют две силы — кулоновская сила притяжения к ядру и сила Лоренца. Их равнодействующая сообщает электрону центростремительное ускорение. Уравнения движения для обоих электронов примут вид
Fкул- Fлор= 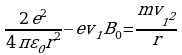
Следует обратить внимание на тот факт, что в этих уравнениях мы полагаем, что под действием магнитного поля меняется только скорость движения электрона, но не радиус орбиты.
3. Из уравнений (42.10) следует, что под действием магнитного поля скорость движения первого электрона уменьшилась, второго возросла. Соответственно изменяются и их магнитные моменты. Таким образом, под действием внешнего магнитного поля у атома наводится (индуцируется) магнитный момент
Pm=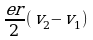
Заметим, что индуцированный магнитный момент рт направлен противоположно направлению вектора индукции внешнего поля (рис. 42.4). Разность скоростей найдем из (42.10), если вычтем из нижнего равенства верхнее:
eB0(v2 + v1) =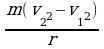
или после сокращений
v2-v1=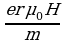 (42.12)
(42.12)
Подставив в (42.11), получим для индуцированного магнитного момента
(42.13)
Учитывая, что векторы рт и Н направлены противоположно, перепишем (42.13) в векторном виде:
Рт=-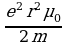 Н
Н
.4. Вектор намагниченности, согласно (42.5), равен
M=npm=-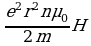
Итак, здесь вектор намагниченности действительно пропорционален напряженности намагничивающего поля (см. (42.6)). Магнитная восприимчивость является отрицательной величиной:
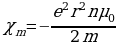
Парамагнетизм.
1. Рассмотренный в предыдущем параграфе механизм намагничивания диамагнетиков сводится к наведению дополнительного магнитного момента у атома под действием внешнего магнитного поля. Это явление характерно для атомов любого вещества, следовательно, все вещества должны обладать диамагнитными свойствами. Откуда же берутся парамагнетики?
Оказывается, что в отличие от диамагнетиков, у которых магнитные моменты электронов внутри атома скомпенсированы, атомы парамагнетиков имеют не скомпенсированные магнитные моменты. Под действием внешнего магнитного поля эти магнитные моменты поворачиваются, стремясь расположиться вдоль силовых линий поля. Тепловое движение, естественно, расстраивает этот порядок. Мы видим, что механизм намагничивания парамагнетиков вполне аналогичен механизму поляризации диэлектриков с полярными молекулами (§ 38.6). Если провести такие же рассуждения, как и при выводе формулы (38.25), получим выражение для намагниченности парамагнетиков:
M=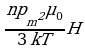
Магнитная восприимчивость парамагнетиков является положительной величиной:
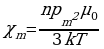
Как видно, при неизменной концентрации атомов (т. е. при неизменной плотности вещества) магнитная восприимчивость парамагнетиков меняется обратно пропорционально абсолютной температуре(закон Кюри):
xm=const/T
Это явление подтверждается экспериментально.
Заметим, что выражение (42.16) справедливо при условии, если pmB0/kT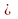 .l, т. е. если энергия диполя
.l, т. е. если энергия диполя 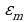 магнитном поле
магнитном поле 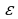 т=ртВ0 много меньше энергии теплового движения частицы R=kT. Поскольку pm=9,27-10~24 А-м2, а максимально достижимая индукция магнитного поля Вмаксда 1,3 Тл, то при комнатных температурах это условие всегда выполняется. Лишь при очень низких температурах можно получить
т=ртВ0 много меньше энергии теплового движения частицы R=kT. Поскольку pm=9,27-10~24 А-м2, а максимально достижимая индукция магнитного поля Вмаксда 1,3 Тл, то при комнатных температурах это условие всегда выполняется. Лишь при очень низких температурах можно получить
pmBu/kT= 1;
для этого парамагнетик следует охладить до температуры T=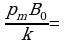
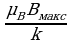 =1K
=1K
 т. е. близкой к абсолютному нулю. В этом случае намагниченность парамагнетика будет близка к насыщению, так как все магнитные моменты атомов расположатся вдоль поля, а слабое тепловое движение этот порядок разрушить не сможет.
т. е. близкой к абсолютному нулю. В этом случае намагниченность парамагнетика будет близка к насыщению, так как все магнитные моменты атомов расположатся вдоль поля, а слабое тепловое движение этот порядок разрушить не сможет.
Ферромагнетизм. Точка Кюри.
1. В отличие от парамагнетиков и диамагнетиков, у которых вектор намагниченности пропорционален напряженности намагничивающего поля, у ферромагнетиков намагниченность является весьма сложной нелинейной функцией напряженности! Для никеля эта зависимость изображена на рис. 42.5. Для удобства изображения масштаб нарушен: область напряженности поля от 0,1-103 до 2-103 А/м растянута. Как видно из рисунка, намагниченность никеля сначала быстро нарастает с ростом напряженности магнитного поля. Затем наступает магнитное насыщение, когда намагниченность уже 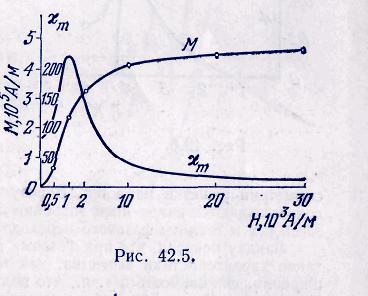 от величины намагничивающего поля.
от величины намагничивающего поля.
Поскольку намагниченность ферромагнетика не пропорциональна напряженности намагничивающего поля, выражения (42.6) и (42.8) теряют смысл. Формально, однако, ими можно пользоваться, учитывая, что для ферромагнетиков магнитная восприимчивость
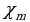 =М/H
=М/H
и магнитная проницаемость 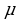 =В/
=В/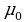 H являются не посто намагничивающего поля.
H являются не посто намагничивающего поля.
2. Следующее важное отличие ферромагнетиков заключается в том, что если парамагнитные или диамагнитные свойства вещества проявляются в любом агрегатном состоянии, то ферромагнитные свойства наблюдаются только у кристаллов. В жидком или газообразном состоянии ферромагнитные вещества ведут себя как обычные парамагнетики. Отсюда следует, что ферромагнитные свойства некоторых веществ определяются не особыми свойствами их атомов — последние ничем не отличаются от атомов парамагнетиков,— а особой структурой их кристаллической решетки. При изменении структуры решетки должны меняться и магнитные свойства ферромагнетиков. Опыт подтверждает это предположение.
Оказывается, что для каждого ферромагнетика имеется определенная температура — точка Кюри, выше которой ферромагнитные свойства исчезают и вещество становится обычным парамагнетиком. Для железа точка Кюри составляет 770 °С, для никеля 360°С, а для пермаллоя (сплав 70% Fe и 30% №) всего лишь 70 °С.4. Как показал Л. Д. Ландау, точка Кюри у ферромагнетиков — это температура фазового перехода второго рода.
При фазовых переходах первого рода меняется структура вещества; например, при плавлении кристалла дальний порядок меняется на ближний. В результате меняется внутренняя энергия и энтропия тела, что требует затраты некоторой энергии — теплоты фазового перехода (см. гл. 36). Фазовые переходы второго рода, например исчезновение ферромагнитных свойств вещества при переходе через точку Кюри, не сопровождаются изменением агрегатного состояния. В частности, при этом кристаллическая решетка не разрушается, хотя тип симметрии решетки меняется. В результате фазовые переходы второго рода не сопровождаются изменением энтропии и внутренней энергии тела, следовательно, здесь нет и теплоты фазового перехода.
Ландау показал, что при фазовых переходах второго рода скачком меняются такие характеристики вещества, как теплоемкость, коэффициент теплового расширения, сжимаемость и т. п., что подтверждается экспериментом. На рис. 42.6 показаны графики изменения намагниченности и теплоемкости некоторого вещества. Как видно, при температуре 4,2 К намагниченность резко падает; следовательно, эта температура есть точка Кюри для данного вещества. При этой температуре теплоемкость вначале быстро возрастает, а затем падает.
3. Ферромагнетизм присущ только кристаллам, а последние обладают анизотропией, поэтому монокристалл ферромагнитного вещества должен обладать анизотропией намагничивания — его магнитные свойства должны быть разными в разных направлениях. Опыт подтверждает это предположение.
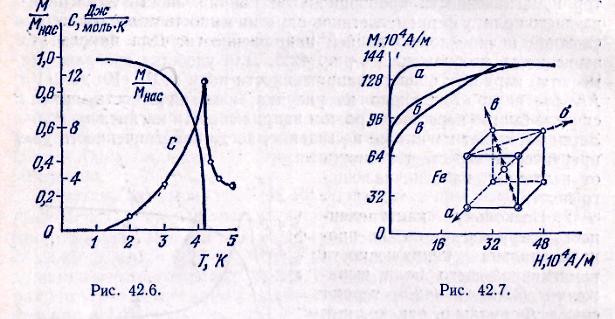
Н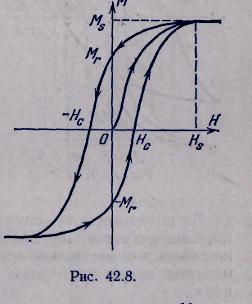 а рис. 42.7 изображены графики намагниченности монокристалла железа, имеющего решетку типа объемно-центрированного куба. Оказывается, что в направлении ребра куба намагниченность вещества при данном значении напряженности поля наибольшая (а), меньше она в направлении диагонали грани (б) и наименьшая намагниченность — в направлении пространственной диагонали куба (б). Поэтому ребро куба называется направлением легкого намагничивания, а диагональ куба — направлением трудного намагничивания. Естественно, что в поликристалле анизотропия намагниченности не проявляется, поскольку отдельные микрокристаллики ориентированы беспорядочно.
а рис. 42.7 изображены графики намагниченности монокристалла железа, имеющего решетку типа объемно-центрированного куба. Оказывается, что в направлении ребра куба намагниченность вещества при данном значении напряженности поля наибольшая (а), меньше она в направлении диагонали грани (б) и наименьшая намагниченность — в направлении пространственной диагонали куба (б). Поэтому ребро куба называется направлением легкого намагничивания, а диагональ куба — направлением трудного намагничивания. Естественно, что в поликристалле анизотропия намагниченности не проявляется, поскольку отдельные микрокристаллики ориентированы беспорядочно.
Гистерезис.
1. Характерным свойством ферромагнетиков является гистерезис. Явление заключается в том, что намагниченность ферромагнетика зависит не только от напряженности намагничивающего поля в данный момент, но и от предварительного намагничивания образца. Поэтому вообще нельзя указать, какая намагниченность ферромагнетика, соответствует данному значению
напряженности намагничивающего поля, если не известно, в каком состоянии он до этого находился. То же, естественно, относится к значениям магнитной восприимчивости и проницаемости.
График рис. характеризует ход первоначальной намагниченности, когда ферромагнетик был сначала нагрет выше точки Кюри и тем самым полностью размагничен, а затем охлажден и подвергнут намагничиванию. Совершенно иной вид будет иметь кривая намагниченности, если ферромагнетик был уже ранее намагничен.
2. Изготовим сердечник в форме тороида из размагниченного ферромагнетика и обмотаем его равномерно проводником, ток в обмотке, мы тем самым меняем напряженность намагничивающего поля. Пусть напряженность поля возрастет до значения Hs (рис. 42.8). Этому значению поля соответствует намагниченность насыщения, равная Ms. Будем уменьшать ток в обмотке, уменьшая тем самым напряженность намагничивающего поля. Мы убедимся, что намагниченность сердечника в процессе размагничивания остается все время большей, чем в процессе намагничивания.
Когда ток в обмотке станет, равен нулю, исчезнет и намагничивающее поле. Но намагниченность ферромагнетика не обратится в нуль — сердечник сохранит некоторую остаточную намагниченность Мг. И только в том случае, когда по обмотке будет пропущен ток обратного направления и возникнет поле с напряженностью Нс., намагниченность сердечника обратится в нуль. Напряженность размагничивающего поля Нс. называется коэрцитивной силой.
Кривая, изображенная на рис. называется гистерезисной петлей.
3. В зависимости от химического состава, а также от характера тепловой и механической обработки материала (закалка, отжиг, прокат, холодная штамповка и т. п.) встречаются ферромагнетики с различными свойствами. Вещества с малыми значениями коэрцитивной силы называются «мягкими» магнитными материалами, высококоэрцитивные материалы — «жесткими». На рис. 42.9 изображены
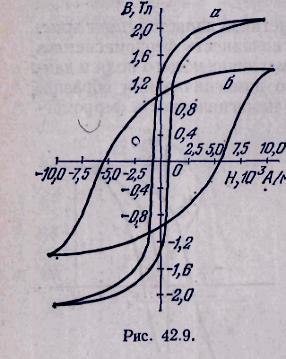 гистерезисные петли двух материалов: магнитно-мягкого железа (а) и высококоэрцитивной закаленной стали (б).
гистерезисные петли двух материалов: магнитно-мягкого железа (а) и высококоэрцитивной закаленной стали (б).
Форма гистерезисной петли определяет область применения того или иного ферромагнетика. «Мягкие» магнитные материалы применяются для изготовления сердечников электромагнитов, где важно иметь большое ' значение максимальной индукции поля и малую коэрцитивную силу.
Магнитно-жесткие материалы используются для изготовления постоянных магнитов. Благодаря большому значению коэрцитивной силы и относительно большой остаточной намагниченности эти магниты могут длительное время создавать сильные магнитные поля.
Постоянные магниты из высококоэрцитивных сплавов применяются в магнитоэлектрических измерительных приборах, в электродинамических репродукторах («динамиках») и микрофонах, в небольших генераторах (например, велосипедных), в микроэлектродвигателях и т. п.
Доменная структура ферромагнетиков1. Особенности ферромагнетиков можно объяснить, следуя классической теории ферромагнетизма, предложенной П. Вейссом. Согласно этой теории, при температурах ниже точки Кюри ферромагнетик состоит из микроскопических областей, называемых доменами, в каждой из которых магнитные моменты атомов расположены строго в одном направлении, соответствующем направлению легкого намагничивания (§ 42.6). Тем самым каждый домен оказывается намагниченным до насыщения независимо от наличия внешнего магнитного поля и от его величины.
Размеры доменов достигают 10~2-10~3 см, вследствие чего их можно наблюдать в микроскоп. Для того чтобы увидеть домены, на полированную поверхность ферромагнетика наносят каплю масла, в которой взвешены мельчайшие частицы ферромагнитного порошка
(метод Акулова — Биттера).
Частицы ферромагнитного порошка концентрируются на границах доменов, где магнитное поле наиболее неоднородно (рис. 42.10).
П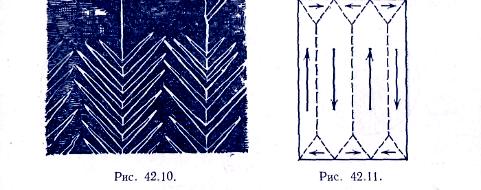 ри отсутствии внешнего магнитного поля домены в монокристалле располагаются так, что их магнитные поля замыкают друг друга и суммарное внешнее магнитное поле оказывается равным нулю.
ри отсутствии внешнего магнитного поля домены в монокристалле располагаются так, что их магнитные поля замыкают друг друга и суммарное внешнее магнитное поле оказывается равным нулю.
На рис. схематически изображены эти домены. Стрелками показаны направления векторов намагниченности внутри доменов. Как показали Л. Д. Ландау и Е. М. Лифшиц, такая система доменов в монокристалле характеризует состояние с минимальной энергией магнитного поля, что с точки зрения законов термодинамики обеспечивает устойчивое равновесие этой системы.
2. Объясним на основе этих представлений механизм намагничивания поликристаллического образца. Поликристалл состоит из отдельных зерен, у которых направления легкого намагничивания ориентированы беспорядочно. Каждое зерно разбивается на несколько доменов, направленных вдоль линии легкого намагничивания (рис. 42.12, а).
П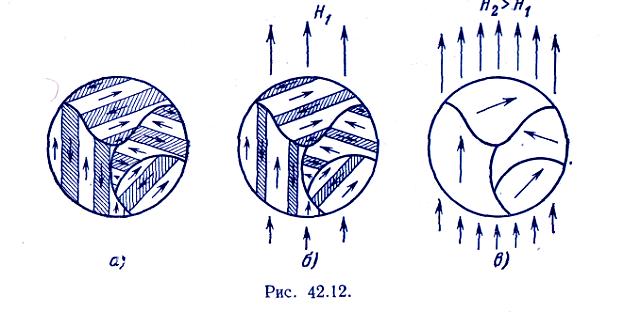 ри включении слабого внешнего магнитного поля всегда найдется множество доменов, у которых направление вектора намагниченности совпадет с направлением внешнего поля. Эти домены будут обладать минимумом энергии и поэтому окажутся в состоянии устойчивого равновесия. Соседние домены обладают максимумом энергии. Поэтому энергетически выгодно, если магнитные моменты некоторых атомов изменят свое направление и присоединятся к тем доменам, энергия которых минимальна. Этот процесс называется смещением границ доменов (рис. 42.12, б).
ри включении слабого внешнего магнитного поля всегда найдется множество доменов, у которых направление вектора намагниченности совпадет с направлением внешнего поля. Эти домены будут обладать минимумом энергии и поэтому окажутся в состоянии устойчивого равновесия. Соседние домены обладают максимумом энергии. Поэтому энергетически выгодно, если магнитные моменты некоторых атомов изменят свое направление и присоединятся к тем доменам, энергия которых минимальна. Этот процесс называется смещением границ доменов (рис. 42.12, б).
По мере роста напряженности внешнего магнитного поля, границы доменов сдвигаются все сильнее. При этом стенки доменов начинают встречать на своем пути дефекты кристалла — дислокации, внедрения и т. п. (§ 32.4). Эти дефекты препятствуют изменению направления магнитного момента у атомов, расположенных вблизи дефекта (препятствуют перемещению стенок домена). По мере роста поля потенциальная энергия атомов (магнитных диполей) вблизи дефекта возрастет настолько, что превысит энергию активации (§ 34.3). В этом случае магнитные моменты атомов вблизи дефекта скачком изменят свое направление на противоположное — иными словами, стенка домена скачком срывается с места и движется до следующего дефекта. Таким образом, процесс намагничивания поликристаллического вещества идет не плавно, а скачками. Это явление называется эффектом Баркгаузена.
Оно может быть обнаружено экспериментально. К пучку из никелевой проволоки подносят магнит; происходит скачкообразное намагничивание никеля, что приводит к скачкообразному изменению магнитного поля. Благодаря явлению электромагнитной индукции (см. гл. 43) в обмотке, навитой на никелевый пучок, возникают импульсы тока, которые хорошо слышны в телефоне.
При уменьшении магнитного поля структура вещества не будет восстанавливаться: домены при размагничивании будут иметь другую форму и ориентировку по сравнению с процессом намагничивания. Это и является причиной гистерезисного эффекта.
3. В достаточно сильных полях все стенки доменов сдвинутся к границам кристаллических зерен, и каждое зерно окажется намагниченным вдоль того направления легкого намагничивания, которое составляет наименьший угол с направлением внешнего поля (рис. 42.12, в). Если еще больше усилить напряженность намагничивающего поля, то магнитные моменты зерен начнут поворачиваться, выстраиваясь вдоль поля. Этот процесс требует сильных полей, в результате чего в этой области намагниченность меняется мало и рост кривой намагничивания замедляется.
Наконец, когда магнитные моменты всех зерен выстроятся вдоль поля, наступает магнитное насыщение — с ростом внешнего поля намагниченность вещества перестает возрастать.
4. Как видно, используя представления о доменной структуре ферромагнетиков, можно объяснить все особенности процесса их намагничивания. Точка Кюри оказывается той температурой, выше которой происходит  разрушение доменной структуры.
разрушение доменной структуры.
Остается ответить на два вопроса. Прежде всего, нужно объяснить, какие силы приводят к тому, что внутри домена магнитные моменты всех атомов самопроизвольно выстраиваются вдоль направления легкого намагничивания. А затем нужно найти причины того, почему одни вещества обладают ферромагнитными свойствами, а другие нет. Ответ на эти вопросы смогла дать только квантовая теория магнитных явлений.
Выполнение работы.
Посчитайте орбитальный магнитный момент и момент импульса.
Определите вектор намагниченности, а также магнитную проницаемость и восприимчивость.
Вычислите температуру образцов в Кельвинах.
Постройте график зависимости вектора намагниченности от напряженности магнитного поля.
Занесите данные в таблицу и сделайте вывод.
Ответьте на контрольные вопросы.
Вариант 1
| Pm | Lорб | m |
| M | n |
| H | B |
|
| r | T |
|
|
| 2 |
|
| 2.7 |
|
| 1.3 |
|
| 0.5 |
|
Контрольные вопросы.
Что называется ферромагнетиками, диамагнетиками, парамагнетиками и вектором намагниченности?
Расскажите о механизме диамагнитного эффекта.
Расскажите о намагниченности парамагнетиков.
Расскажите свойстве ферромагнетиков -гистерезисе. Нарисуйте петлю гистерезиса для жестких и мягких ферромагнетиков.
Расскажите о смещении границ доменов и об эффекте Баркгаузена

 Получите свидетельство
Получите свидетельство Вход
Вход












 Методическая разработка лабораторной работы для студентов 2 курса ФП "Профессионалитет" "Вычисление магнитных полей в магнетиках"о теме (1.3 MB)
Методическая разработка лабораторной работы для студентов 2 курса ФП "Профессионалитет" "Вычисление магнитных полей в магнетиках"о теме (1.3 MB)
 0
0 3
3 0
0 Нравится
0
Нравится
0



