Метод интервалов Новые Имена

Метод интервалов

МОУ СОШ с. Тунгор

Учащиеся: Руденко Дарья

Галюк Анна 11 класс

Учитель: Филонов Л.Н.

Цели и задачи доклада

• Углубленное изучение решения неравенств методом интервалов.
• Разработка и применение алгоритма решения неравенств различного вида с помощью метода интервалов для выполнения типовых заданий при подготовке к ЕГЭ
• Использование как учебное пособие при подготовке к итоговой аттестации

Неравенства. Понятие о методе интервалов ( виды неравенств)

• Линейные неравенства
• Квадратные неравенства
• Рациональные неравенства
• Иррациональные неравенства
• Простейшие неравенства с модулем
• Простейшие показательные неравенства
• Простейшие логарифмические неравенства
• Простейшие тригонометрические неравенства

0 , вместо знака могут быть знаки На числовой оси, внутри области допустимых значений, выделяют интервалы, на которых функция f(x) имеет постоянный знак. Часто концевыми точками таких интервалов являются точки, в которых f(x)= 0 или не определена, т.е. задача о выделении интервалов знакопостоянства сводится в этом случае к решению соответствующих уравнений. Затем определяют знаки на этих интервалах, т.е. у каждого из получившихся интервалов ставят знак плюс или минус в зависимости от того какой знак имеет f(x) на данном интервале, изучают концевые точки и выписывают ответ . " width="640"

Метод интервалов – универсальный метод решения неравенств. Он позволяет найти решение практически для любого вида неравенств.

• Метод интервалов применяют для неравенств вида f(x)0 , вместо знака могут быть знаки
• На числовой оси, внутри области допустимых значений, выделяют интервалы, на которых функция f(x) имеет постоянный знак.
• Часто концевыми точками таких интервалов являются точки, в которых f(x)= 0 или не определена, т.е. задача о выделении интервалов знакопостоянства сводится в этом случае к решению соответствующих уравнений.
• Затем определяют знаки на этих интервалах, т.е. у каждого из получившихся интервалов ставят знак плюс или минус в зависимости от того какой знак имеет f(x) на данном интервале, изучают концевые точки и выписывают ответ .

Одно из наиболее трудных этапов- разложение выражения на линейные множители.

• Вынесение общего множителя. Группировка
• Применение формул сокращенного умножения

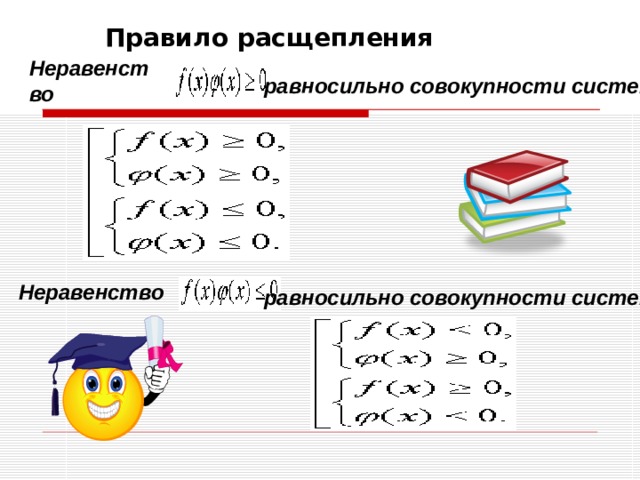
Правило расщепления

Неравенство

равносильно совокупности систем:

Неравенство

равносильно совокупности систем:

Таким образом, при применении правила расщепления неравенств необходимо сначала аккуратно выписать все случаи, когда это неравенство справедливо, т.е. выписать совокупность соответствующих систем неравенств, а затем решить каждую из этих систем и объединить в ответе полученные множества решений.

0, ax + b     решение данных неравенств можно просмотреть как этап при решении квадратных неравенств        " width="640"

Линейные неравенства

Линейными

называются неравенства вида:

ax + b 0, ax + b

решение данных неравенств можно просмотреть как этап при решении

квадратных неравенств     

КВАДРАТНЫЕ НЕРАВЕНСТВА

• Квадратными (строгими и нестрогими) называются неравенства вида

a( x – x1)( x – x2) в соответствии со знаком произведения (– или + )

выбирается ответ

Пример 1.   Решите неравенство  

Пример 1.   Решите неравенство  

Решение:

Решение:

Найдем корни квадратного трехчлена  

Найдем корни квадратного трехчлена  

. 

Далее имеем рисунок № 4

. 

Далее имеем рисунок № 4

Ответ:  

Ответ:  

стоят знаки " width="640"

Сформулируем правило расстановки знаков при решении неравенств вида

На координатную ось наносят числа x 1 ,x 2 ,...,x n , которые разбивают её на интервалы знакопостоянства функции, стоящей в левой части неравенства. В промежутке справа от x n ставят знак “+”, затем, двигаясь справа налево, при переходе через точку x i меняют знак, т.е. левее x n ставят знак ”–”, затем “+” и т.д.

Множество решений неравенства будет

объединение интервалов,

в каждом из которых поставлен знак “+”.

Аналогично может быть описано решение неравенств, в которых вместо знака стоят знаки

Иррациональные неравенства

Пример №2.

Начнём с того, что определим Область Допустимых Значений (ОДЗ) переменной   x .  Ясно, что наличие квадратного корня в неравенстве даст условие:

9x-20 ≥ 0 ,

x ≥ 20/9

Теперь, решим уравнение:

Корни, которого, равны: 4 и 5. Оба корня попадают в ОДЗ нашего неравенства

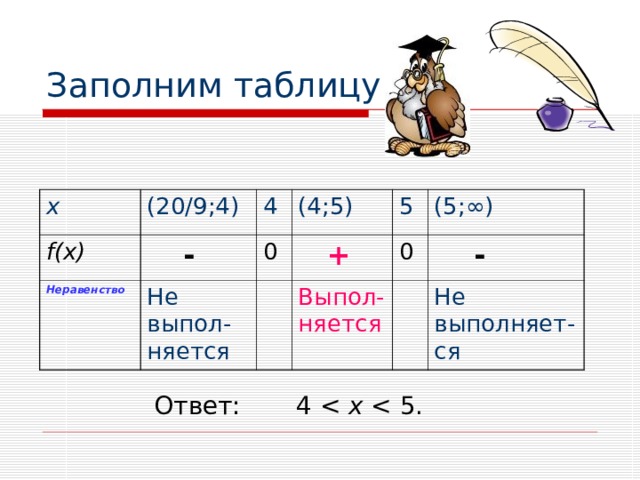
Заполним таблицу

x

(20/9;4)

f(x)

-

4

Неравенство

Не выпол-няется

0

(4;5)

+

5

(5;∞)

Выпол-няется

0

-

Не выполняет-ся

Ответ:       4 x

Простейшие показательные неравенства

.

Пример 3

Решение

Пусть

Тогда после простейших преобразований получаем

Откуда, возвращаясь к переменной x и логарифмируя , имеем:

Ответ:

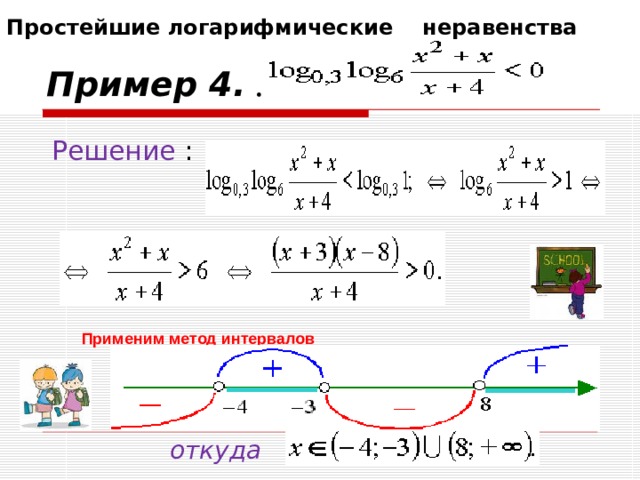
Простейшие логарифмические неравенства

Пример 4. .

.

Решение :

Применим метод интервалов

откуда

Простейшие неравенства с модулем Пример 5

.

Отметим на вещественной оси точки, в которых выраженияпод знаком модуля обращаются в нуль . Таким образом, выделяются интервалы знакопостоянства этих выражений.

Тогда исходное неравенство равносильно совокупности систем:

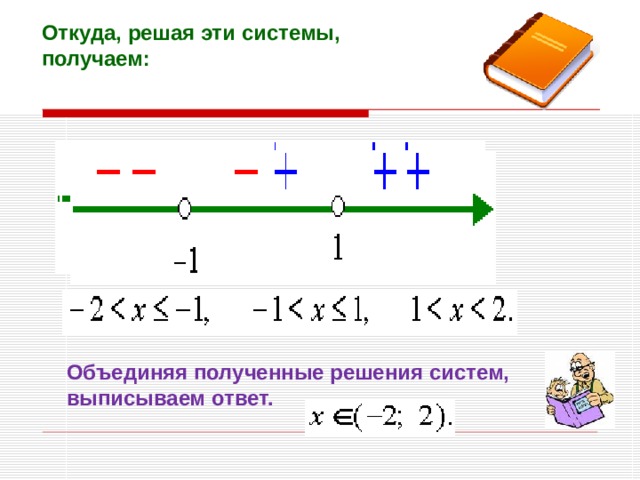
Откуда, решая эти системы, получаем:

Объединяя полученные решения систем, выписываем ответ.

Выводы и предложения:

• Данная модель исследования способна решать обучающие задачи по теме «Метод интервалов»
• Данная тема настолько обширна, что возникает необходимость продолжать работу( например при изучении исследования функций на монотонность и экстремумы)

Выводы и предложения:

• Использовать систематизированный материал как учбное пособие при подготовке к ЕГЭ.
• Предлагаемые домашние задания по пройденным разделам:

Задачи для самостоятельного решения

Решить неравенства

Ответы

ЖЕЛАЕМ УСПЕХА!

Литература

• Агафонов Б.Г.Повторим математику. Издательство «Высшая школа» М.1968 г.
• Агалаков С.А. Математика Е.Г.Э.(часть «С».Омск-2004.
• Дорофеев Г.В. , М.К.Потапов. Пособие по математике «Нестандартные задачи». Издательство «Наука» М.1976 г.
• Далингер В.А. Нестандартные уравнения , неравенства и методы их решения.Омск-1995 г.
• Моденов В. П. Пособие для поступающих в вузы. Издательство «Наука» 1984 г.
• Шарыгин И.Ф. Факультативный курс по математике

М. «Просвещение» 1991 г.