
Элективный курс по теме:
МЕТОД МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ В ЭКОНОМИКЕ
Автор:
Агжитова Наталья Владимировна ,
учитель математики МОУ СОШ № 31 города Тамбова.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Цели элективного курса:
- показать применение математических моделей при решении задач экономического характера,
- профильная и предпрофильная подготовка учащихся,
- систематизация ЗУН при решении текстовых задач,
- расширение кругозора учащихся.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Проблема:
Каким образом современная математика применяется к изучению физических, астрономических, биологических, экономических, гуманитарных и других явлений?
Ответ:
С помощью построения и анализа математических моделей изучаемого явления.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Что же такое математическая модель?
Определение:
Математическая модель - приближенное описание какого-либо явления внешнего мира, выраженное с помощью математической символики и заменяющее изучение этого явления исследованием и решением математических задач.
© Тамбов, МОУ СОШ № 31, 2008

Уточнение модели
Метод математических моделей в экономике
Что называется математическим моделированием?
Изучение явлений с помощью математических моделей называется математическим моделированием .
Схематический процесс математического моделирования:
Явление внешнего мира.
Его приближенное описание. Запись основных свойств и
соотношений между ними на математическом языке,
формулировка основных математических задач.
Решение математических задач, исследование решений.
Выводы. Новые свойства изучаемого явления, прогнозы,
сравнение с известными результатами.
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
Урбен Жан Жозеф Леверье
(1811 – 1877)
Работы Леверье посвящены решению проблем небесной механики. Открытие Нептуна с помощью предвычислений Леверье - одно из крупнейших событий в области теоретической астрономии.
Теория планет Леверье использовалась для составления астрономических эфемерид - таблиц положений тел Солнечной системы.
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
Джеймс Клерк Максвелл
(1831 – 1879)
Английский физик, создатель классической электродинамики, один из основоположников статистической физики, основатель одного из крупнейших мировых научных центров.
Создал теорию электромагнитного поля, предсказал существование электромагнитных волн, выдвинул идею электромагнитной природы света, установил первый статистический закон - закон распределения молекул по скоростям, названный его именем.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Фридман Александр Александрович
(1888 – 1925)
Математик и геофизик, создатель теории нестационарной Вселенной.
Основные труды по гидродинамике, динамической метеорологии, теоретической физике и др. Предложил модель нестационарной Вселенной, которая легла в основу современной космологии.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Задача № 1
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Пусть
x – количество прогулочных велосипедов, выпускаемых ежемесячно фирмой
y – количество спортивных велосипедов, выпускаемых ежемесячно фирмой.
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
0 ≤ x ≤ 600
0 ≤ y ≤ 300
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Занятость стенда А составляет 0,3 x + 0,4 y ( ч ), что не должно превышать 240 ч . Поэтому 0,3 x + 0,4 y ≤ 240 .
Аналогично для стенда В имеем 0,1 x + 0,3 y ≤ 120 .
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В . Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч на стенде В , а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч на стенде В . По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В – более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 рублей , а каждого спортивного – 90 рублей . Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей?
Прибыль фирмы составляет S = 50 x + 90 y ( руб .)
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Математическая задача:
Найти целые значения x и y , удовлетворяющие системе неравенств:
0,3 x + 0,4 y ≤ 240,
0,1 x + 0,3 y ≤ 120,
0≤ x ≤600,
0≤ y ≤300;
и такие, что прибыль S = 50 x + 90 y была наибольшей.
© Тамбов, МОУ СОШ № 31, 2008
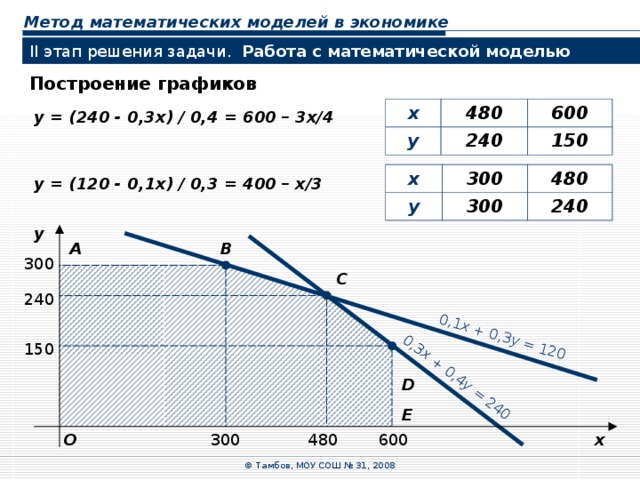
0,1 x + 0,3 y = 120
0,3 x + 0,4 y = 240
Метод математических моделей в экономике
II этап решения задачи. Работа с математической моделью
Построение графиков
x
y
480
240
600
150
y = ( 240 - 0,3 x) / 0,4 = 600 – 3x/4
x
300
y
480
300
240
y = (120 - 0, 1x) / 0, 3 = 400 – x/3
y
B
A
300
C
240
150
D
E
O
x
600
480
300
© Тамбов, МОУ СОШ № 31, 2008
0,1 x + 0,3 y = 120
0,3 x + 0,4 y = 240
Метод математических моделей в экономике
II этап решения задачи. Работа с математической моделью
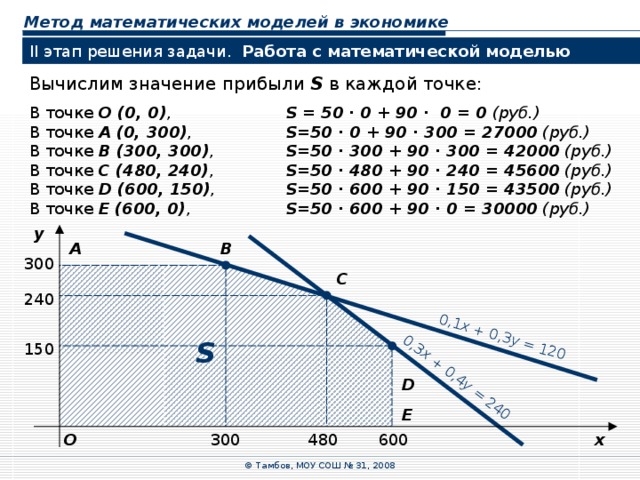
Вычислим значение прибыли S в каждой точке:
В точке O (0, 0) , S = 50 ∙ 0 + 90 ∙ 0 = 0 (руб.)
В точке A (0, 300) , S =50 ∙ 0 + 90 ∙ 300 = 27000 (руб.)
В точке B (300, 300) , S =50 ∙ 300 + 90 ∙ 300 = 42000 (руб.)
В точке C (480, 240) , S =50 ∙ 480 + 90 ∙ 240 = 45600 (руб.)
В точке D (600, 150) , S =50 ∙ 600 + 90 ∙ 150 = 43500 (руб.)
В точке E (600, 0) , S =50 ∙ 600 + 90 ∙ 0 = 30000 (руб.)
y
A
B
300
C
240
S
150
D
E
x
O
600
480
300
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
III этап. Анализ результатов
Наибольшее значение прибыли равно 45600 рублей
и достигается оно в точке C , т. е. при выпуске
480 прогулочных велосипедов и 240 – спортивных .
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Задача № 2
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
При простом процентном росте:
S n = (1 + p ∙ n / 100) ∙ S , где S n – сумма денег через n количества лет, S – первоначальная сумма, p – количество процентов за год, n – количество лет.
300 000 = (1 + 0,06) ∙ S 1
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
При простом процентном росте:
S n = (1 + p ∙ n / 100) ∙ S , где S n – сумма денег через n количества лет, S – первоначальная сумма, p – количество процентов за год, n – количество лет.
25 0 000 = (1 + 0,06) ∙ S 2
© Тамбов, МОУ СОШ № 31, 2008
Метод математических моделей в экономике
I этап решения задачи. Составление математической модели
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно , 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
Вы решили продать дом. Первый из двух имеющихся покупателей предлагает вам заплатить за дом 200000 рублей немедленно и еще 300000 рублей через 1 год . Второй покупатель предлагает вам за дом 100000 рублей немедленно, 250000 рублей через 1 год и еще 200000 рублей через 2 года . При условии, что ставка банков не меняется в течение 3 лет и составляет 6% годовых .
Какой из покупателей предлагает вам наилучшие условия?
При сложном процентном росте:
S n = (1 + p / 100) n ∙ S , где S n – сумма денег через n количества лет, S – первоначальная сумма, p – количество процентов за год, n – количество лет.
2 00 000 = (1 + 0,06) 2 ∙ S 3 ,
S 3 = 2 00 000 / (1 + 0,06) 2 = 177 999,28 руб.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
II этап решения задачи. Работа с математической моделью
Первый покупатель.
300 000 = (1 + 0,06) ∙ S 1
S 1 = 3 00 000 / (1 + 0,06) = 283 018, 86 руб.
200 000 + 283 018,86 = 483 018,86 руб.
Второй покупатель.
25 0 000 = (1 + 0,06) ∙ S 2
S 2 = 25 0 000 / (1 + 0,06) = 235 849, 05 руб.
2 00 000 = (1 + 0,06) 2 ∙ S 3 ,
S 3 = 2 00 000 / (1 + 0,06) 2 = 177 999,28 руб.
100 000 + 235 849,05 + 177 999,28 = 513 848,33 руб.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
III этап. Анализ результатов
Сравнив результаты вычислений, получаем, что второй покупатель предлагает вам за дом на 513 848,33 – 483 018,86 = 30 829,47 руб . больше, чем первый покупатель.
© Тамбов, МОУ СОШ № 31, 2008

Метод математических моделей в экономике
Вывод:
С помощью построения и анализа математических моделей различных явлений современная математика применяется к изучению физических, астрономических, биологических, экономических и других явлений.
© Тамбов, МОУ СОШ № 31, 2008


 Получите свидетельство
Получите свидетельство Вход
Вход




























 Метод математических моделей в экономике (2.24 MB)
Метод математических моделей в экономике (2.24 MB)
 0
0 903
903 98
98 Нравится
0
Нравится
0








