Метод координат

Данная работа может быть испльзована во время урока, а также является дополнительным материалом при подготовке к ЕГЭ.

Сведения из теории:

1.Вектор перпендикулярный  к плоскости называется  нормальным вектором.

2.Угол между плоскостями равен углу между нормальными  векторами этих плоскостей.

Весь материал - в документе.

Кеушкова Т.Б.

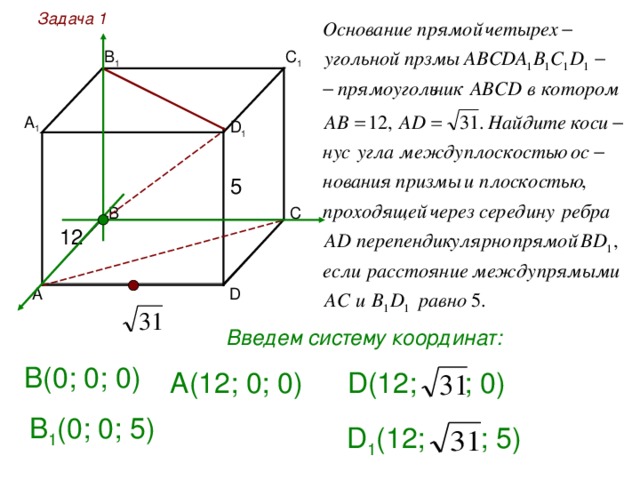
Задача 1

С 1

В 1

А 1

D 1

5

12

D

Введем систему координат:

В(0; 0; 0)

А(12; 0; 0)

D ( 12 ; ; 0)

В 1 (0; 0; 5 )

D 1 ( 12 ; ; 5 )

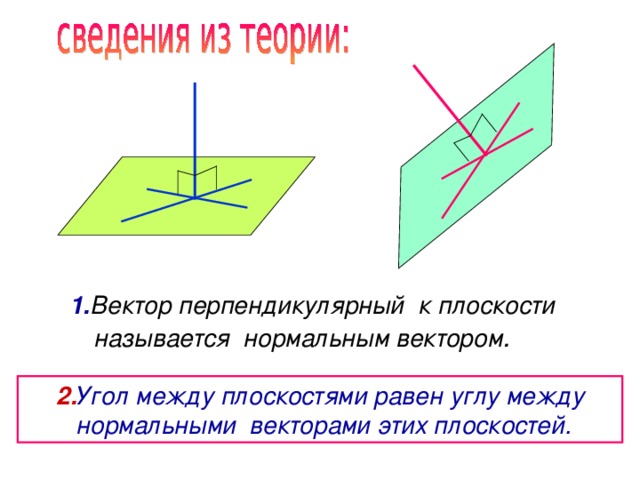
1. Вектор перпендикулярный к плоскости называется нормальным вектором .

2. Угол между плоскостями равен углу между

нормальными векторами этих плоскостей.

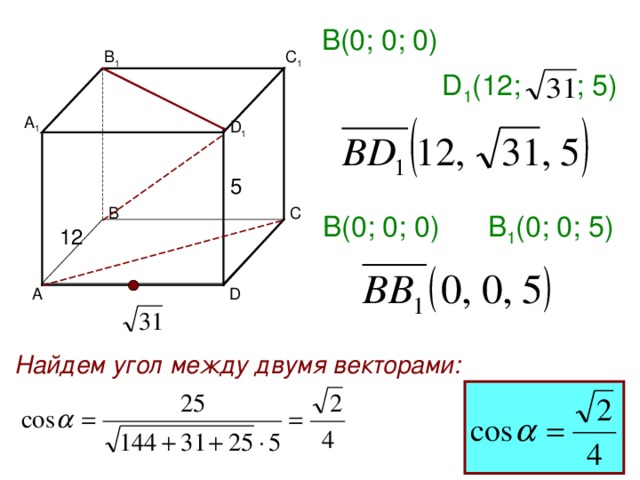
В(0; 0; 0)

В 1

С 1

D 1 ( 12 ; ; 5 )

А 1

D 1

5

В 1 (0; 0; 5 )

В(0; 0; 0)

12

D

Найдем угол между двумя векторами:

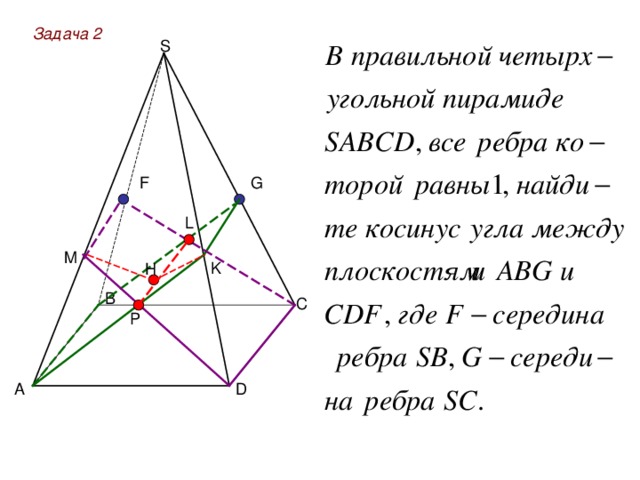
Задача 2

S

G

F

L

M

K

H

P

D

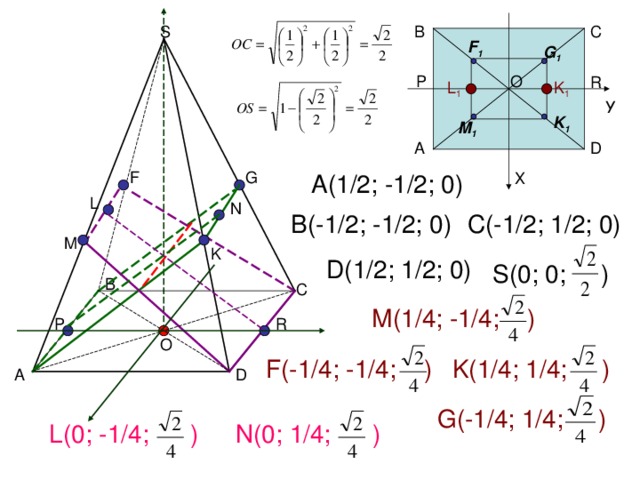
S

F 1

G 1

P

O

R

K 1

L 1

K 1

М 1

D

F

G

А(1 /2 ; -1/2; 0)

L

N

B ( - 1 /2 ; -1/2; 0)

C ( - 1 /2 ; 1/2; 0)

M

K

D (1 /2 ; 1/2; 0)

S ( 0 ; 0 ; )

М(1 / 4; -1/4; )

P

R

O

F (-1 / 4; -1/4; )

K (1 / 4; 1/4; )

D

G ( - 1 / 4; 1/4; )

L ( 0 ; -1/4; )

N ( 0 ; 1/4; )

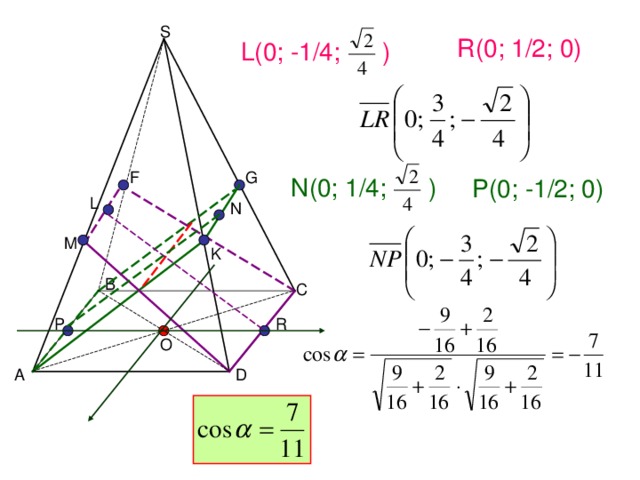
S

L ( 0 ; -1/4; )

R ( 0 ; 1 /2; 0)

G

F

N ( 0 ; 1/4; )

P ( 0 ; -1 /2; 0)

L

N

M

K

R

P

O

D

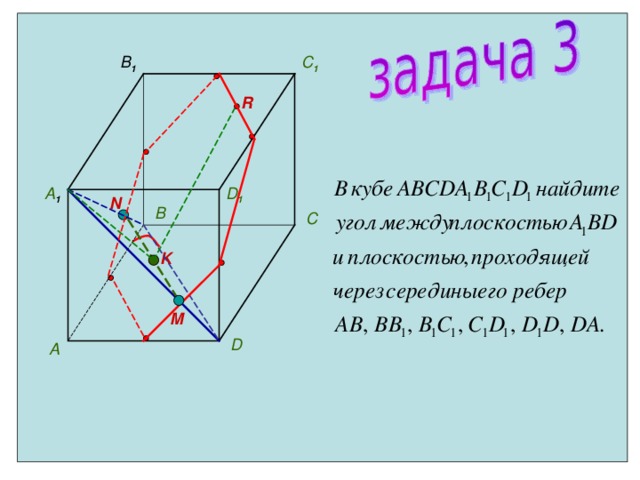
C 1

B 1

R

D 1

А 1

N

В

С

K

M

D

А

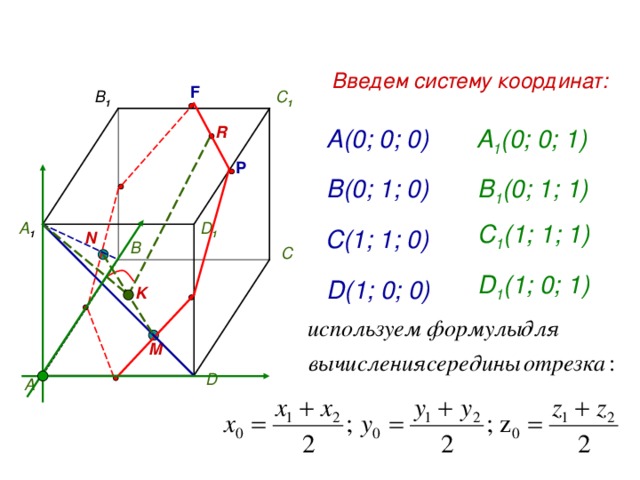
Введем систему координат:

F

B 1

C 1

R

А(0; 0; 0)

А 1 (0; 0; 1 )

Р

B 1 (0; 1 ; 1 )

В(0; 1; 0)

D 1

А 1

C 1 ( 1 ; 1 ; 1 )

С(1; 1; 0)

N

В

С

D 1 ( 1 ; 0; 1 )

D ( 1 ; 0; 0)

K

D

M

D

А

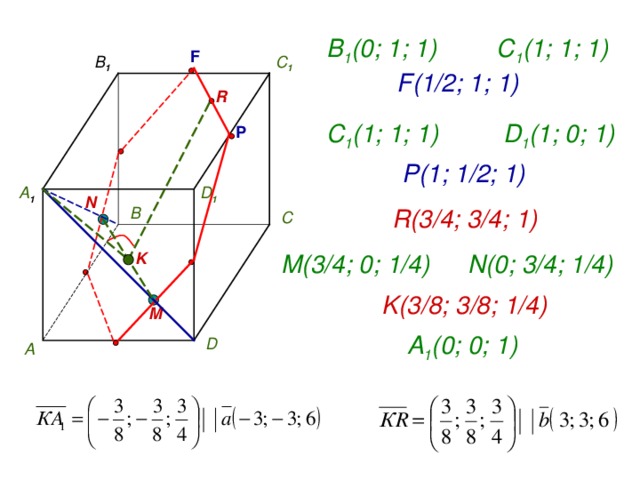
C 1 ( 1 ; 1 ; 1 )

B 1 (0; 1 ; 1 )

F

B 1

C 1

F ( 1/2 ; 1 ; 1 )

R

D 1 ( 1 ; 0; 1 )

C 1 ( 1 ; 1 ; 1 )

Р

P ( 1 ; 1/2 ; 1 )

А 1

D 1

N

В

R ( 3/4 ; 3/4 ; 1 )

С

K

M ( 3/4 ; 0 ; 1/4 )

N ( 0 ; 3/4 ; 1/4 )

K ( 3/8 ; 3/8 ; 1/4 )

M

А 1 (0; 0; 1 )

D

А

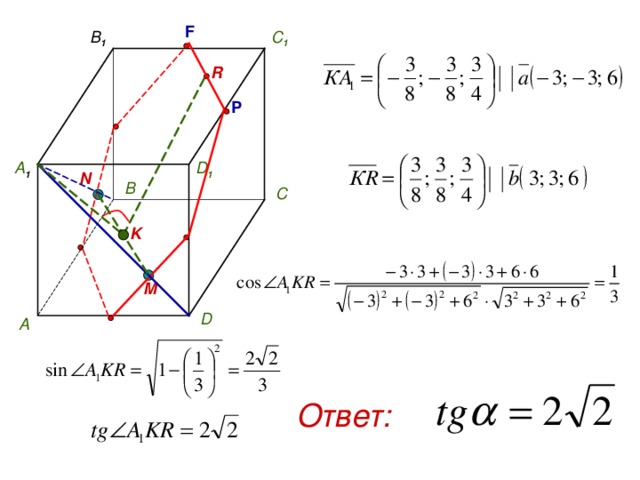
F

B 1

C 1

R

Р

D 1

А 1

N

В

С

K

M

D

А

Ответ:

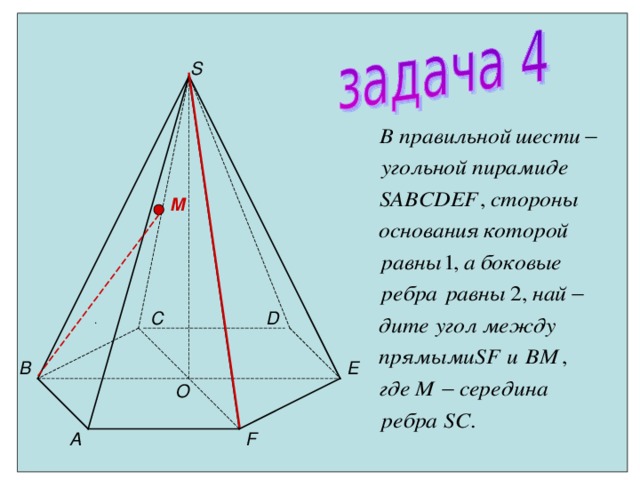
S

M

D

С

.

E

В

O

F

А

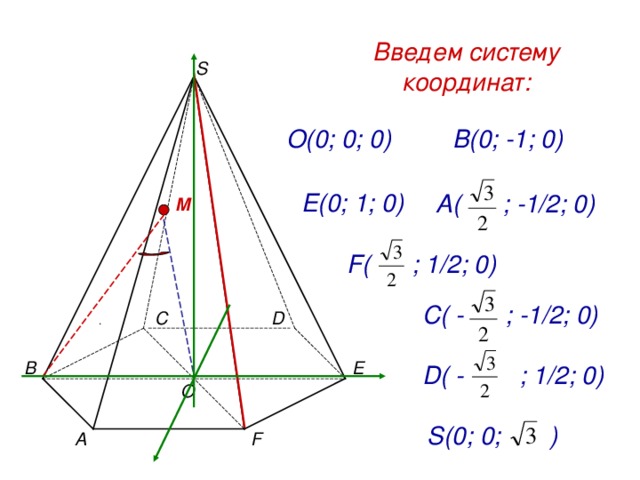
Введем систему

координат:

S

В(0; -1; 0)

О(0; 0; 0)

Е(0; 1; 0)

А( ; -1/2; 0)

M

F ( ; 1/2 ; 0)

C ( - ; -1/2; 0)

С

D

.

E

В

D ( - ; 1/2 ; 0)

O

S (0; 0 ; )

F

А

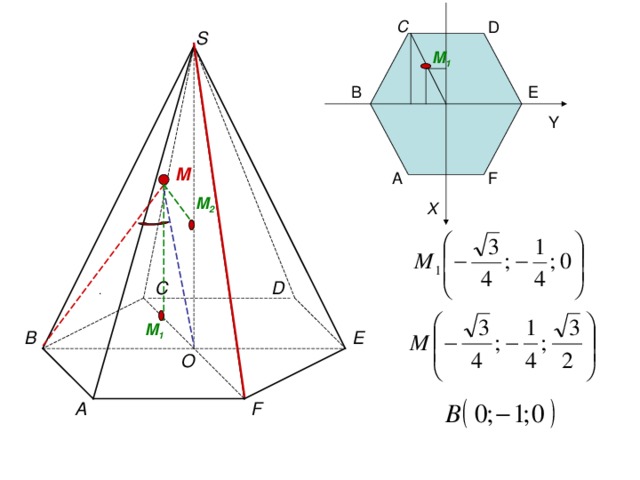
C

D

S

M 1

E

B

Y

M

A

F

M 2

X

D

С

.

M 1

E

В

O

F

А

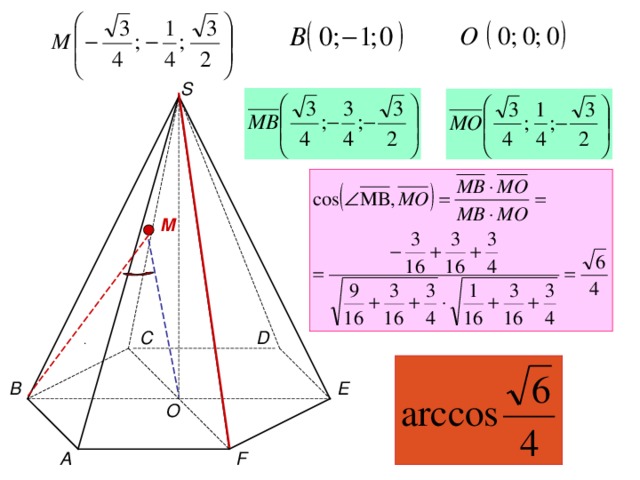
S

M

D

С

.

E

В

O

F

А

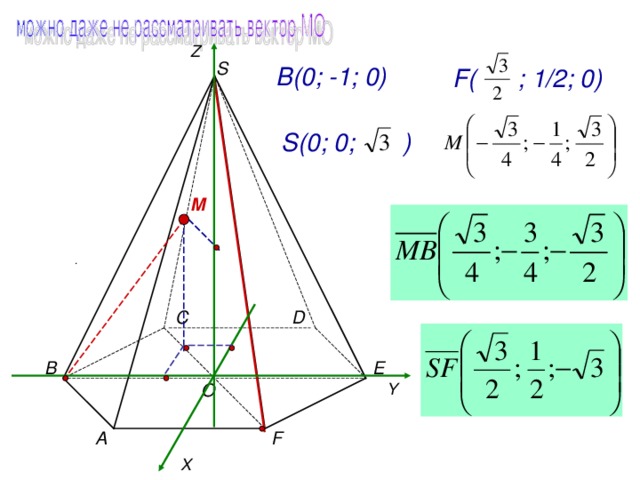
Z

S

В(0; -1; 0)

F ( ; 1/2 ; 0)

S (0; 0 ; )

M

.

С

D

В

E

O

Y

А

F

X

E 1

D 1

F 1

C 1

B 1

А 1

E

D

С

F

А

В

D

E

F

Y

O

E 1

D 1

X

F 1

C 1

А 1

B 1

D

E

F

С

А

В

E 1

D 1

F 1

C 1

А 1

B 1

D

E

F

С

А

В

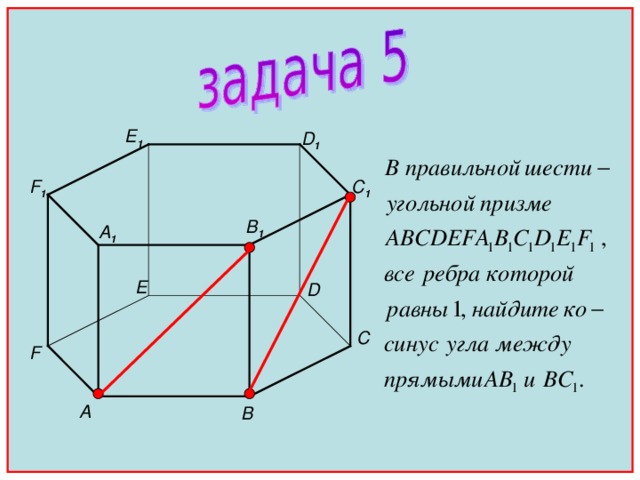
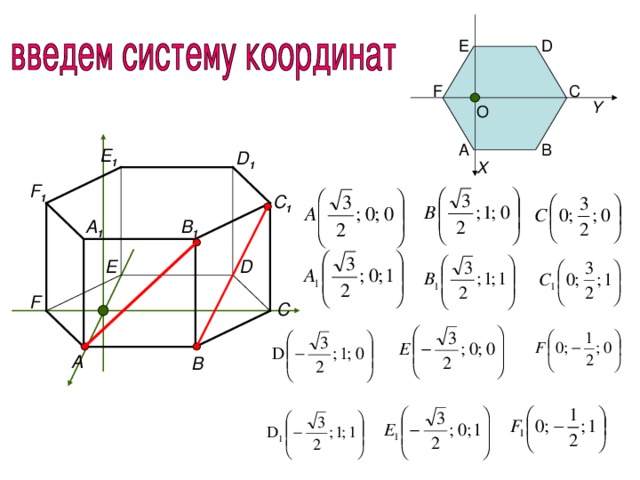
Задача 6

F

В 1

С 1

6

6

А 1

D 1

4

E

Введем систему координат:

D

В(0; 0; 0)



E ( 3 ; 0; 0)

F (0; 3 ; 4 )



A ( 6 ; 0 ; 0 )

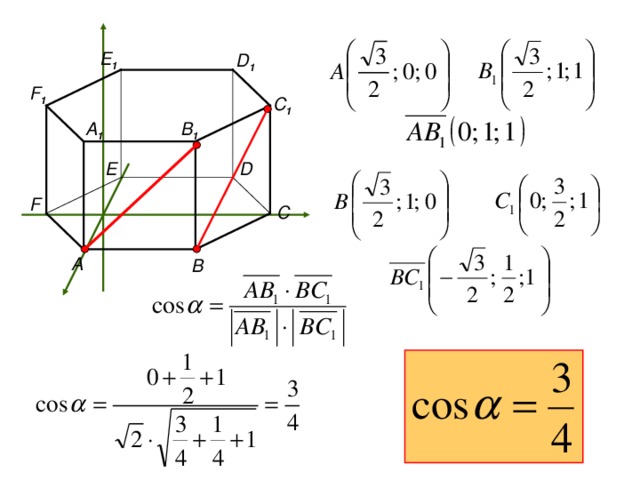
F

E ( 3 ; 0; 0)

F (0; 3 ; 4 )

В 1

С 1

6

6

А 1

D 1

В(0; 0; 0)

A ( 6 ; 0 ; 0 )

5

4

E

D

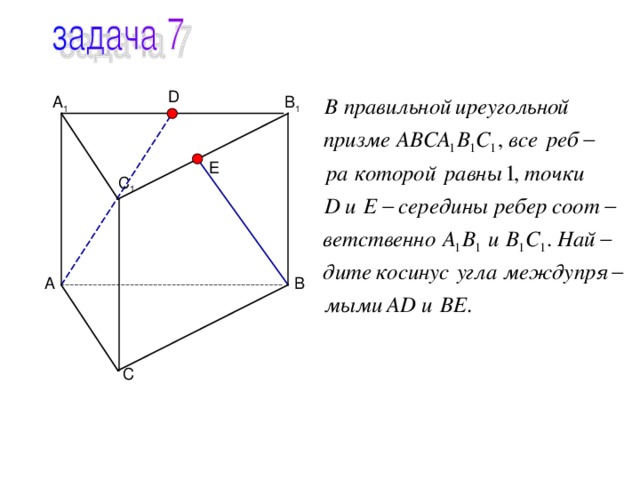
D

1

1

E

1

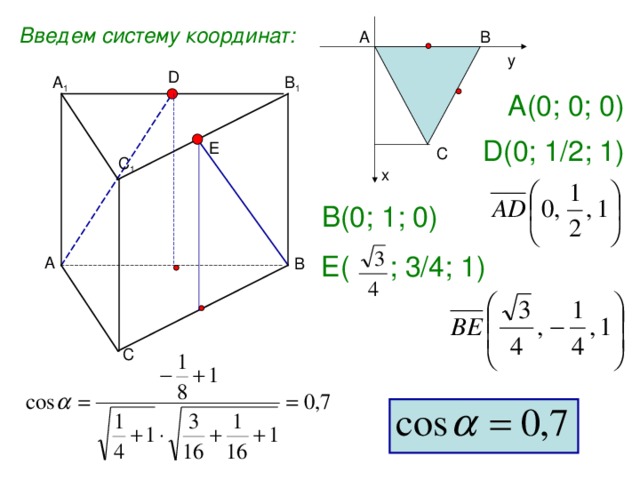
Введем систему координат:

y

D

1

1

А(0; 0; 0)

D (0; 1/2 ; 1 )

E

1

x

В(0; 1; 0)

E ( ; 3/4 ; 1 )

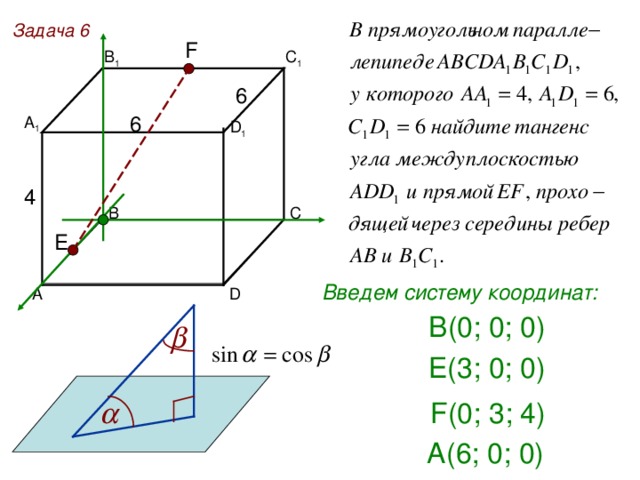
Задача 8

С 1

В 1

D 1

А 1

H

В

С

А

D

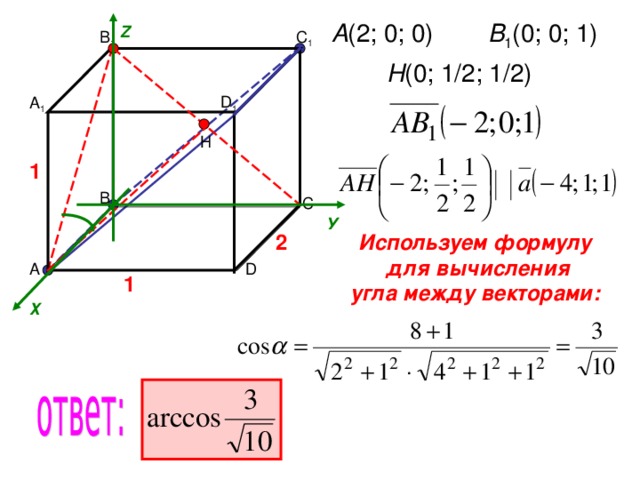
A (2 ; 0; 0)

В 1 ( 0; 0; 1)

Z

С 1

В 1

Н ( 0; 1/2; 1/2)

D 1

А 1

H

1

В

С

У

Используем формулу

для вычисления

угла между векторами:

2

А

D

1

Х

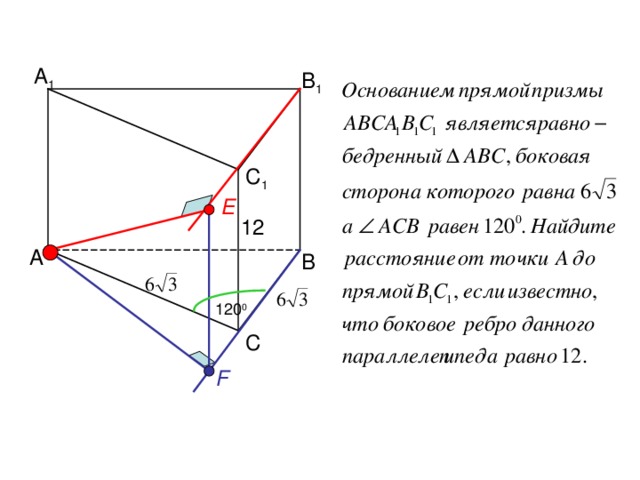
А 1

В 1

С 1

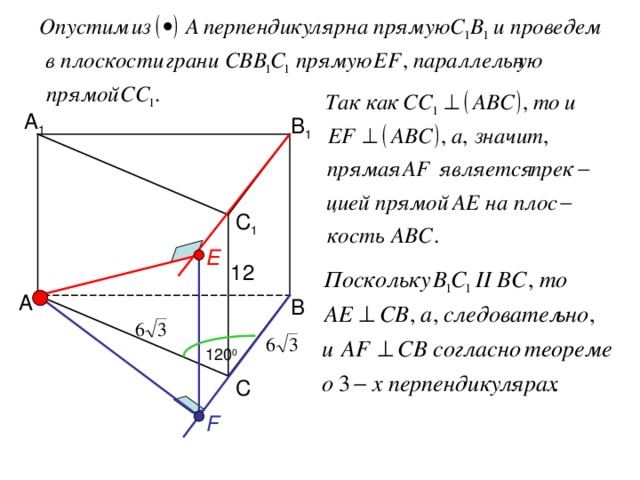
E

12

А

В

120 0

С

F

А 1

В 1

С 1

E

12

А

В

120 0

С

F

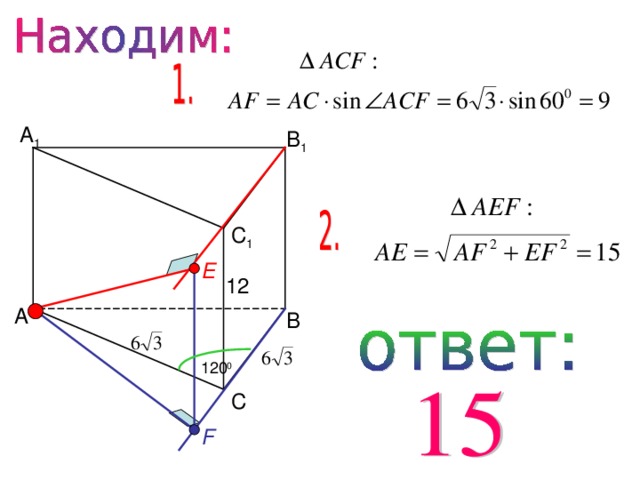
А 1

В 1

С 1

E

12

А

В

120 0

С

F

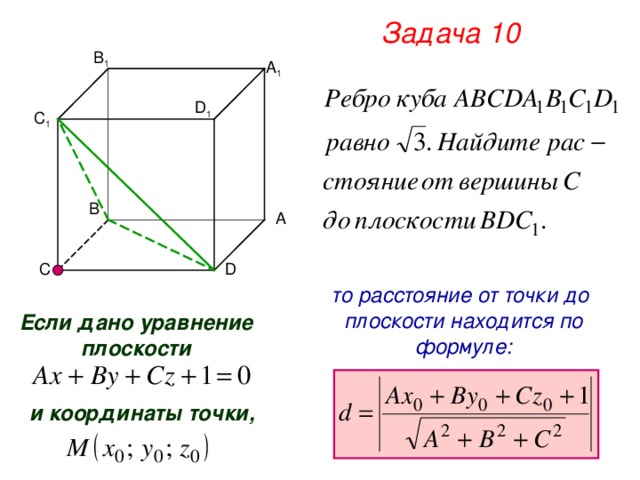
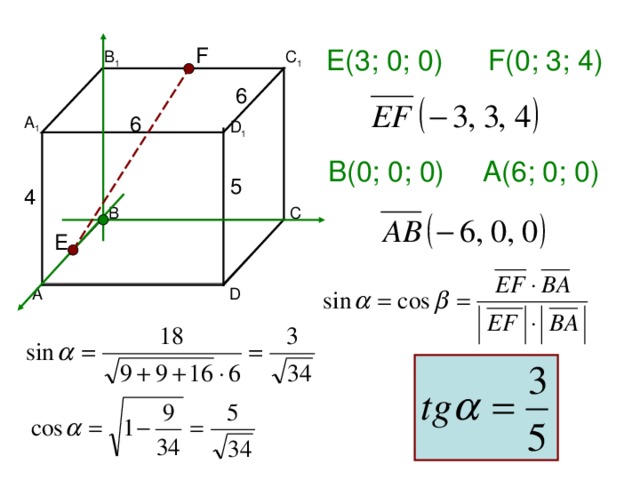
Задача 10

В 1

А 1

D 1

С 1

В

А

С

D

то расстояние от точки до

плоскости находится по

формуле:

Если дано уравнение

плоскости

и координаты точки,

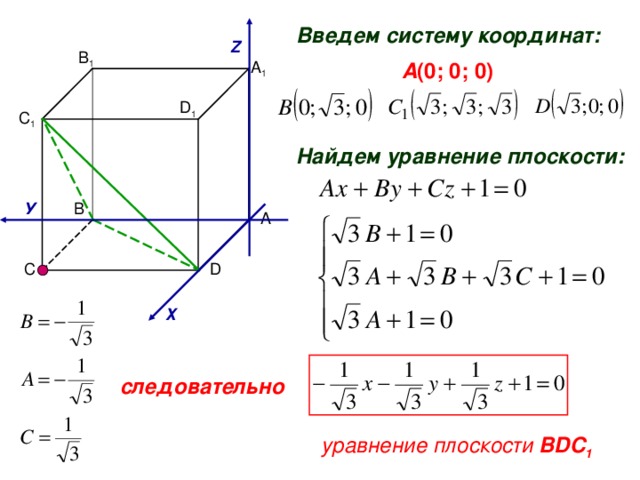
Введем систему координат:

Z

В 1

A (0 ; 0; 0)

А 1

D 1

С 1

Найдем уравнение плоскости:

В

У

А

С

D

Х

следовательно

уравнение плоскости BDC 1

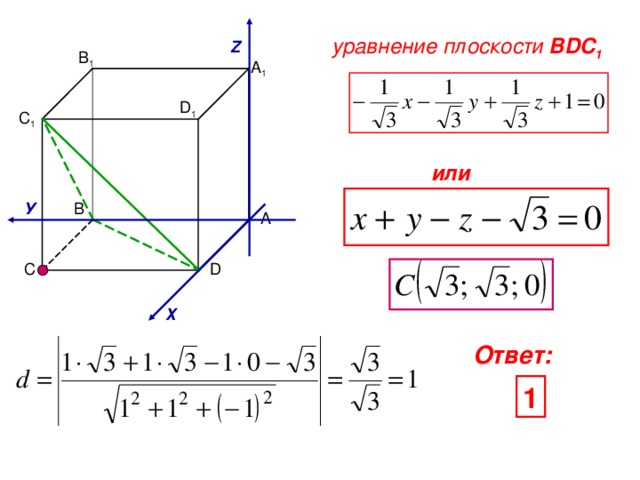
уравнение плоскости BDC 1

Z

В 1

А 1

D 1

С 1

или

У

В

А

С

D

Х

Ответ:

1

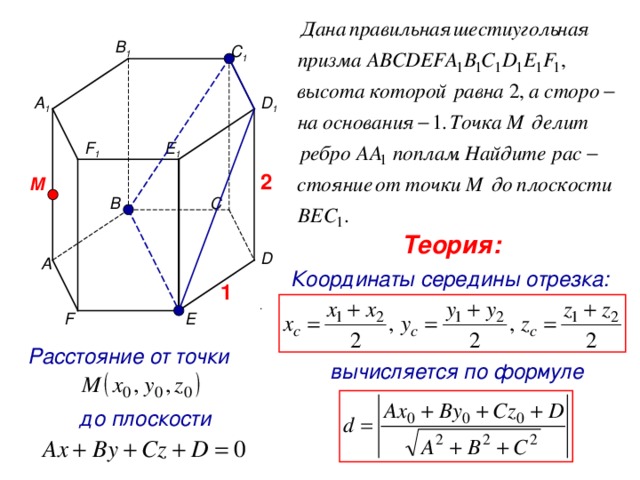
В 1

С 1

А 1

D 1

E 1

F 1

2

M

С

В

Теория:

D

А

Координаты середины отрезка:

1

.

E

F

Расстояние от точки

вычисляется по формуле

до плоскости

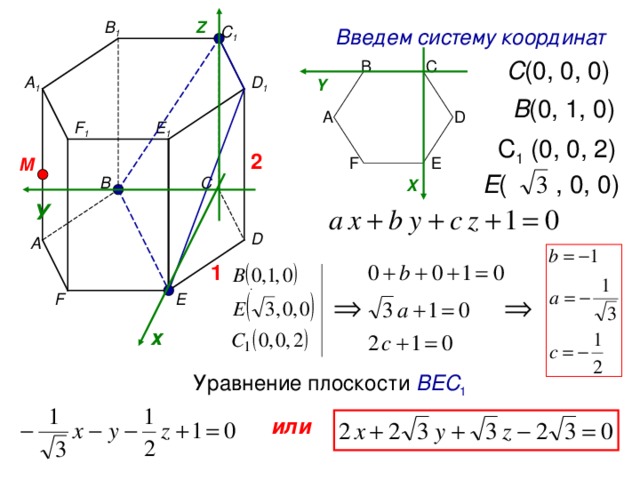
Z

В 1

С 1

Введем систему координат

C (0, 0, 0)

C

B

D 1

А 1

Y

B (0, 1, 0)

A

D

F 1

E 1

C 1 (0, 0, 2)

2

F

E

M

E ( , 0, 0)

С

В

X

У

D

А

1

.

E

F

х

Уравнение плоскости ВЕС 1

или

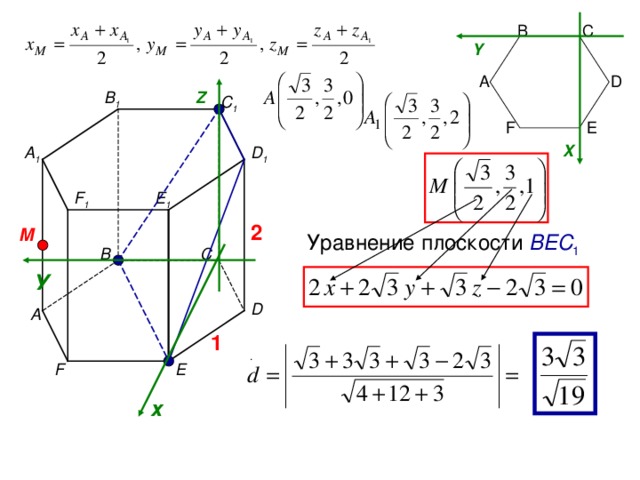
B

C

Y

A

D

В 1

Z

С 1

E

F

X

D 1

А 1

E 1

F 1

2

M

Уравнение плоскости ВЕС 1

С

В

У

D

А

1

.

E

F

х