Механические колебания

1. Колебания

Не так легко дать полное определение понятию “колебания”.  Не даром Л. И. Мандельштам в своих лекциях сказал: “Резко разграничить, что такое колебания, а что не колебания также трудно, как определить, что такое лысый человек или что такое куча”.

КОЛЕБАНИЯ - это одномерное движение какого-либо тела около положения устойчивого равновесия.

Наименьшее время, через которое оно повторяется называют периодом.

Таким образом, движения “туда–обратно” и периодичность – это лишь некоторые признаки колебаний.

Не каждое колебательное движение периодично и не всякое периодическое движение является колебаниями.

Например, любое равномерное вращение тела является периодическим движением, так как при каждом обороте всякая точка равномерно вращающегося тела проходит те же положения, что и при предыдущем обороте, причем в такой же последовательности и с теми же скоростями. Период такого равномерного вращения равен продолжительности одного оборота.

Рассмотрим примеры:

1. Пусть на крышке стола тело массой m равномерно вращается по окружности.

Если мы посмотрим сверху, то увидим, что движение происходит по окружности. А вот человек, который смотрит “в торец” стола и видит проекцию кругового движения на ось х, может подумать, что наблюдает  колебательное движение туда и обратно.

2. Натянутую струну выведем из равновесия в поперечном направлении - струна совершает колебания.

3. Отклоним конусный сосуд заполненный песком – теперь он тоже совершает колебания.

Колебания бывают как периодическими, так и непериодическими. Если возврат к положению равновесия совершается через равные промежутки времени, то такие колебания называются периодическими. Непериодические колебания гораздо разнообразнее периодических.

Нужно рассматривать состояние не в данный момент, а процесс в целом за определенное время.

2. Свободные колебания

Колеблющееся тело всегда связано с другими телами и вместе с ними образует колебательную систему.

Если колебательная система не подвергается переменным внешним воздействиям, то колебания, возникающие вследствие какого-либо отклонения этой системы от состояния устойчивого равновесия, называют свободными (собственными).

Свободные колебания в идеальных колебательных системах называются гармоническими. Они являются специальным, частным видом периодического колебания.

Для того чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело (возвращающая сила) в положение равновесия, была пропорциональна смещению тела из положения равновесия. Этому условию для случая пружины удовлетворяет сила Гука.

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛУГАНСКОЙ ОБЛАСТНОЙ ГОСУДАРСТВЕННОЙ АДМИНИСТРАЦИИ

КУ "ЛУГАНСКАЯ ОБЛАСТНАЯ МАЛАЯ АКАДЕМИЯ НАУК УЧАЩЕЙСЯ МОЛОДЕЖИ"

автор – составитель : А. С. Воронкин

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Луганск - 201 3

ТЕМА 2.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

План

2. 1. Колебания

2 . 2. Свободные колебания

2.3. Гармоническое колебание. Гармонические осцилляторы

2.4. Графическое представление гармонического колебания

2.5. Математический маятник

2.6. Пружинный маятник

2.7. Дифференциальное уравнение гармонических колебаний

2.8. Энергия гармонического колебания

2.9. Вынужденные колебания и резонанс

2.10. Автоколебания

2.11. Классификация колебаний

2 . 1. Колебания

• Не так легко дать полное определение понятию “ колебания ” . Не даром Л. И. Мандельштам в своих лекциях сказал : “ Резко разграничить, что такое колебания, а что не колебания также трудно, как определить, что такое лысый человек или что такое куча ” .

Мандельштам Л. И. является одним из создателей нелинейной теории колебаний, творцом радиоинтерференционных методов определения скорости распространения радиоволн.

Совместно с Г. С. Ландсбергом изучал комбинационное рассеяние света на кристаллах.

Леонид Исаакович Мандельштам

(1879-1944)

• КОЛЕБАНИЯ - это одномерное движение какого-либо тела около положения устойчивого равновесия .

• Наименьшее время, через которое оно повторяется называют периодом .
• Таким образом, движения “ туда–обратно ” и периодичность – это лишь некоторые признаки колебаний .

• Не каждое колебательное движение периодично и не всякое периодическое движение является колебаниями.

Например, любое равномерное вращение тела является периодическим движением, так как при каждом обороте всякая точка равномерно вращающегося тела проходит те же положения, что и при предыдущем обороте, причем в такой же последовательности и с теми же скоростями . Период такого равномерного вращения равен продолжительности одного оборота.

Р А С С М О Т Р И М П Р И М Е Р Ы

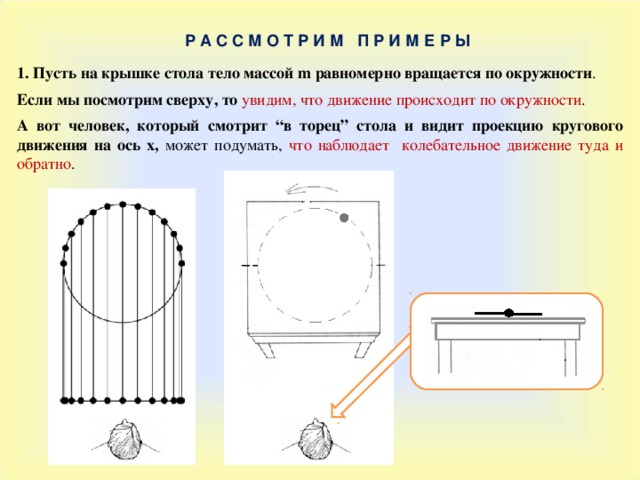
1. Пусть на крышке стола тело массой m равномерно вращается по окружности .

Если мы посмотрим сверху, то увидим, что движение происходит по окружности .

А вот человек, который смотрит “ в торец ” стола и видит проекцию кругового движения на ось х, может подумать, что наблюдает колебательное движение туда и обратно .

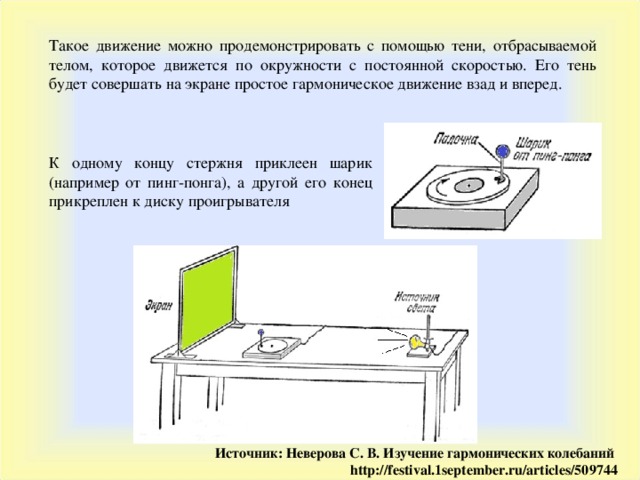
Такое движение можно продемонстрировать с помощью тени, отбрасываемой телом, которое движется по окружности с постоянной скоростью. Его тень будет совершать на экране простое гармоническое движение взад и вперед.

К одному концу стержня приклеен шарик ( например от пинг-понга), а другой его конец прикреплен к диску проигрывателя

Источник : Неверова С. В. Изучение гармонических колебаний

http://festival.1september.ru/articles/509744

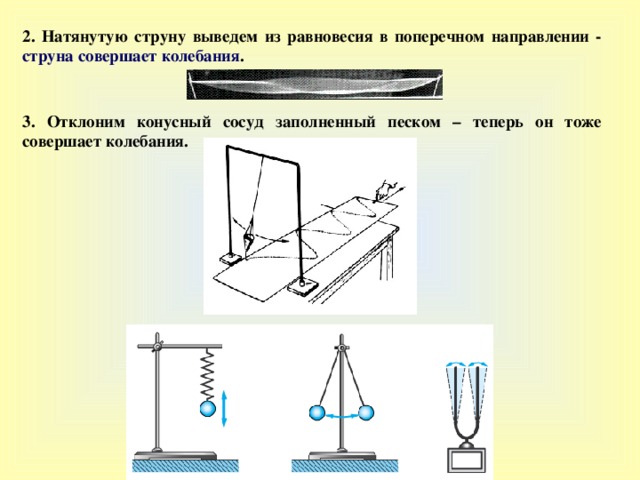
2. Н атянутую струну выведем из равновесия в поперечном направлении - струна совершает колебания .

3. Отклоним конусный сосуд заполненный песком – теперь он тоже совершает колебания.

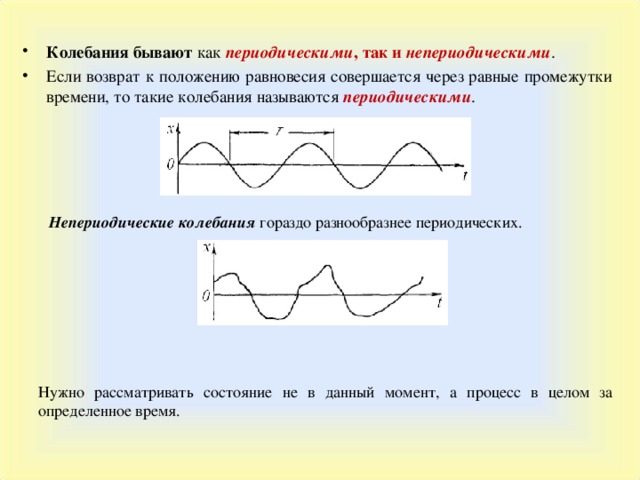
• Колебания бывают как периодическими , так и непериодическими .
• Если возврат к положению равновесия совершается через равные промежутки времени, то такие колебания называются периодическими .

Непериодические колебания гораздо разнообразнее периодических.

Нужно рассматривать состояние не в данный момент, а процесс в целом за определенное время.

2 .2 . Свободные колебания

Колеблющееся тело всегда связано с другими телами и вместе с ними образует колебательную систему .

Если колебательная система не подвергается переменным внешним воздействиям, то колебания, возникающие вследствие какого-либо отклонения этой системы от состояния устойчивого равновесия, называют свободными ( собственными) .

колебания груза

на пружине

Свободные колебания с течением времени всегда затухают .

Свободные колебания в идеальных колебательных системах называются гармоническими . Они являются специальным, частным видом периодического колебания .

Для того чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело (возвращающая сила) в положение равновесия, была пропорциональна смещению тела из положения равновесия .

Этому условию для случая пружины удовлетворяет сила Гука :

F – сила упругости (или упругая сила), [ H ]

k – жесткость пружины. Зависит от формы, размеров и материала , [Н/м] .

∆ х – абсолютное удлинение или сжатие пружины, [м]

Знак минус показывает , что сила всегда направлена в сторону положения равновесия .

• Роберт Гук – английский физик, математик, учёный и изобретатель.
• В 1662 г. получил степень магистра искусств.
• В 1678 г. опубликовал работу " De potentia restitutiva or of spring " ( О б упругости ). В ней содержатся результаты проведенных Гуком опытов с упругими телами. Это был первый печатный труд, в котором рассматривались упругие свойства материалов.
• К концу жизни Р. Гук сделал около 500 научных и технических открытий

Роберт Гук

(1635-1703)

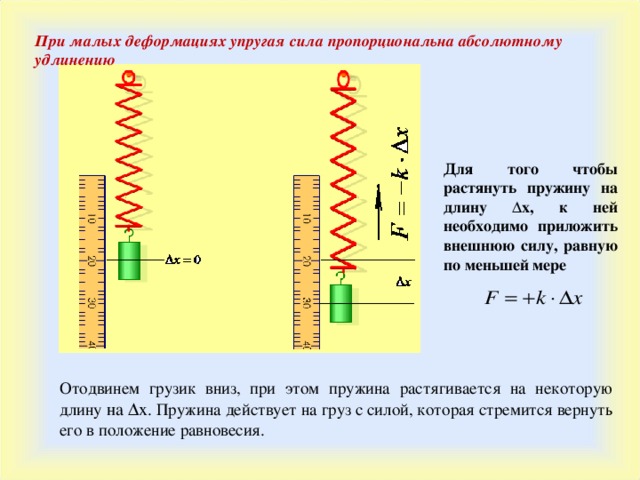
При малых деформациях упругая сила пропорциональна абсолютному удлинению

Для того чтобы растянуть пружину на длину ∆х, к ней необходимо приложить внешнюю силу, равную по меньшей мере

Отодвинем грузик вниз, при этом пружина растягивается на некоторую длину на ∆х . Пружина действует на груз с силой, которая стремится вернуть его в положение равновесия.

На рисунке, изображена доска, лежащая на двух подставках. Если на ее середину поместить гирю, то под действием силы тяжести гиря начнет двигаться, но через некоторое время, прогнув доску, остановится. При этом сила тяжести окажется уравновешенной силой Гука

Сила упругости возникает при деформации.

Деформация - это изменение формы или размеров тела.

Экспериментальное подтверждение Закона Гука на винтовой пружине при помощи набора гирек

В этом случае на пружину действует сила тяжести гирьки :

F = P=mg ,

m – маса гирьки,

g – ускорение свободного падения .

По 3-му закону Ньютона сила тяжести равна возвращающей силе пружины :

F упр= k∙∆x=mg=F

Пропорциональность между возвращающими силами, пока они достаточно малы,

и удлинением твердого тела наблюдается не только у пружин, но и у многих

материалов, находящихся в состоянии устойчивого равновесия

Коэффициент упругости (жесткость) для данной пружины k= F упр /∆x , [ Н / м ]

2 . 3. Гармоническое колебание. Гармонические осцилляторы

• Гармоническое колебание – это колебательный процесс, при котором периодические изменения физических величин, характеризующих состояние системы в зависимости от времени, происходят по закону синуса или косинуса .

• Уравнение гармонических колебаний имеет вид :

или

– это текущая фаза колебаний.

Фаза колебаний линейно растет со временем

– начальная фаза колебаний, т.е. фаза колебаний в начальный момент временит – при t=0

– амплитуда колебаний, т.е. максимальное отклонение колеблющейся величины от положения равновесия,

– циклическая частота, [ рад / с ]

Циклическую (круговую, угловую) частоту следует различать с линейной частотой ( f) .

Линейная частота определяет количество совершенных колебаний тела за единицу времени.

Если за время t совершено n колебаний, то f=n/t .

Измеряется частота в герцах [Гц] – единицах названных именем великого немецкого ученого Генриха Рудольфа Герца .

1 герц – это 1 полное колебание в секунду :

Единица измерения – Герц как мера количества повторяющихся событий в единицу времени была принята Международным бюро мер и весов в 1964 году как единица частоты в системе СИ.

В ноябре 1877 Генрих Герц в письме родителям написал: “ Раньше я часто говорил себе, что быть посредственным инженером для меня предпочтительней, чем посредственным ученым.

Но теперь я думаю, что прав Шиллер , сказавший: « кто трусит жизнью рисковать, тому успеха в ней не знать », и что излишняя осторожность была бы с моей стороны безумием ” .

Генрих Рудольф Герц

(1857-1894)

Время, за которое происходит одно полное колебание , называется периодом колебания :

[ c ]

где ω – циклическая частота.

Циклическая частота колебаний равна числу полных колебаний за 2 π секунд, т.е. ω =2 π f . Единица циклической частоты – [рад/c].

Д О П О Л Н Е Н И Е Единицы измерения плоских углов

• Плоский угол определяется отношением длины дуги к радиусу.

• 1 градус определяется как

• Радиан (рад) – это центральный угол, соответствующий дуге, длина которой равна ее радиусу :

Значение 360 градусов соответствует значению 2π радиан.

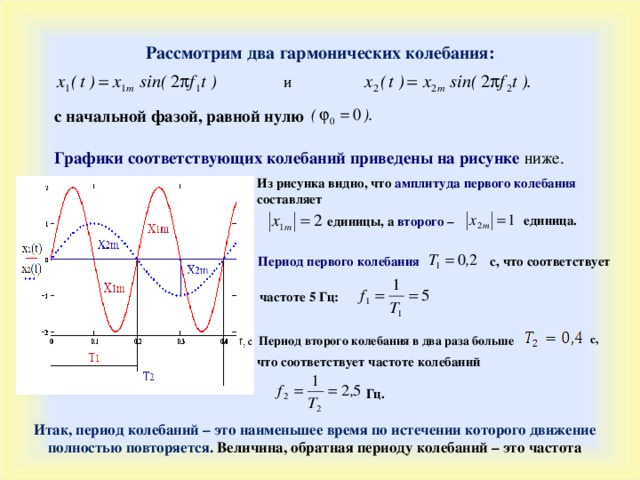
Рассмотрим два гармонических колебания :

и

с начальной фазой, равной нулю

Графики соответствующих колебаний приведены на рисунке ниже.

Из рисунка видно, что амплитуда первого колебания составляет

единица.

единицы, а второго –

Период первого колебания

с, что соответствует

частоте 5 Гц :

с,

Период второго колебания в два раза больше

что соответствует частоте колебаний

Гц.

Итак, период колебаний – это наименьшее время по истечении которого движение полностью повторяется . Величина, обратная периоду колебаний – это частота

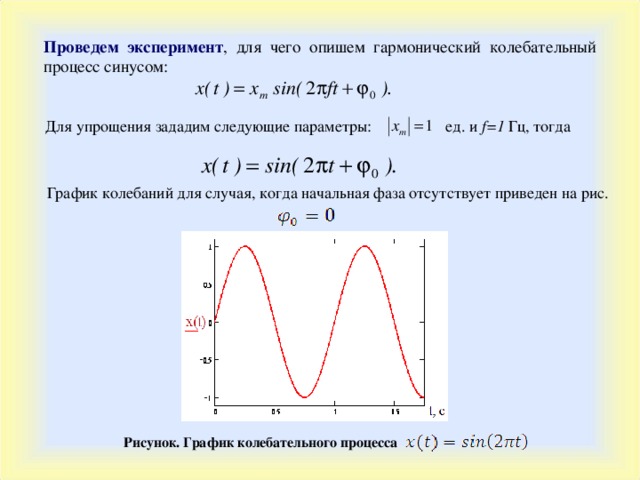
Проведем эксперимент , для чего опишем гармонический колебательный процесс синусом:

Для упрощения зададим следующие параметры:

ед. и f=1 Гц, тогда

График колебаний для случая, когда начальная фаза отсутствует приведен на рис.

Рисунок. График колебательного процесса

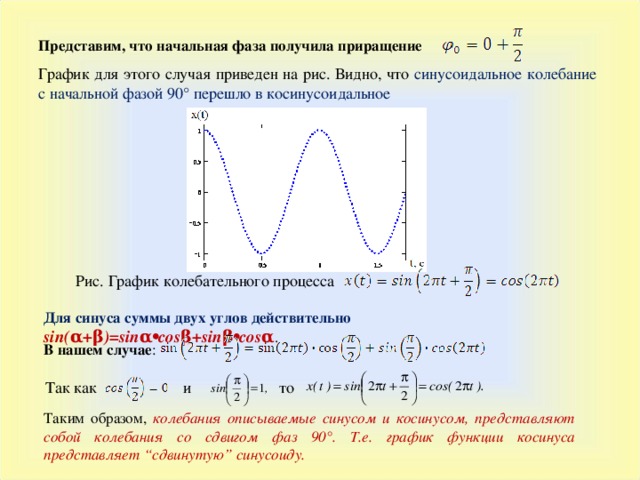
Представим, что начальная фаза получила приращение

График для этого случая приведен на рис. Видно, что синусоидальное колебание с начальной фазой 90° перешло в косинусоидальное

Рис. График колебательного процесса

Для синуса суммы двух углов действительно sin( α+β )=sin α •cos β +sin β •cos α .

В нашем случае :

то

Так как

и

Таким образом, колебания описываемые синусом и косинусом, представляют собой колебания со сдвигом фаз 90°. Т.е. график функции косинуса представляет “ сдвинутую ” синусоиду.

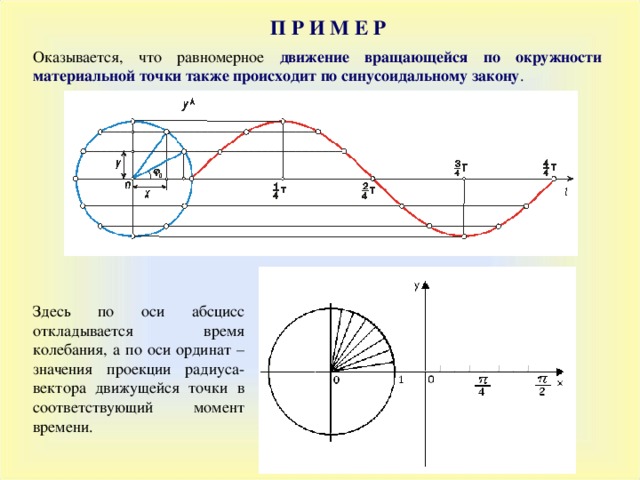
П Р И М Е Р

Оказывается, что равномерное движение вращающейся по окружности материальной точки также происходит по синусоидальному закону .

Здесь по оси абсцисс откладывается время колебания, а по оси ординат – значения проекции радиуса-вектора движущейся точки в соответствующий момент времени.

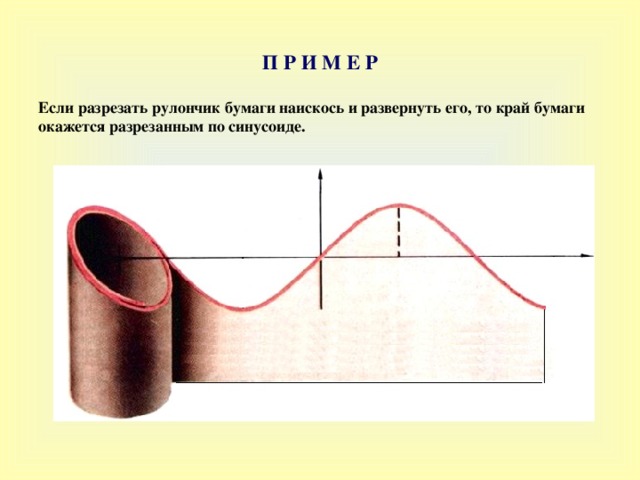
П Р И М Е Р

Если разрезать рулончик бумаги наискось и развернуть его, то край бумаги окажется разрезанным по синусоиде .

2 .2 . Графическое представление гармонического колебания

Графически гармонические колебания можно изображать используя метод вращающегося вектора амплитуды . Идея метода следующая. Из произвольной точки О на оси x под углом φ 0 (начальная фаза колебания) откладывается вектор

модуль которого равен амплитуде рассматриваемого колебания.

Приводя вектор Xm во вращение с угловой скоростью ω, равной циклической частоте колебания, получаем, что проекция конца вектора будет перемещаться по оси x и принимать значения от –Xm до + Xm, а колеблющаяся величина изменяться со временем по закону

2 . 5 . Математический маятник

Маятником является всякое тело, подвешенное так, что его центр тяжести находится ниже точки подвеса.

Математическим маятником называют колеблющуюся в гравитационном поле Земли материальную точку, подвешенную на невесомой и нерастяжимой нити длиной l .

Закон, по которому происходят колебания математического маятника, установил Галилео Галилей в 1583 г., наблюдая за качающимся подсвечником на длинной цепи в соборе в Пизе.

Оказалось, что период колебаний не зависит от амплитуды колебаний . Такое свойство маятников получило название изохронности (от греч. «изос» – равный, «хронос» – время), т.е. постоянства периода колебаний маятника вне зависимости от амплитуды колебаний.

В Пизе и по сей день показывают "лампу Галилея" - люстру, свисающую из под купола на 49-метровом подвесе.

Г. Галилей нашел соотношение между периодами маятников различной длины, используя грузики из свинца и пробки , и показал, что этот период не зависит от массы , хотя колебания маятника с грузиком из пробки затухали быстрее.

В качестве указателя времени Галилей пользовался собственным пульсом .

Галилео Галилей

( 1564 – 1642 )

Это был не только один из первых экспериментов в истории новой физики, но и изобретение нового часового механизма – Галилей предложил измерять время путем счета колебаний маятника .

Однако маятниковые часы системы Галилея были изготовлены лишь три четверти века спустя, в 1656 году Христианом Гюйгенсом (1629 — 1695), нидерландским механиком, физиком и математиком.

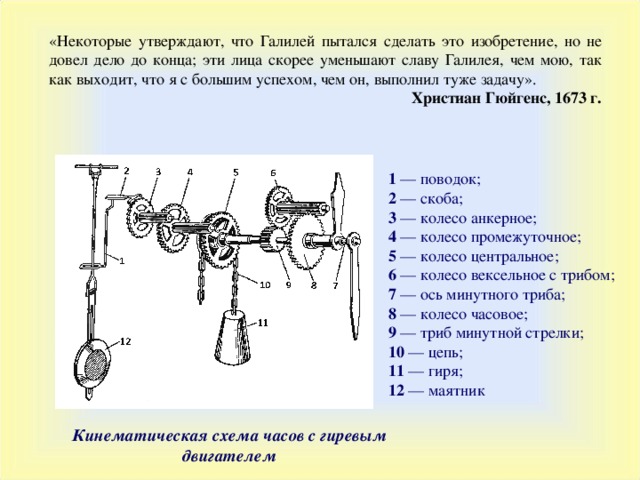
«Некоторые утверждают, что Галилей пытался сделать это изобретение, но не довел дело до конца; эти лица скорее уменьшают славу Галилея, чем мою, так как выходит, что я с большим успехом, чем он, выполнил туже задачу».

Христиан Гюйгенс, 1673 г.

1 — поводок;

2 — скоба;

3 — колесо анкерное;

4 — колесо промежуточное;

5 — колесо центральное;

6 — колесо вексельное с трибом;

7 — ось минутного триба;

8 — колесо часовое;

9 — триб минутной стрелки;

10 — цепь;

11 — гиря;

12 — маятник

Кинематическая схема часов с гиревым двигателем

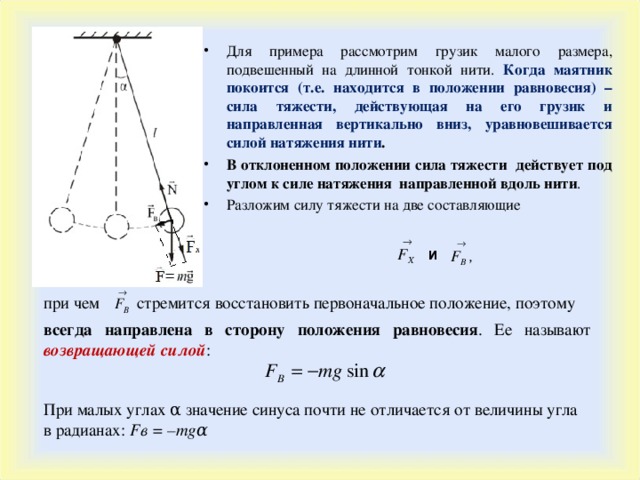
• Для примера рассмотрим грузик малого размера, подвешенный на длинной тонкой нити. Когда маятник покоится (т.е. находится в положении равновесия) – сила тяжести, действующая на его грузик и направленная вертикально вниз, уравновешивается силой натяжения нити .
• В отклоненном положении сила тяжести действует под углом к силе натяжения направленной вдоль нити .
• Разложим силу тяжести на две составляющие

и

стремится восстановить первоначальное положение, поэтому

при чем

всегда направлена в сторону положения равновесия . Ее называют возвращающей силой :

При малых углах α значение синуса почти не отличается от величины угла в радианах : F в = – mg α

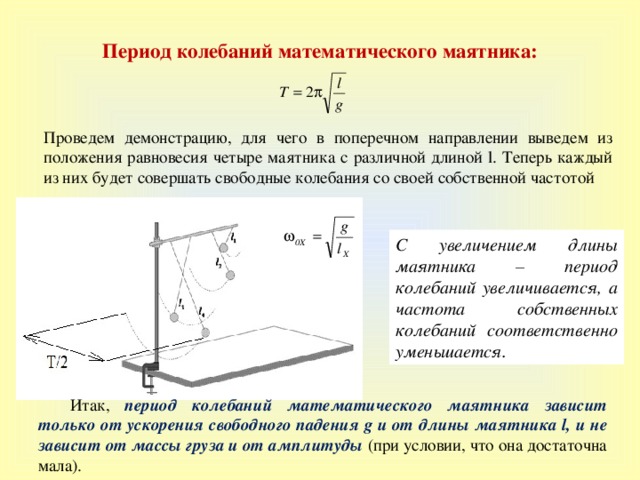
Период колебаний математического маятника :

Проведем демонстрацию, для чего в поперечном направлении выведем из положения равновесия четыре маятника с различной длиной l. Теперь каждый из них будет совершать свободные колебания со своей собственной частотой

С увеличением длины маятника – период колебаний увеличивается, а частота собственных колебаний соответственно уменьшается.

Итак, период колебаний математического маятника зависит только от ускорения свободного падения g и от длины маятника l , и не зависит от массы груза и от амплитуды (при условии, что она достаточна мала).

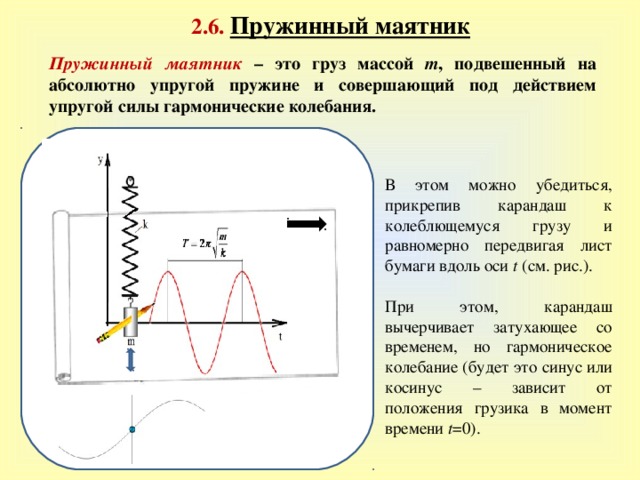
2 . 6 . Пружинный маятник

Пружинный маятник – это груз массой m , подвешенный на абсолютно упругой пружине и совершающий под действием упругой силы гармонические колебания.

В этом можно убедиться, прикрепив карандаш к колеблющемуся грузу и равномерно передвигая лист бумаги вдоль оси t (см. рис.).

При этом, карандаш вычерчивает затухающее со временем, но гармоническое колебание (будет это синус или косинус – зависит от положения грузика в момент времени t =0).

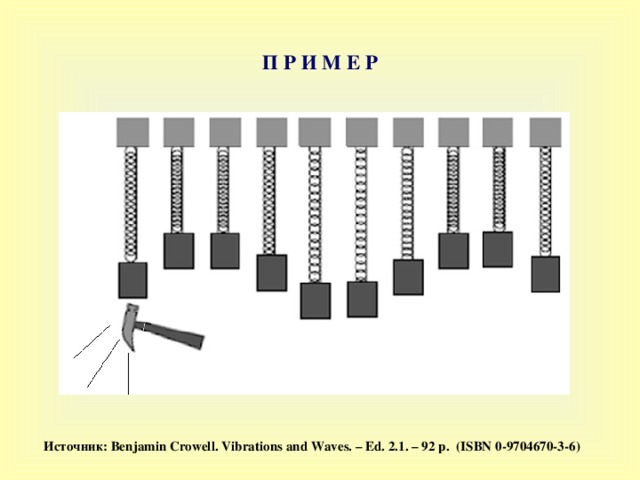
П Р И М Е Р

Источник : Benjamin Crowell. Vibrations and Waves. – Ed. 2.1. – 92 p. (ISBN 0-9704670-3-6)

Период вертикальных колебаний пружинного маятника :

Формула справедлива для упругих колебаний, при условии, что масса пружины мала по сравнению с массой груза .

Собственная частота пружинного маятника :

Собственная частота пружинного маятника будет тем выше, чем больше его упругость и меньше масса грузика . И наоборот, чем тяжелее грузик и менее упругая пружина, тем ниже частота его собственных колебаний.

У П Р О Щ Е Н И Я

При выводе формулы полагают, что : 1) пружина невесома, 2) грузик является

абсолютно жестким, т.е. деформация грузика отсутствует, 3) пренебрегают

крутильными колебаниями, которые возникают вместе с основными

2 . 7 . Дифференциальное уравнение гармонических колебаний

Рассмотрим движение горизонтального пружинного маятника. Брусок массой m расположен на гладкой горизонтальной поверхности и прикреплен к неподвижному упору с помощью пружины жесткости k .

Положение бруска будем описывать с помощью декартовой координаты x , начало отсчета которой совместим с положением, в котором пружина не деформирована. При отклонении бруска от положения равновесия на него будет действовать сила упругости пружины

направленная к положению равновесия, ее модуль определяется законом Гука

На основании II-го закона Ньютона и, пренебрегая силой трения, запишем уравнение, описывающее движение бруска:

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатой x : ускорение является второй производной координаты тела x по времени t :

обозначает вторую производную по времени t от функции x ( t ) .

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде:

Как мы знаем, отношение k/m называют собственной частотой пружинного маятника (колебательной системы) и обозначают

Откуда

Окончательно получим

Это уравнение называется дифференциальным уравнением гармонических колебаний второго порядка.

2 .8. Энергия гармонического колебания

Полная энергия гармонического колебания Е определяется суммой кинетической E K и потенциальной Е П энергии:

где

, а

Учитывая это, найдем

Полная энергия гармонического колебания не зависит от времени и прямо пропорциональна массе тела, квадрату амплитуды и квадрату частоты колебания.

2.9. Вынужденные колебания и резонанс

Колебания, происходящие под действием внешней периодической силы, называют вынужденными колебаниями .

Внешняя периодическая сила, называемая вынуждающей , сообщает колебательной системе дополнительную энергию , которая идет на восполнение энергетических потерь, например происходящих из-за трения.

П Р И М Е Р №1

Например, будем вручную перемещать вершину пружинного маятника туда-сюда. Колебания пружинного маятника, вызванные этим способом, становятся вынужденными.

П Р И М Е Р №2

Поперечные колебания балки, которая служит опорой для электродвигателя. Такие колебания возникают если у двигателя вращающиеся массы не вполне уравновешены. Период вынужденных колебаний равен периоду изменения возмущающей силы.

Источник : http://distance.net.ua/Russia/Sopromat/lekcia/razdel15/urok118.htm

СВОЙСТВА ВЫНУЖДЕННЫХ КОЛЕБАНИЙ :

• вынужденные колебания происходят с частотой внешней силы;
• амплитуда вынужденных колебаний пропорциональна амплитуде внешней силы;
• амплитуда колебаний является функцией частоты внешней силы;
• если вынуждающая сила изменяется во времени по закону синуса или косинуса, то вынужденные колебания будут гармоническими и незатухающими.

В случае, когда частота вынуждающей силы совпадает с собственной частотой колебательной системы, происходит резкое возрастание амплитуды вынужденных колебаний . Это явление называется резонансом .

Механические и акустические резонансные явления впервые описал итальянский учёный Г. Галилеем, а резонанс в электромагнитных системах (колебательный контур) английский учёный Дж. Максвелл (1868).

Примеры резонанса

1. Раскачивание ребенка на качелях.

Качели, так же как и маятник, имеют свою собственную частоту колебаний. Если бы мы подталкивали качели со случайной частотой, то качели болтались бы туда-сюда, но раскачать их сильно нам бы так и не удалось. Поэтому мы подталкиваем качели, согласуясь с их собственной частотой, а амплитуда колебаний при этом нарастает.

2. Причиной разрушения Такомского моста (штат Вашингтон, США) 7 ноября 1940 г. были отчасти механические резонансные явления: частота колебаний воздушных вихрей, вызванных сильным порывистым ураганным ветром, совпала с собственной частотой колебаний моста, возник резонанс. Амплитуда колебаний Такомского моста нарастала, до тех пор, пока многотонная конструкция не рухнула .

O брушение моста через реку Такома

( длина ~ 85 0 м )

Начиная с 8 часов утра 7 ноября наблюдались не очень сильные вертикальные многоузловые (в форме нескольких волн) изгибные колебания с частотой 0,8 Гц . Примечательно, что ветер имел не очень большую скорость − около 17 м/с , тогда как до этого были случаи, когда мост выдерживал более сильный ветер.

Около 10 часов утра скорость ветра несколько возросла (до 18,7 м/с), и установились одноузловые (в форме одной волны) изгибно-крутильные колебания со значительно меньшей частотой ( 0,2 Гц ) и весьма большими амплитудами. Когда закрутка достигала максимума, проезжая часть наклонялась к горизонту под углом 45° . Резкое изменение частоты колебаний произошло, по-видимому, вследствие обрыва каких-то важных связей в конструкции. Мост выдерживал эти колебания около часа, после чего большой участок проезжей части полотна отломился и упал в воду. Весь процесс был заснят на кинопленку, что явилось ценным материалом для исследования причин обрушения.

Видео обрушения моста : http://ru.wikipedia.org/wiki/ Файл :Tacoma_Narrows_Bridge_destruction.ogg

2.10. Автоколебания

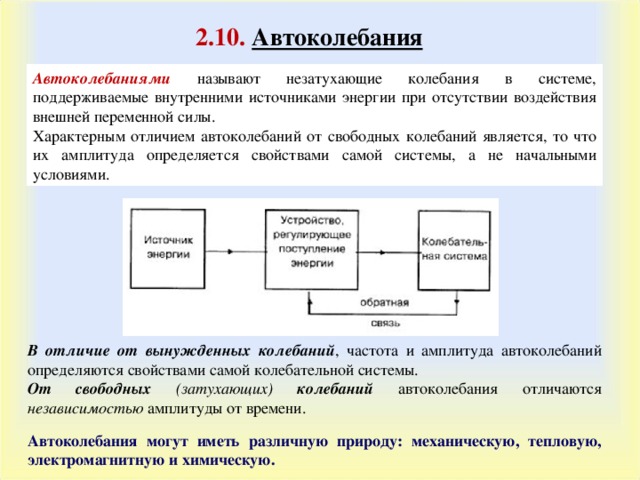
Автоколебаниями называют незатухающие колебания в системе, поддерживаемые внутренними источниками энергии при отсутствии воздействия внешней переменной силы.

Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями.

В отличие от вынужденных колебаний , частота и амплитуда автоколебаний определяются свойствами самой колебательной системы.

От свободных (затухающих) колебаний автоколебания отличаются независимостью амплитуды от времени.

Автоколебания могут иметь различную природу: механическую, тепловую, электромагнитную и химическую.

Примеры автоколебательных систем

1. Пример механической автоколебательной системы – часовой механизм с анкерным ходом .

На ось ходового колеса действует постоянный момент силы M , передающийся через зубчатую передачу от заводной пружины или от гири. При вращении колеса его зубцы сообщают кратковременные импульсы силы маятнику (осциллятору), благодаря которым его колебания не затухают. Кинематика механизма играет роль обратной связи в системе, синхронизируя вращение колеса с колебаниями маятника таким образом, что за полный период колебания колесо поворачивается на угол, соответствующий одному зубцу.

2. Электрические или электромагнитные автоколебания образуются в генераторах электрических сигналов, используемых в радио, телевидении, компьютерах, а также в оптических квантовых генераторах – лазерах.

3 . А втоколебания присущи не только неживой природе. В живой природе они происходят как на уровне организма - биение сердца, периодическое непроизвольное сокращение мышц и т.д., так и на более высоком уровне, например на уровне биогеоценоза.

Еще в 1729 году француз де Меран обратил внимание на то, что ночью листья растений совершают колебательные движения.

Для большинства биологических систем характерны автоколебания различных характеристик. Период этих колебаний может быть связан с периодическими изменениями условий жизни на Земле  смены времен года, смены дня и ночи. Существуют и другие геофизические ритмы – солнечные, лунные, связанные с атмосферными явлениями.

Периодическое изменение показателей жизнедеятельности человека в результате автоколебаний называют биоритмами .

2.11. Классификация колебаний

ПО ФИЗИЧЕСКОЙ ПРИРОДЕ

БИОЛОГИЧЕСКИЕ

• колебания показателей

жизнедеятельности

живых систем на всех

уровнях их организации

ЭЛЕКТРОМАГНИТНЫЕ

• колебания электрических

и магнитных характеристик

МЕХАНИЧЕСКИЕ

• смещение тела или

точек сплошной

упругой среды вблизи

положения равновесия

(в т.ч. звук)

СМЕШАННОГО ТИПА

- комбинации вышеперечисленных

ПО ТИПУ ВОЗВРАЩАЮЩЕЙ СИЛЫ К ПОЛОЖЕНИЮ

РАВНОВЕСИЯ КОЛЕБЛЮЩЕЙСЯ СИСТЕМЫ

СВОБОДНЫЕ

ВЫНУЖДЕННЫЕ

• совершаются под действием внутренних сил

• совершаются под действием внешней силы

АВТОКОЛЕБАНИЯ

• система имеет запас потенциальной энергии, которая и расходуется на совершение колебаний

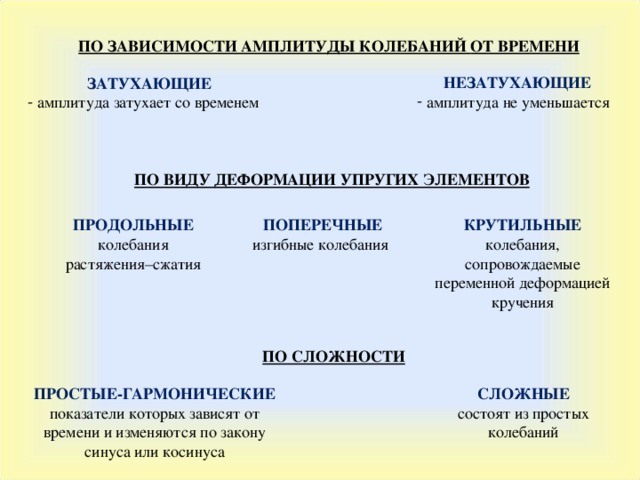
ПО ЗАВИСИМОСТИ АМПЛИТУДЫ КОЛЕБАНИЙ ОТ ВРЕМЕНИ

НЕЗАТУХАЮЩИЕ

• амплитуда не уменьшается

ЗАТУХАЮЩИ Е

• амплитуда затухает со временем

ПО ВИДУ ДЕФОРМАЦИИ УПРУГИХ ЭЛЕМЕНТОВ

ПРОДОЛЬНЫЕ

КРУТИЛЬНЫЕ

ПОПЕРЕЧНЫЕ

изгибные колебания

колебания растяжения–сжатия

колебания, сопровождаемые переменной деформацией кручения

ПО СЛОЖНОСТИ

ПРОСТЫЕ-ГАРМОНИЧЕСКИЕ

СЛОЖНЫЕ

состоят из простых колебаний

показатели которых зависят от времени и изменяются по закону синуса или косинуса

Источники

• Воронкин А.С. Линейные колебания и волны: Введение в акустику : уч. пособ. А. С. Воронкин. – Луганск : СПД Рєзніков В.С., 2012. – 224 с.
• Боровой А. Колебания и маятники / A . Боровой, A . Херувимов // Научно-популярный физико-математический журнал «Квант», 1981. – №8. – С. 30–33.
• Воронкин А. С. Введение в физику звука / А. С. Воронкин. – Луганск : Изд-во ЛГИКИ, 2012. – 96 с.
• Джанколи Д. Физика : в 2 т. / Д. Джанколи ; [пер. с англ. А. Добраславского, М. Котельниковой и М. Суханова]. – Т. 1. – М. : Мир, 1989. – 656 с.
• Засєкіна Т. М. Фізика : підручник для 10 кл. загальноосвіт. навч. закл. (профільний рівень) / Т. М. Засєкіна, В. М. Головко. – К. : Педагогічна думка, 2010. – 304 с.
• Мандельштам Л. И. Лекции по теории колебаний / Л. И. Мандельштам. − М. : Наука, 1972. − 470 с.
• Михайлов А. Волны в сердце / А. Михайлов // Научно-популярный физико-математический журнал «Квант», 1987. – № 9. – C . 9–14.

• Можаев В. Колебания / В. Можаев // Научно-популярный физико-математический журнал «Квант», 1981. – № 3. – С. 46–50.
• Мякишев Г. Я. Физика: Колебания и волны. 11 кл. / Г. Я. Мякишев, А. 3. Синяков. – М. : Дрофа, 2002. – 288 с.
• Пиппард А. Физика колебаний / А. Пиппард. – М. : Высшая школа,1985. – 456 с.
• Овчинников А. Об амплитудах колеблющихся величин / А. Овчинников, В. Плис // Научно-популярный физико-математический журнал «Квант», 1999. – № 1. – С. 46–49.
• Яворский Б. М. Основы физики. Колебания и волны. Квантовая физика. Физика ядра и элементарных частиц / Б. М. Яворский, А. А. Пинский. – М. : ФИЗМАТЛИТ, 2003. – Т. 2. – 550 с.
• Интернет-ресурсы