ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЁЖНОЙ ПОЛИТИКИ ВОРОНЕЖСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВОРОНЕЖСКОЙ ОБЛАСТИ
«Воронежский техникум строительных технологий»
(ГБПОУ ВО «ВТСТ»)
МЕТОДИЧЕСКОЕ ПОСОБИЕ
по дисциплине
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Воронеж
2019
ОДОБРЕНО
Предметной (цикловой) комиссией
естественнонаучных дисциплин
Протокол заседания № ______
от «_____» __________ 2019 г.
Председатель П(Ц)К
________________ / Болычева А.В. /
Настоящее пособие предназначено для студентов 2 курса ГБПОУ ВО «Воронежский техникум строительных технологий» специальностей «Информационные системы (по отраслям)» и «Прикладная информатика (по отраслям)» и полностью соответствует программе по математике для СПО. Оно может быть использовано студентами для самостоятельного изучения раздела программы, а также преподавателем на уроке при изучении нового материала, для домашнего задания, при повторении и подготовке к зачётной работе.
Пособие включает в себя, помимо задач, теоретические сведения, необходимые для решения задач раздела «Линейная алгебра», подробные решения типовых примеров, вопросы для самопроверки, а также упражнения для самостоятельного решения.
Автор - составитель: Сафонова Елена Артуровна, преподаватель ГБПОУ ВО
«Воронежский техникум строительных технологий»
СОДЕРЖАНИЕ
Введениеч 3
 Определение матрицы. Действия над матрицами. 4
Определение матрицы. Действия над матрицами. 4
1. Матрицы 4
2. Виды матриц 4
3. Равенство матриц 5
4. Линейные операции над матрицами 5
5. Умножение матриц 6
 Определитель матрицы. Свойства определителей и их вычисление 8
Определитель матрицы. Свойства определителей и их вычисление 8
1. Определитель матрицы. Вычисление определителей второго и третьего порядков 8
2. Основные свойства определителей 9
3. Миноры и алгебраические дополнения элементов определителя 10
4. Вычисление определителя разложением по элементам строки или столбца 11
 3. Обратная матрица. Обращение матриц второго и третьего порядков 12
3. Обратная матрица. Обращение матриц второго и третьего порядков 12
1. Определение обратной матрицы 12
2. Вычисление обратных матриц второго и третьего порядков 13
§ 4. Решение простейших матричных уравнений 14
Вопросы и задачи по теме 16
Литература 17
Термин « матрица » имеет много значений. Например, в математике матрицей называется система элементов, имеющая вид прямоугольной таблицы, в программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Покерные фишки также имеют непосредственное отношение к матрице. Фишки для покера изготавливаются из высококачественного композиционного материала, зачастую с металлической сердцевиной. В свою очередь композиционный материал или композит имеет матрицу и включенные в нее армирующие элементы (исключение составляют слоистые композиты).
Матрица в фотографии – это интегральная микросхема (аналоговая или цифро-аналоговая), которая состоит из фотодиодов (светочувствительных элементов). Благодаря светочувствительной матрице происходит преобразование спроецированного на нее оптического изображения в электрический сигнал аналогового типа, а при наличии в составе матрицы АЦП, то преобразование происходит в поток цифровых данных.
Матрица – основной элемент цифровых фотоаппаратов, всех современных видео- и телекамер, фотокамер, встроенных в мобильный телефон и системы видеонаблюдения.
Основное значение термин «матрица» имеет в математике.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи. Одним из способов решения систем линейных уравнений являются определители, которые составляются из матриц.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
 Определение матрицы. Действия над матрицами. 1. Матрицы
Определение матрицы. Действия над матрицами. 1. Матрицы Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк n столбцов. Для записи матрицы используется следующее обозначение:
 Сокращённо прямоугольную матрицу типа
Сокращённо прямоугольную матрицу типа 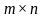 можно записать так: A = (
можно записать так: A = (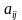 ). Любой элемент матрицы обозначается
). Любой элемент матрицы обозначается 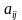 , где i - номер строки, j - номер столбца.
, где i - номер строки, j - номер столбца.
Если число строк матрицы не равно числу столбцов 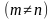 , то матрица называется прямоугольной. Таковы, например, матрицы:
, то матрица называется прямоугольной. Таковы, например, матрицы:
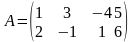 - матрица типа
- матрица типа  ,
, 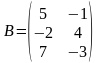 - матрица типа
- матрица типа 
Если число строк равно числу столбцов 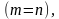 то матрица называется квадратной. Например,
то матрица называется квадратной. Например, 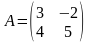
Число строк или столбцов квадратной матрицы называется её порядком. Например, порядок квадратной матрицы 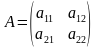 равен 2.
равен 2.
Рассмотрим квадратную матрицу порядка n: 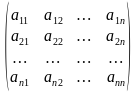 .
.
Диагональ, содержащую элементы 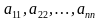 , будем называть главной, а диагональ, содержащую элементы
, будем называть главной, а диагональ, содержащую элементы 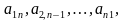 - побочной.
- побочной.
Среди квадратных матриц выделим матрицы, у которых не равны нулю только элементы, находящиеся на главной диагонали, например: 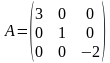 . Такие матрицы называются диагональными.
. Такие матрицы называются диагональными.
Если у диагональной матрицы все числа главной диагонали равны между собой, то такая диагональная матрица называется скалярной. Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е: 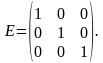
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается так: 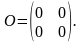
В прямоугольной матрице типа 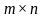 возможен случай, когда
возможен случай, когда 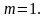 При этом получается матрица-строка:
При этом получается матрица-строка: 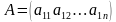 . В случае, когда
. В случае, когда получаем матрицу-столбец: .
Две матрицы называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны:
Так, матрицы
и
равны, если
Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа 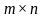 , либо квадратные одного и того же порядка n.
, либо квадратные одного и того же порядка n.
Если в матрице типа 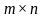 переставить строки со столбцами, получим матрицу типа
переставить строки со столбцами, получим матрицу типа , которую называют транспонированной и обозначают
.
Например,
и
Суммой матриц А и В будем называть такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В .
Складывать можно только матрицы, имеющие одинаковое строение : или прямоугольные типа m×n, или квадратные одинакового порядка.
1. Сложить матрицы А и В, если
а) , .
Р е ш е н и е. Здесь А и В – квадратные матрицы второго порядка. Складывая их соответствующие элементы, получим
б) ,
Р е ш е н и е. Здесь А и В – прямоугольные матрицы типа . Складываем их соответствующие элементы:
в) , .
Р е ш е н и е. Эти прямоугольные матрицы сложить нельзя, так как есть матрица типа
, а можно складывать только прямоугольные матрицы одного типа.
2 - 4. Сложить матрицы А и В:
2. , .
3. , .
4. ,
На сложение матриц распространяются важнейшие свойства чисел:
1) переместительный закон: где
- либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа
2) сочетательный закон сложения , где
- либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного типа
 .
.
Произведением матрицы на число k называется такая матрица kA, каждый элемент которой равен
, то есть чтобы умножить матрицу
на число
нужно все элементы матрицы умножить на это число.
5. Умножить матрицу на число .
Р е ш е н и е. Умножая каждый элемент матрицы А на 3, получим
3A = = .
6. Найти линейную комбинацию если
,
Р е ш е н и е. Сначала находим произведения А на и
на
.
Теперь найдём сумму полученных матриц:
.
7 - 9. Вычислить линейные комбинации матриц:
7. если
8. , если , .
9. , если
Рассмотрим умножение квадратных матриц второго порядка. Пусть
А = и В =
Произведением этих матриц называется матрица
.
10. Найти произведение матриц A и В, если
Р е ш е н и е.
11 – 13. Найти произведения матриц:
11.
12.
13. .
Правило нахождения матрицы – произведения распространяется на умножение и прямоугольных матриц.
14.
Для прямоугольных матриц справедливы следующие правила:
1) умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.
15 – 18. Найти произведение АВ:
15.
16.
17.
18. .
19. Вычислить где .
20. Найти где
.
21. Найти если
22. Найти AE, если
6. Свойства умножения матриц
1) Произведение двух матриц не подчиняется переместительному закону, то есть .
2) Сочетательный закон:
3) Распределительный закон
Известно, что произведение двух отличных от нуля чисел не равно нулю. Для матриц это не всегда справедливо, т.е. возможен случай, когда произведение двух ненулевых матриц может оказаться равным нулевой матрице. Например, если
то
 Определитель матрицы. Свойства определителей и их вычисление
Определитель матрицы. Свойства определителей и их вычисление
Пусть дана квадратная матрица второго порядка: 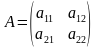 .
.
Определителем второго порядка, соответствующим данной матрице, называется число
Определитель второго порядка записывается так:
Элементы
образуют главную диагональ определителя,
– побочную. Вычисление определителя 2-го порядка иллюстрируется схемой:
то есть из произведения элементов главной диагонали вычитается произведение элементов побочной.
23. Вычислить определители второго порядка:
а) б)
Р е ш е н и е. а)
б)
24 - 30 . Вычислить определители:
24. 25.
26.
27.
;
28. 29.
30.
Пусть дана квадратная матрица третьего порядка .
Определителем третьего порядка, соответствующим данной матрице, называется число ,
Определитель третьего порядка записывается так:
При вычислении определителей третьего порядка удобно пользоваться правилом треугольников. Это правило проиллюстрируем по схеме:
Определитель 3-го порядка представляет собой алгебраическую сумму шести произведений, причем три произведения берутся со знаком „ + “ и три – со знаком „ – “. Со знаком „ + “ берется произведение элементов, стоящих на главной диагонали, а также произведения элементов, стоящих на параллели к главной диагонали, с добавлением третьего множителя из противоположного угла таблицы. Со знаком „ – “ берется произведение элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на параллели к побочной диагонали, с добавлением третьего множителя из противоположного угла таблицы.
31. Вычислить определитель третьего порядка.
32 – 39. Вычислить определители:
32. . 33. 34.
35. 38. 39.
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (т.е. транспонировать), и наоборот.
Пример:
Это свойство называется свойством равноправности строк и столбцов.
2. При перестановке двух строк (или столбцов) определитель меняет знак на противоположный:
Пример:
Поменяв местами столбцы, получим
3. Определитель, имеющий две одинаковых строки (или столбца) равен нулю.
Пример:
4. Общий множитель элементов какого-либо строки (или столбца) определителя можно вынести за знак определителя:
.
Пример:
5. Если все элементы некоторой строки (или столбца) пропорциональны соответствующим элементам другой строки (или столбца), то такой определитель равен 0.
Пример:
6. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины:
7. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали:
3. Миноры и алгебраические дополнения элементов определителя
Минором элемента
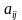 определителя D = |
определителя D = |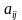 |, называют такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащий данный элемент.
|, называют такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащий данный элемент.
Например, минор М23, соответствующий элементу определителя
получается, если вычеркнуть из определителя D вторую строку и третий столбец, т.е.
40 - 41. Записать все миноры определителя:
40. .
Ре ш е н и е.
41. а)
Алгебраическим дополнением элемента
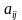 определителя D называется минор
определителя D называется минор этого элемента, взятый со знаком
. Алгебраическое дополнение элемента
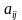 обозначается
обозначается .
Таким образом, .
42. Вычислить алгебраические дополнения элементов определителя
Ре ш е н и е.
43. Найти алгебраические дополнения элементов определителя
Теорема. Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т.е.
D = +
+ … +
или D =
.
…
.
Эти соотношения называют разложением определителя по элементам -й строки или -го столбца.
44. Вычислить определитель разложением:
а) по элементам 2-ой строки; б) по элементам 1-го столбца.
Р е ш е н и е.
б)
Если определитель имеет четвёртый или более высокий порядок, то его также можно разложить по элементам строки или столбца, а затем понижать порядок алгебраических дополнений.
45. Вычислить определитель
.
Р е ш е н и е. Разложим определитель по элементам 1-ой строки (так как она содержит два нулевых элемента):
Поскольку второй и четвёртый члены разложения равны нулю, имеем
46 – 48. Вычислить определители третьего порядка:
46. . 47.
. 48. .
49 – 51. Вычислить определители четвёртого порядка:
49. . 50. 51.
Перечислим различные способы вычисления определителей.
1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители второго и третьего порядков, а для определителя более высокого порядка применим следующий способ.
2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.
3. Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 7 треугольный определитель равен произведению элементов главной диагонали.
Чтобы получить треугольный определитель, нужно, используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор пока не придём к определителю треугольного вида.
Пусть, например, требуется вычислить определитель
.
Вычитая первую строку из всех остальных, сразу получим определитель треугольного вида:
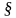 3. Обратная матрица. Обращение матриц второго и третьего порядков 1. Определение обратной матрицы
3. Обратная матрица. Обращение матриц второго и третьего порядков 1. Определение обратной матрицы Квадратная матрица называется вырожденной, если её определитель равен нулю, и невырожденной, если её определитель не равен нулю.
Если – квадратная матрица, то обратной по отношению к
называется матрица, которая, будучи умноженной на
, даёт единичную матрицу.
Обозначив обратную матрицу через запишем
Если обратная матрица существует, то матрица
называется обратимой. Операция нахождения обратной матрицы при условии, что она существует называется обращением матрицы. Нахождение обратной матрицы имеет большое значение при решении систем линейных уравнений и в вычислительных методах линейного программирования.
Теорема. Для того чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы матрица
была невырожденной, т.е. чтобы её определитель был отличен от нуля.
Для нахождения обратной матрицы используют следующую схему:
1. Найти определитель матрицы .
2. Найти алгебраические дополнения всех элементов 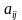 матрицы
матрицы и записать новую матрицу.
3. Поменять местами столбцы полученной матрицы (транспонировать).
4. Умножить полученную матрицу на .
52. Найти матрицу, обратную матрице
Р е ш е н и е. 1. Найдём определитель матрицы
.
Так как , то данная матрица является невырожденной и, следовательно, существует обратная матрица.
2. Найдём алгебраические дополнения каждого элемента:
Тогда получим матрицу: .
3. Транспонируем эту матрицу: .
4. Умножим полученную матрицу на , т.е.на
Проверим полученный ответ. Выполнив умножение , находим
53. Найти матрицу, обратную матрице
Р е ш е н и е. 1. Находим определитель матрицы
Поскольку , матрица
является невырожденной и, значит, можно найти матрицу
.
2. Найдём алгебраические дополнения всех элементов матрицы .
.
Запишем новую матрицу: .
3. Транспонируем полученную матрицу:
4. Умножив полученную матрицу на , находим
.
Проверим полученный ответ. Имеем
54 – 60. Найти матрицы, обратные заданной матрице А:
54. 55.
56.
57.
58. 59. 60.
§ 4. Решение простейших матричных уравнений
Пусть дана система уравнений
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
Свободные члены и неизвестные можно записать при помощи матриц-столбцов:
Тогда эту систему уравнений можно записать так:
или
Это равенство называется простейшим матричным уравнением.
Такое уравнение решается следующим образом. Пусть матрица А - невырожденная тогда существует обратная матрица
Умножив обе части матричного уравнения на обратную матрицу
, получим
Используя сочетательный закон умножения, перепишем это равенство в виде
.
Поскольку и
находим
.
Чтобы решить матричное уравнение нужно:
1. Найти обратную матрицу А-1
2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т.е.
3. Пользуясь определением равных матриц записать ответ.
61. Решить матричное уравнение .
Р е ш е н и е. 1. Будем искать обратную матрицу .
Найдём определитель матрицы
Вычислим алгебраические дополнения каждого элемента матрицы :
Запишем новую матрицу и транспонируем её .
Учитывая, что , запишем обратную матрицу
2. Умножим матрицу на матрицу
.
3. Так как , то по определению равных матриц
62 – 65. Решить матричные уравнения:
62. 63.
64. 65.
Что называется матрицей?
2. Что называется матрицей-строкой? матрицей-столбцом?
3. Какие матрицы называются прямоугольными? квадратными?
4. Какие матрицы называются равными?
5. Что называется главной диагональю матрицы?
6. Какая матрица называются диагональной?
7. Какая матрица называется единичной?
8. Какая матрица называется треугольной?
9. Что значит «транспонировать» матрицу?
10. Транспонируйте матрицу
11. Что называется суммой матриц?
12. Сложите матрицы
и .
13. Что называется произведением матрицы на число?
14. Как найти произведение двух матриц?
15. В чём состоит обязательное условие существования произведения матриц?
16. Найдите произведение матриц:
а) б) .
17. Какими свойствами обладает произведение матриц?
18. Что называется определителем матрицы?
19. Как вычислить определитель третьего порядка по схеме треугольников?
20. Что называется минором?
21. Что называется алгебраическим дополнением элемента определителя?
22. Как разложить определитель по элементам строки или столбца?
23. Какие способы вычисления определителя вам известны?
24. Перечислите свойства определителей.
25. Какая матрица называется невырожденной?
26. Какая матрица называется обратной по отношению к данной?
27. Каков порядок вычисления обратной матрицы?
28. Вычислите обратную матрицу для
29. Как записать простейшее матричное уравнение?
30. Как решить матричное уравнение?
31. Решите матричным способом систему уравнений
Ответы
10. 12. 16. а) б) 28.
31.
Богомолов Н.В. Самойленко П.И. Математика: Учебник. - М.: Дрофа, 2010.
Дадаян А.А. Сборник задач по математике. Учебное пособие. Гриф МО РФ, – М.: ФОРУМ: ИНФРА – М, 2013.
Зимина О.В. Линейная алгебра и аналитическая геометрия. Учебный комплекс М.: Издательство МЭИ.2006.
Лисичкин В.Т., Соловейчик Л.И. Математика в задачах с решениями: Учебное пособие. 3-е изд., стер. – СПб: Издательство «Лань», 2011. -464 с.: ил. – (Учебники для вузов. Специальная литература)

 Получите свидетельство
Получите свидетельство Вход
Вход











 Матрицы и определители (106.62 KB)
Матрицы и определители (106.62 KB)
 0
0 1120
1120 86
86 Нравится
0
Нравится
0







